hello-algo/docs/chapter_graph/graph.md

comments
true

图

「图 Graph」是一种非线性数据结构，由「顶点 Vertex」和「边 Edge」组成。我们可将图 G 抽象地表示为一组顶点 V 和一组边 E 的集合。例如，以下表示一个包含 5 个顶点和 7 条边的图

$$ \begin{aligned} V & = { 1, 2, 3, 4, 5 } \newline E & = { (1,2), (1,3), (1,5), (2,3), (2,4), (2,5), (4,5) } \newline G & = { V, E } \newline \end{aligned}

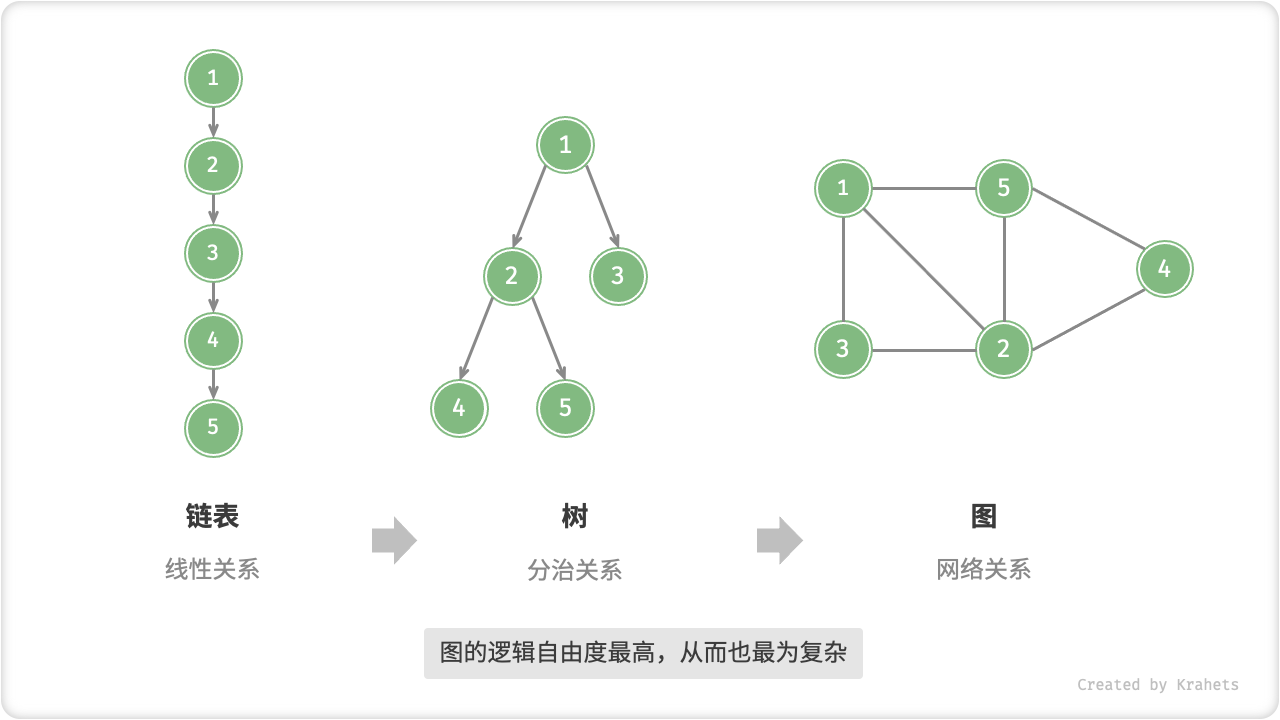
那么，图与其他数据结构的关系是什么？如果我们把「顶点」看作结点，把「边」看作连接各个结点的指针，则可将「图」看成一种从「链表」拓展而来的数据结构。相比线性关系（链表）和分治关系（树），网络关系（图）的自由度更高，也从而更为复杂。

图常见类型

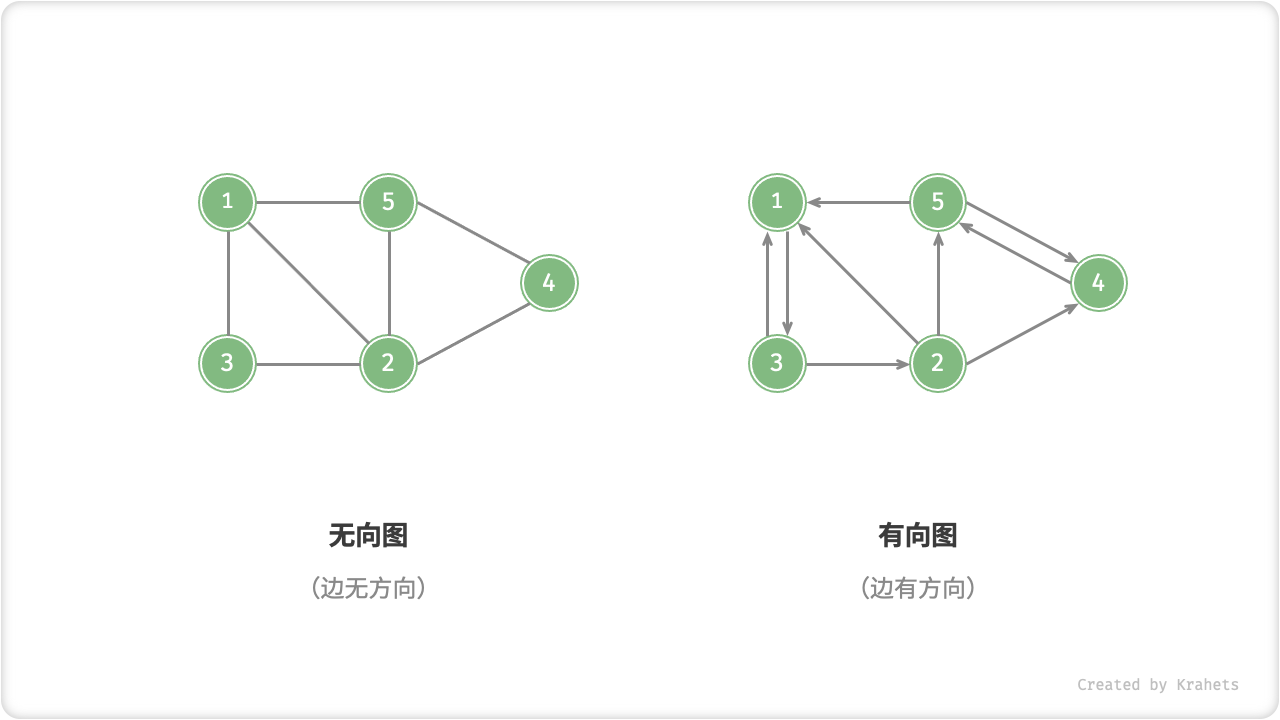
根据边是否有方向，分为「无向图 Undirected Graph」和「有向图 Directed Graph」。

• 在无向图中，边表示两结点之间“双向”的连接关系，例如微信或 QQ 中的“好友关系”；
• 在有向图中，边是有方向的，即 A \rightarrow B 和 A \leftarrow B 两个方向的边是相互独立的，例如微博或抖音上的“关注”与“被关注”关系；

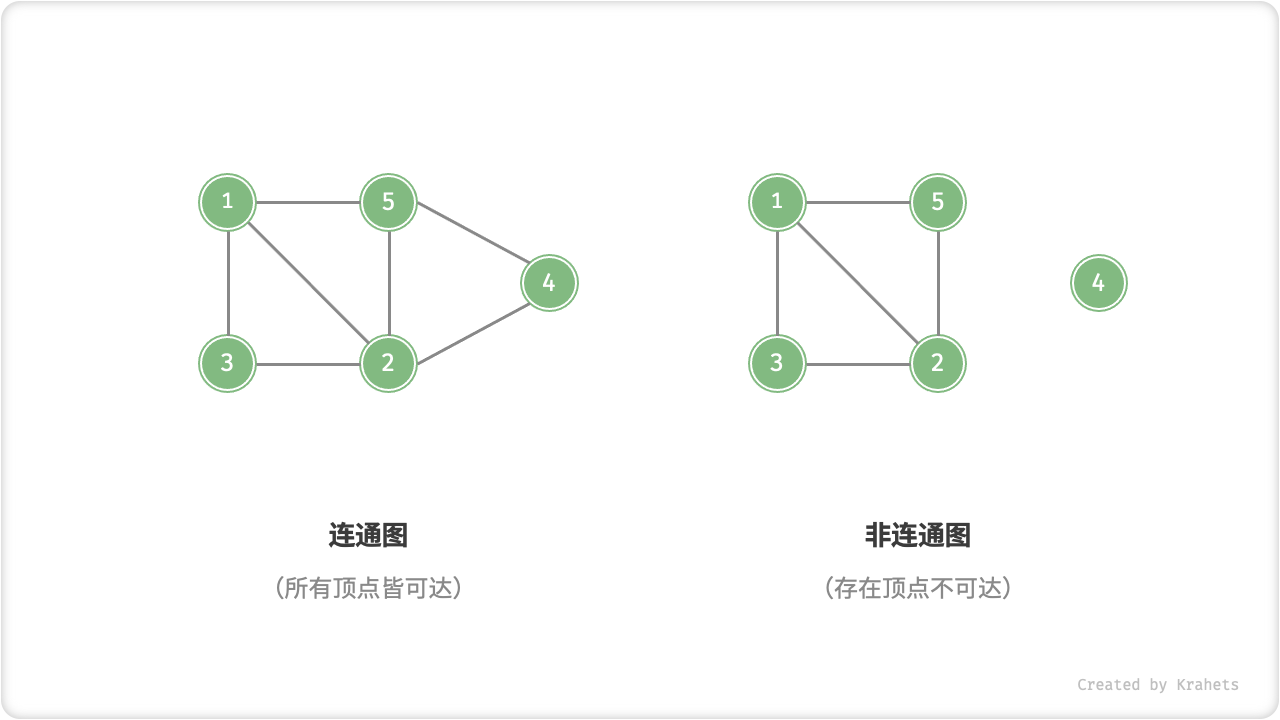
根据所有顶点是否连通，分为「连通图 Connected Graph」和「非连通图 Disconnected Graph」。

• 对于连通图，从某个结点出发，可以到达其余任意结点；
• 对于非连通图，从某个结点出发，至少有一个结点无法到达；

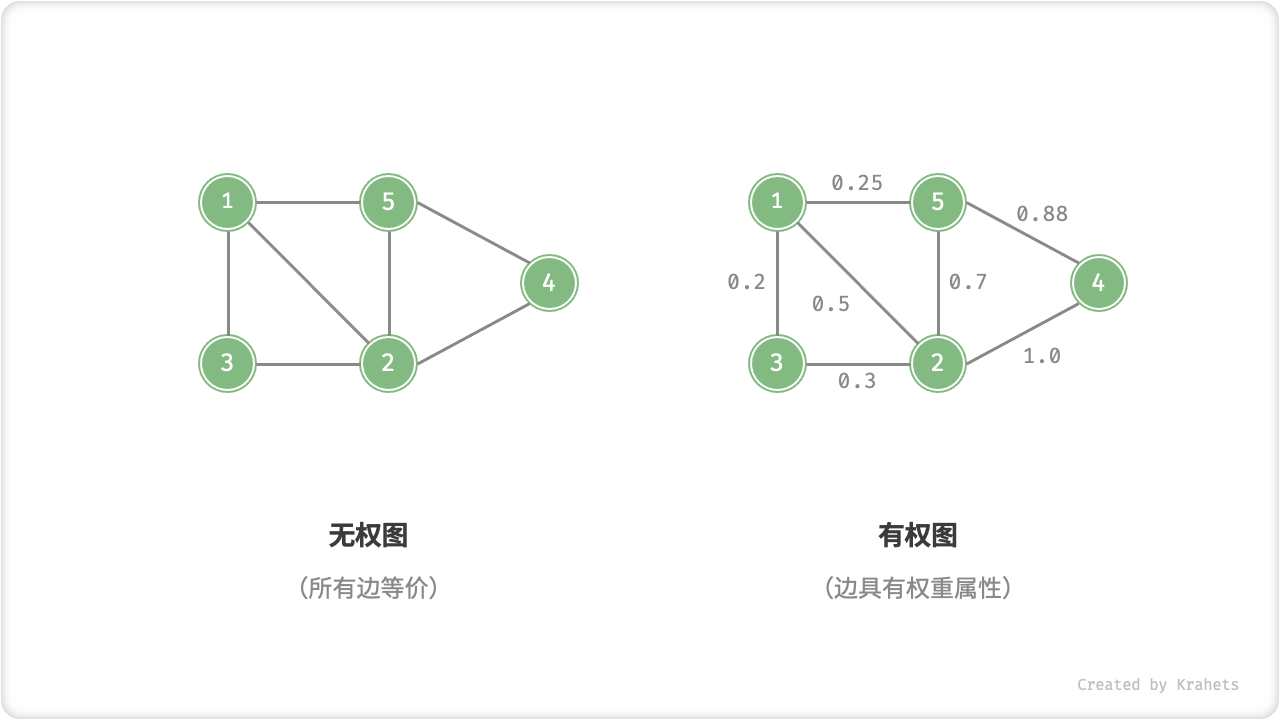
我们可以给边添加“权重”变量，得到「有权图 Weighted Graph」。例如，在王者荣耀等游戏中，系统会根据共同游戏时间来计算玩家之间的“亲密度”，这种亲密度网络就可以使用有权图来表示。

图常用术语

• 「邻接 Adjacency」：当两顶点之间有边相连时，称此两顶点“邻接”。
• 「路径 Path」：从顶点 A 到顶点 B 走过的边构成的序列，被称为从 A 到 B 的“路径”。
• 「度 Degree」表示一个顶点具有多少条边。对于有向图，「入度 In-Degree」表示有多少条边指向该顶点，「出度 Out-Degree」表示有多少条边从该顶点指出。

图的表示

图的常用表示方法有「邻接矩阵」和「邻接表」。以下使用「无向图」来举例。

邻接矩阵

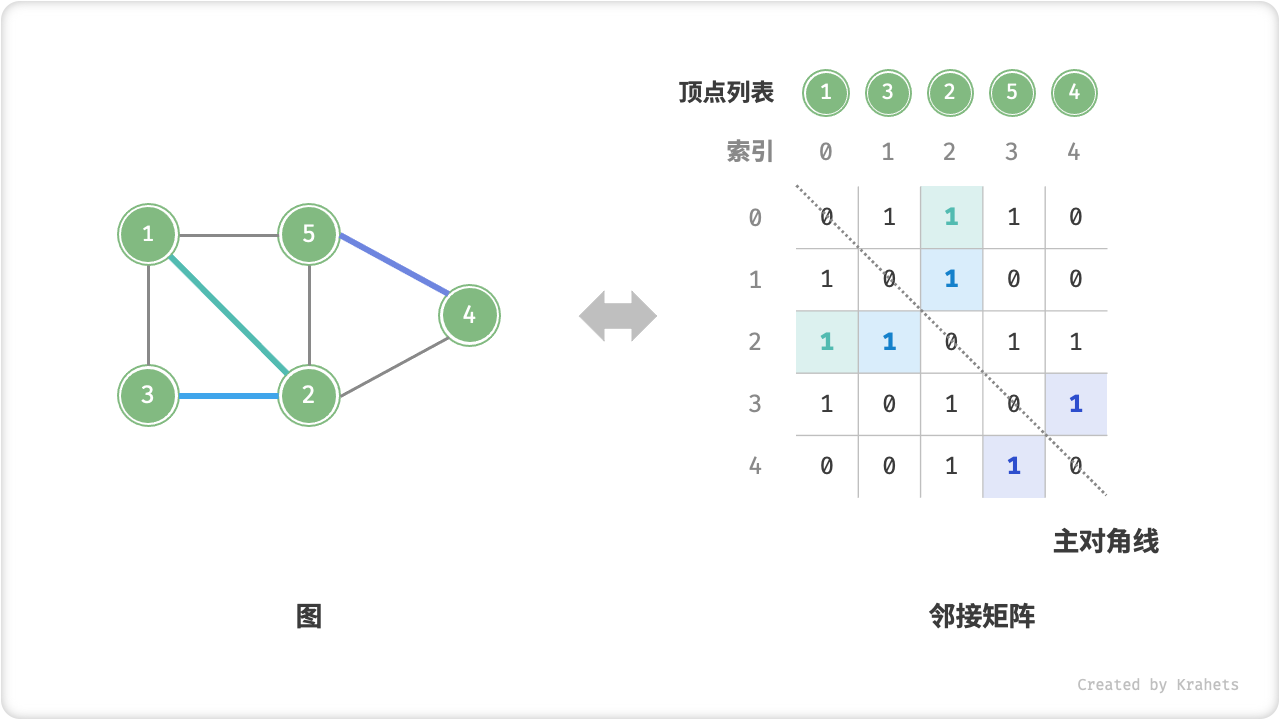
设图的顶点数量为 n ，「邻接矩阵 Adjacency Matrix」使用一个 n \times n 大小的矩阵来表示图，每一行（列）代表一个顶点，矩阵元素代表边，使用 1 或 0 来表示两个顶点之间有边或无边。

邻接矩阵具有以下性质：

• 顶点不能与自身相连，因而邻接矩阵主对角线元素没有意义。
• 「无向图」两个方向的边等价，此时邻接矩阵关于主对角线对称。
• 将邻接矩阵的元素从 1 , 0 替换为权重，则能够表示「有权图」。

使用邻接矩阵表示图时，我们可以直接通过访问矩阵元素来获取边，因此增删查操作的效率很高，时间复杂度均为 O(1) 。然而，矩阵的空间复杂度为 O(n^2) ，内存占用较大。

邻接表

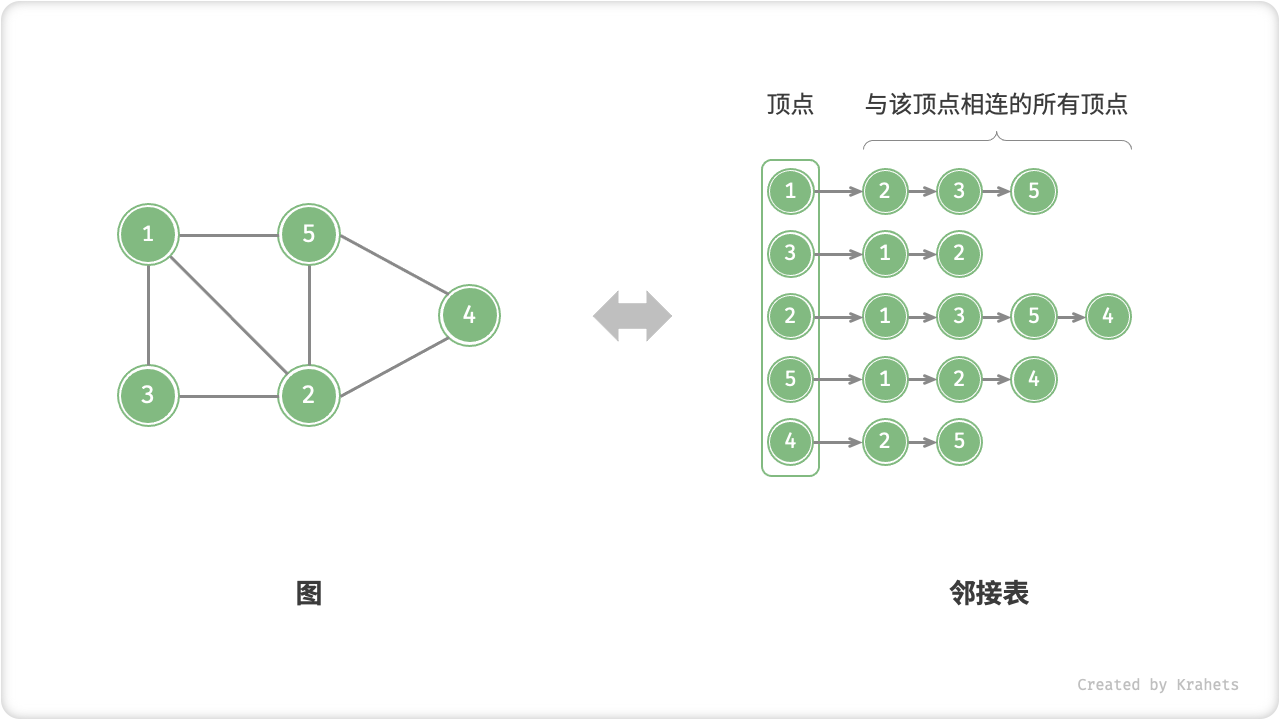
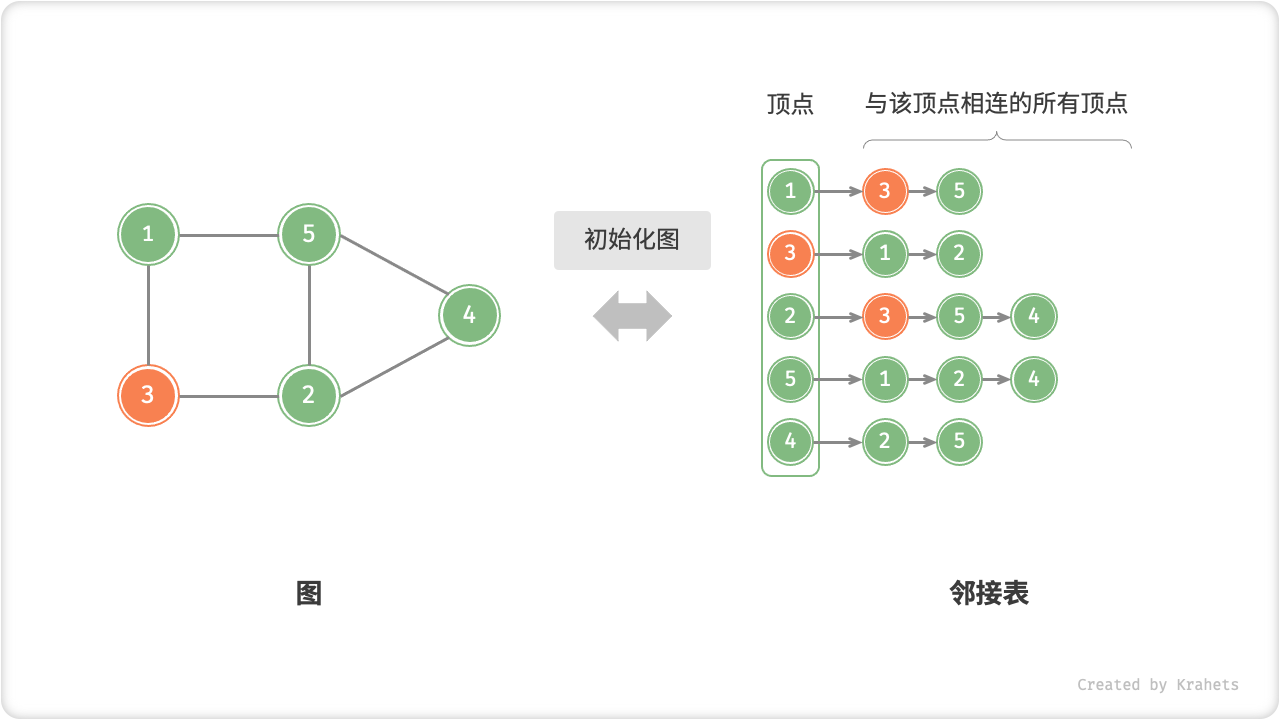
「邻接表 Adjacency List」使用 n 个链表来表示图，链表结点表示顶点。第 i 条链表对应顶点 i ，其中存储了所有与该顶点相连的顶点。

邻接表仅存储存在的边，而边的总数往往远小于 n^2 ，因此更加节省空间。但是，因为在邻接表中需要通过遍历链表来查找边，所以其时间效率不如邻接矩阵。

观察上图发现，邻接表结构与哈希表「链地址法」非常相似，因此我们也可以用类似方法来优化效率。比如，当链表较长时，可以把链表转化为「AVL 树」，从而将时间效率从 O(n) 优化至 O(\log n) ，还可以通过中序遍历获取有序序列；还可以将链表转化为 HashSet（即哈希表），将时间复杂度降低至 O(1) ，。

图基础操作

以下分别介绍图在「邻接矩阵」和「邻接表」表示下的基础操作。

基于邻接矩阵的实现

设图的顶点总数为 n ，则有：

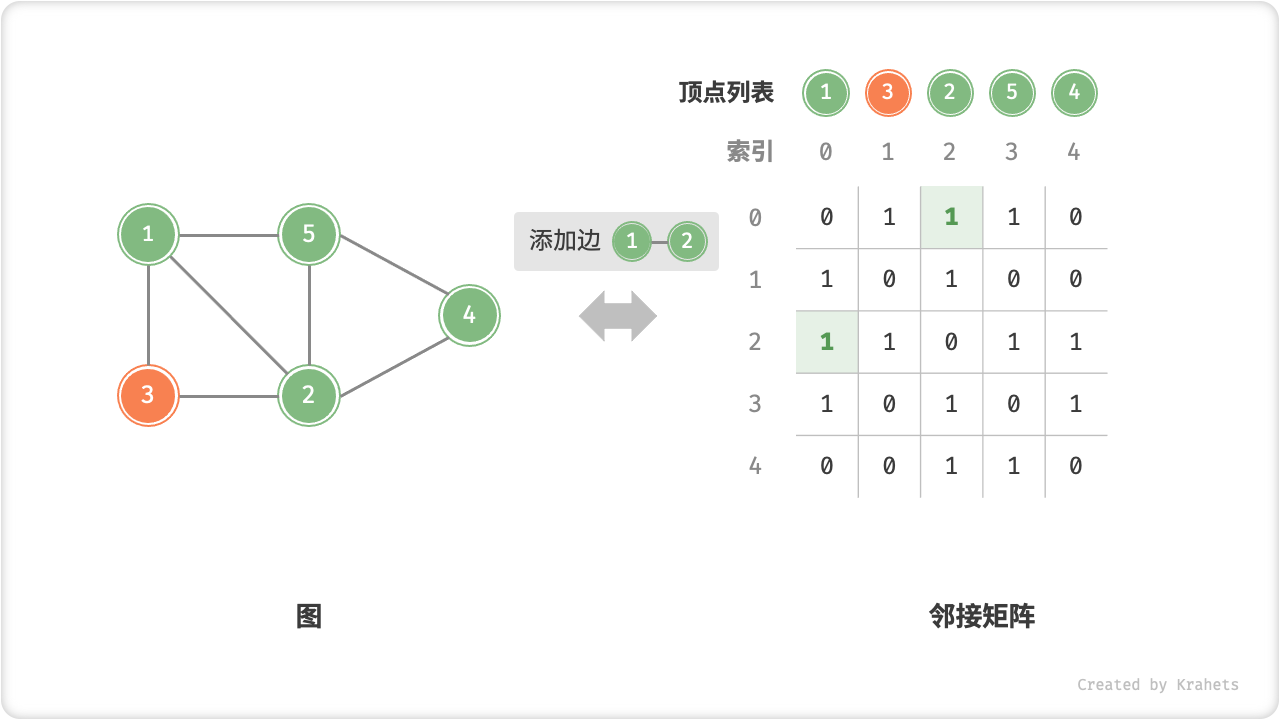
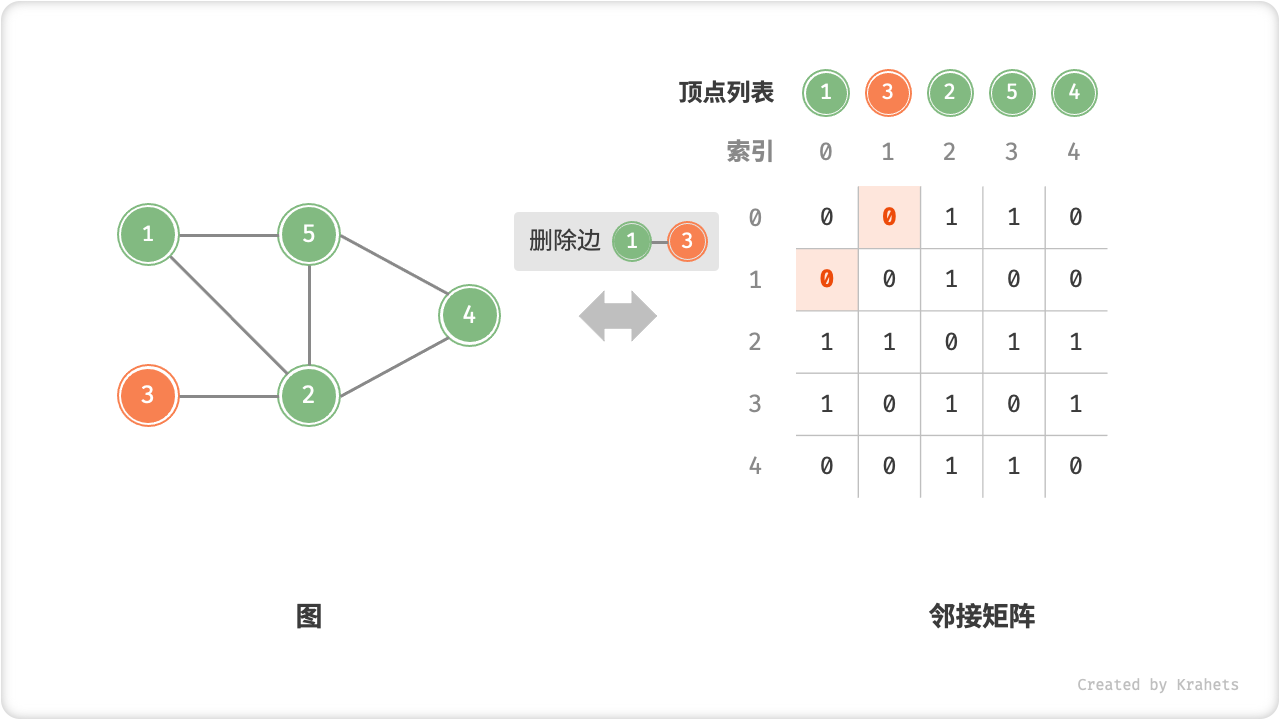
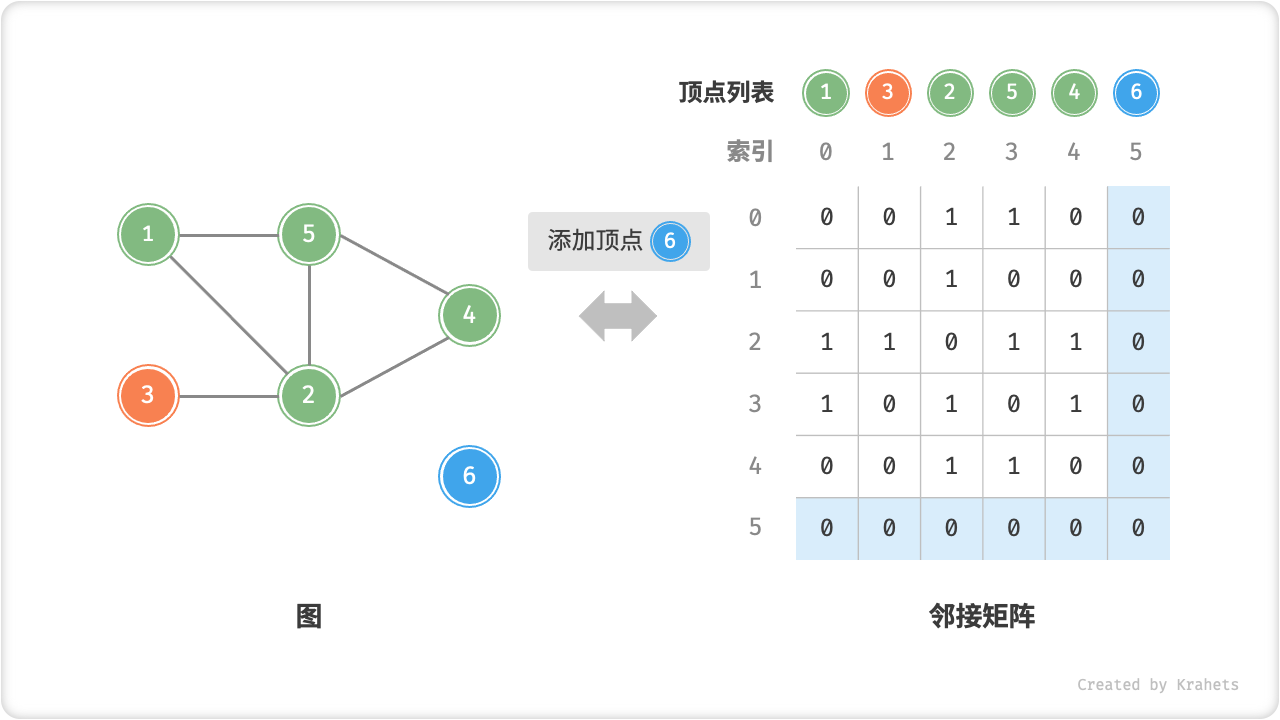
• 添加或删除边：直接在邻接矩阵中修改指定边的对应元素即可，使用 O(1) 时间。而由于是无向图，因此需要同时更新两个方向的边。
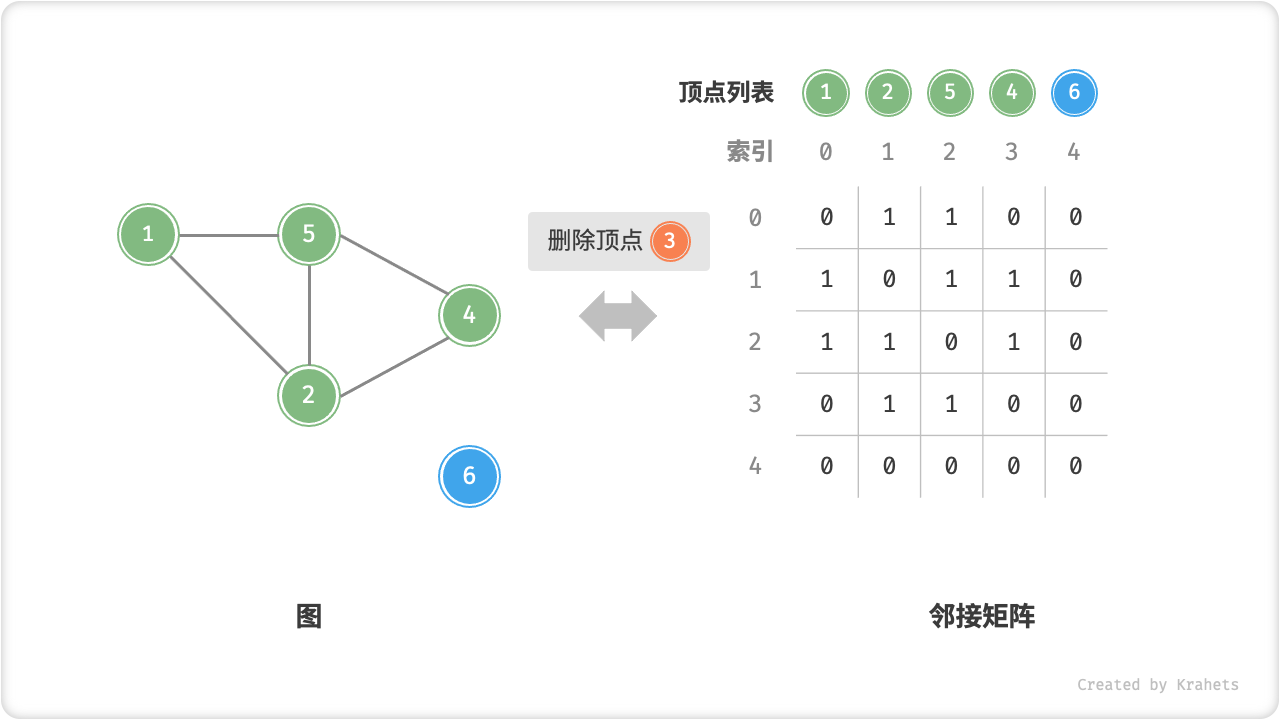
• 添加顶点：在邻接矩阵的尾部添加一行一列，并全部填 0 即可，使用 O(n) 时间。
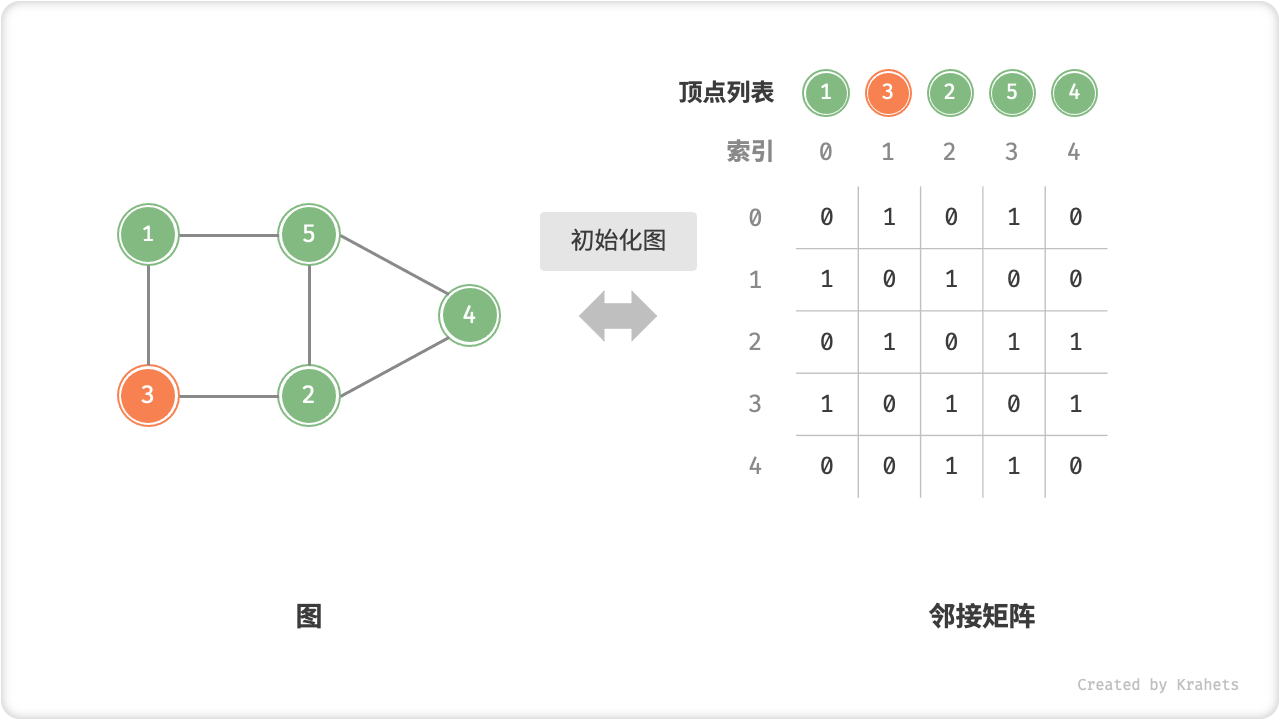
• 删除顶点：在邻接矩阵中删除一行一列。当删除首行首列时达到最差情况，需要将 (n-1)^2 个元素“向左上移动”，从而使用 O(n^2) 时间。
• 初始化：传入 n 个顶点，初始化长度为 n 的顶点列表 vertices ，使用 O(n) 时间；初始化 n \times n 大小的邻接矩阵 adjMat ，使用 O(n^2) 时间。

=== "初始化邻接矩阵"

=== "添加边"

=== "删除边"

=== "添加顶点"

=== "删除顶点"

以下是基于邻接矩阵表示图的实现代码。

=== "Java"

```java title="graph_adjacency_matrix.java"
/* 基于邻接矩阵实现的无向图类 */
class GraphAdjMat {
    List<Integer> vertices;     // 顶点列表，元素代表“顶点值”，索引代表“顶点索引”
    List<List<Integer>> adjMat; // 邻接矩阵，行列索引对应“顶点索引”

    /* 构造函数 */
    public GraphAdjMat(int[] vertices, int[][] edges) {
        this.vertices = new ArrayList<>();
        this.adjMat = new ArrayList<>();
        // 添加顶点
        for (int val : vertices) {
            addVertex(val);
        }
        // 添加边
        // 请注意，edges 元素代表顶点索引，即对应 vertices 元素索引
        for (int[] e : edges) {
            addEdge(e[0], e[1]);
        }
    }

    /* 获取顶点数量 */
    public int size() {
        return vertices.size();
    }

    /* 添加顶点 */
    public void addVertex(int val) {
        int n = size();
        // 向顶点列表中添加新顶点的值
        vertices.add(val);
        // 在邻接矩阵中添加一行
        List<Integer> newRow = new ArrayList<>(n);
        for (int j = 0; j < n; j++) {
            newRow.add(0);
        }
        adjMat.add(newRow);
        // 在邻接矩阵中添加一列
        for (List<Integer> row : adjMat) {
            row.add(0);
        }
    }

    /* 删除顶点 */
    public void removeVertex(int index) {
        if (index >= size())
            throw new IndexOutOfBoundsException();
        // 在顶点列表中移除索引 index 的顶点
        vertices.remove(index);
        // 在邻接矩阵中删除索引 index 的行
        adjMat.remove(index);
        // 在邻接矩阵中删除索引 index 的列
        for (List<Integer> row : adjMat) {
            row.remove(index);
        }
    }

    /* 添加边 */
    // 参数 i, j 对应 vertices 元素索引
    public void addEdge(int i, int j) {
        // 索引越界与相等处理
        if (i < 0 || j < 0 || i >= size() || j >= size() || i == j)
            throw new IndexOutOfBoundsException();
        // 在无向图中，邻接矩阵沿主对角线对称，即满足 (i, j) == (j, i)
        adjMat.get(i).set(j, 1);
        adjMat.get(j).set(i, 1);
    }

    /* 删除边 */
    // 参数 i, j 对应 vertices 元素索引
    public void removeEdge(int i, int j) {
        // 索引越界与相等处理
        if (i < 0 || j < 0 || i >= size() || j >= size() || i == j)
            throw new IndexOutOfBoundsException();
        adjMat.get(i).set(j, 0);
        adjMat.get(j).set(i, 0);
    }
}
```

=== "C++"

```cpp title="graph_adjacency_matrix.cpp"

```

=== "Python"

```python title="graph_adjacency_matrix.py"

```

=== "Go"

```go title="graph_adjacency_matrix.go"

```

=== "JavaScript"

```js title="graph_adjacency_matrix.js"

```

=== "TypeScript"

```typescript title="graph_adjacency_matrix.ts"

```

=== "C"

```c title="graph_adjacency_matrix.c"

```

=== "C#"

```csharp title="graph_adjacency_matrix.cs"

```

=== "Swift"

```swift title="graph_adjacency_matrix.swift"

```

基于邻接表的实现

设图的顶点总数为 n 、边总数为 m ，则有：

• 添加边：在顶点对应链表的尾部添加边即可，使用 O(1) 时间。因为是无向图，所以需要同时添加两个方向的边。
• 删除边：在顶点对应链表中查询与删除指定边，使用 O(m) 时间。与添加边一样，需要同时删除两个方向的边。
• 添加顶点：在邻接表中添加一个链表即可，并以新增顶点为链表头结点，使用 O(1) 时间。
• 删除顶点：需要遍历整个邻接表，删除包含指定顶点的所有边，使用 O(n + m) 时间。
• 初始化：需要在邻接表中建立 n 个结点和 2m 条边，使用 O(n + m) 时间。

=== "初始化邻接表"

=== "添加边"

=== "删除边"

=== "添加顶点"

=== "删除顶点"

基于邻接表实现图的代码如下所示。

=== "Java"

```java title="graph_adjacency_list.java"
/* 顶点类 */
class Vertex {
    int val;
    public Vertex(int val) {
        this.val = val;
    }
}

/* 基于邻接表实现的无向图类 */
class GraphAdjList {
    // 请注意，vertices 和 adjList 中存储的都是 Vertex 对象
    Map<Vertex, Set<Vertex>> adjList; // 邻接表（使用哈希表实现）

    /* 构造函数 */
    public GraphAdjList(Vertex[][] edges) {
        this.adjList = new HashMap<>();
        // 添加所有顶点和边
        for (Vertex[] edge : edges) {
            addVertex(edge[0]);
            addVertex(edge[1]);
            addEdge(edge[0], edge[1]);
        }
    }

    /* 获取顶点数量 */
    public int size() {
        return adjList.size();
    }

    /* 添加边 */
    public void addEdge(Vertex vet1, Vertex vet2) {
        if (!adjList.containsKey(vet1) || !adjList.containsKey(vet2) || vet1 == vet2)
            throw new IllegalArgumentException();
        // 添加边 vet1 - vet2
        adjList.get(vet1).add(vet2);
        adjList.get(vet2).add(vet1);
    }

    /* 删除边 */
    public void removeEdge(Vertex vet1, Vertex vet2) {
        if (!adjList.containsKey(vet1) || !adjList.containsKey(vet2) || vet1 == vet2)
            throw new IllegalArgumentException();
        // 删除边 vet1 - vet2
        adjList.get(vet1).remove(vet2);
        adjList.get(vet2).remove(vet1);
    }

    /* 添加顶点 */
    public void addVertex(Vertex vet) {
        if (adjList.containsKey(vet))
            return;
        // 在邻接表中添加一个新链表（即 HashSet）
        adjList.put(vet, new HashSet<>());
    }

    /* 删除顶点 */
    public void removeVertex(Vertex vet) {
        if (!adjList.containsKey(vet))
            throw new IllegalArgumentException();
        // 在邻接表中删除顶点 vet 对应的链表（即 HashSet）
        adjList.remove(vet);
        // 遍历其它顶点的链表（即 HashSet），删除所有包含 vet 的边
        for (Set<Vertex> set : adjList.values()) {
            set.remove(vet);
        }
    }
}
```

=== "C++"

```cpp title="graph_adjacency_list.cpp"

```

=== "Python"

```python title="graph_adjacency_list.py"

```

=== "Go"

```go title="graph_adjacency_list.go"

```

=== "JavaScript"

```js title="graph_adjacency_list.js"

```

=== "TypeScript"

```typescript title="graph_adjacency_list.ts"

```

=== "C"

```c title="graph_adjacency_list.c"

```

=== "C#"

```csharp title="graph_adjacency_list.cs"

```

=== "Swift"

```swift title="graph_adjacency_list.swift"

```

效率对比

设图中共有 n 个顶点和 m 条边，下表为邻接矩阵和邻接表的时间和空间效率对比。

	邻接矩阵	邻接表（链表）	邻接表（哈希表）
判断是否邻接	O(1)	O(m)	O(1)
添加边	O(1)	O(1)	O(1)
删除边	O(1)	O(m)	O(1)
添加顶点	O(n)	O(1)	O(1)
删除顶点	O(n^2)	O(n + m)	O(n)
内存空间占用	O(n^2)	O(n + m)	O(n + m)

观察上表，貌似邻接表（哈希表）的时间与空间效率最优。但实际上，在邻接矩阵中操作边的效率更高，只需要一次数组访问或赋值操作即可。总结以上，邻接矩阵体现“以空间换时间”，邻接表体现“以时间换空间”。

图常见应用

现实中的许多系统都可以使用图来建模，对应的待求解问题也可以被约化为图计算问题。

	顶点	边	图计算问题
社交网络	用户	好友关系	潜在好友推荐
地铁线路	站点	站点间的连通性	最短路线推荐
太阳系	星体	星体间的万有引力作用	行星轨道计算