* preorder, inorder, postorder -> pre-order, in-order, post-order * Bug fixes * Bug fixes * Update what_is_dsa.md * Sync zh and zh-hant versions * Sync zh and zh-hant versions. * Update performance_evaluation.md and time_complexity.md * Add @khoaxuantu to the landing page. * Sync zh and zh-hant versions * Add @ khoaxuantu to the landing page of zh-hant and en versions.
20 KiB
堆積
堆積(heap)是一種滿足特定條件的完全二元樹,主要可分為兩種型別,如下圖所示。
- 小頂堆積(min heap):任意節點的值
\leq其子節點的值。 - 大頂堆積(max heap):任意節點的值
\geq其子節點的值。
堆積作為完全二元樹的一個特例,具有以下特性。
- 最底層節點靠左填充,其他層的節點都被填滿。
- 我們將二元樹的根節點稱為“堆積頂”,將底層最靠右的節點稱為“堆積底”。
- 對於大頂堆積(小頂堆積),堆積頂元素(根節點)的值是最大(最小)的。
堆積的常用操作
需要指出的是,許多程式語言提供的是優先佇列(priority queue),這是一種抽象的資料結構,定義為具有優先順序排序的佇列。
實際上,堆積通常用於實現優先佇列,大頂堆積相當於元素按從大到小的順序出列的優先佇列。從使用角度來看,我們可以將“優先佇列”和“堆積”看作等價的資料結構。因此,本書對兩者不做特別區分,統一稱作“堆積”。
堆積的常用操作見下表,方法名需要根據程式語言來確定。
表 堆積的操作效率
| 方法名 | 描述 | 時間複雜度 |
|---|---|---|
push() |
元素入堆積 | O(\log n) |
pop() |
堆積頂元素出堆積 | O(\log n) |
peek() |
訪問堆積頂元素(對於大 / 小頂堆積分別為最大 / 小值) | O(1) |
size() |
獲取堆積的元素數量 | O(1) |
isEmpty() |
判斷堆積是否為空 | O(1) |
在實際應用中,我們可以直接使用程式語言提供的堆積類別(或優先佇列類別)。
類似於排序演算法中的“從小到大排列”和“從大到小排列”,我們可以透過設定一個 flag 或修改 Comparator 實現“小頂堆積”與“大頂堆積”之間的轉換。程式碼如下所示:
=== "Python"
```python title="heap.py"
# 初始化小頂堆積
min_heap, flag = [], 1
# 初始化大頂堆積
max_heap, flag = [], -1
# Python 的 heapq 模組預設實現小頂堆積
# 考慮將“元素取負”後再入堆積,這樣就可以將大小關係顛倒,從而實現大頂堆積
# 在本示例中,flag = 1 時對應小頂堆積,flag = -1 時對應大頂堆積
# 元素入堆積
heapq.heappush(max_heap, flag * 1)
heapq.heappush(max_heap, flag * 3)
heapq.heappush(max_heap, flag * 2)
heapq.heappush(max_heap, flag * 5)
heapq.heappush(max_heap, flag * 4)
# 獲取堆積頂元素
peek: int = flag * max_heap[0] # 5
# 堆積頂元素出堆積
# 出堆積元素會形成一個從大到小的序列
val = flag * heapq.heappop(max_heap) # 5
val = flag * heapq.heappop(max_heap) # 4
val = flag * heapq.heappop(max_heap) # 3
val = flag * heapq.heappop(max_heap) # 2
val = flag * heapq.heappop(max_heap) # 1
# 獲取堆積大小
size: int = len(max_heap)
# 判斷堆積是否為空
is_empty: bool = not max_heap
# 輸入串列並建堆積
min_heap: list[int] = [1, 3, 2, 5, 4]
heapq.heapify(min_heap)
```
=== "C++"
```cpp title="heap.cpp"
/* 初始化堆積 */
// 初始化小頂堆積
priority_queue<int, vector<int>, greater<int>> minHeap;
// 初始化大頂堆積
priority_queue<int, vector<int>, less<int>> maxHeap;
/* 元素入堆積 */
maxHeap.push(1);
maxHeap.push(3);
maxHeap.push(2);
maxHeap.push(5);
maxHeap.push(4);
/* 獲取堆積頂元素 */
int peek = maxHeap.top(); // 5
/* 堆積頂元素出堆積 */
// 出堆積元素會形成一個從大到小的序列
maxHeap.pop(); // 5
maxHeap.pop(); // 4
maxHeap.pop(); // 3
maxHeap.pop(); // 2
maxHeap.pop(); // 1
/* 獲取堆積大小 */
int size = maxHeap.size();
/* 判斷堆積是否為空 */
bool isEmpty = maxHeap.empty();
/* 輸入串列並建堆積 */
vector<int> input{1, 3, 2, 5, 4};
priority_queue<int, vector<int>, greater<int>> minHeap(input.begin(), input.end());
```
=== "Java"
```java title="heap.java"
/* 初始化堆積 */
// 初始化小頂堆積
Queue<Integer> minHeap = new PriorityQueue<>();
// 初始化大頂堆積(使用 lambda 表示式修改 Comparator 即可)
Queue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b - a);
/* 元素入堆積 */
maxHeap.offer(1);
maxHeap.offer(3);
maxHeap.offer(2);
maxHeap.offer(5);
maxHeap.offer(4);
/* 獲取堆積頂元素 */
int peek = maxHeap.peek(); // 5
/* 堆積頂元素出堆積 */
// 出堆積元素會形成一個從大到小的序列
peek = maxHeap.poll(); // 5
peek = maxHeap.poll(); // 4
peek = maxHeap.poll(); // 3
peek = maxHeap.poll(); // 2
peek = maxHeap.poll(); // 1
/* 獲取堆積大小 */
int size = maxHeap.size();
/* 判斷堆積是否為空 */
boolean isEmpty = maxHeap.isEmpty();
/* 輸入串列並建堆積 */
minHeap = new PriorityQueue<>(Arrays.asList(1, 3, 2, 5, 4));
```
=== "C#"
```csharp title="heap.cs"
/* 初始化堆積 */
// 初始化小頂堆積
PriorityQueue<int, int> minHeap = new();
// 初始化大頂堆積(使用 lambda 表示式修改 Comparator 即可)
PriorityQueue<int, int> maxHeap = new(Comparer<int>.Create((x, y) => y - x));
/* 元素入堆積 */
maxHeap.Enqueue(1, 1);
maxHeap.Enqueue(3, 3);
maxHeap.Enqueue(2, 2);
maxHeap.Enqueue(5, 5);
maxHeap.Enqueue(4, 4);
/* 獲取堆積頂元素 */
int peek = maxHeap.Peek();//5
/* 堆積頂元素出堆積 */
// 出堆積元素會形成一個從大到小的序列
peek = maxHeap.Dequeue(); // 5
peek = maxHeap.Dequeue(); // 4
peek = maxHeap.Dequeue(); // 3
peek = maxHeap.Dequeue(); // 2
peek = maxHeap.Dequeue(); // 1
/* 獲取堆積大小 */
int size = maxHeap.Count;
/* 判斷堆積是否為空 */
bool isEmpty = maxHeap.Count == 0;
/* 輸入串列並建堆積 */
minHeap = new PriorityQueue<int, int>([(1, 1), (3, 3), (2, 2), (5, 5), (4, 4)]);
```
=== "Go"
```go title="heap.go"
// Go 語言中可以透過實現 heap.Interface 來構建整數大頂堆積
// 實現 heap.Interface 需要同時實現 sort.Interface
type intHeap []any
// Push heap.Interface 的方法,實現推入元素到堆積
func (h *intHeap) Push(x any) {
// Push 和 Pop 使用 pointer receiver 作為參數
// 因為它們不僅會對切片的內容進行調整,還會修改切片的長度。
*h = append(*h, x.(int))
}
// Pop heap.Interface 的方法,實現彈出堆積頂元素
func (h *intHeap) Pop() any {
// 待出堆積元素存放在最後
last := (*h)[len(*h)-1]
*h = (*h)[:len(*h)-1]
return last
}
// Len sort.Interface 的方法
func (h *intHeap) Len() int {
return len(*h)
}
// Less sort.Interface 的方法
func (h *intHeap) Less(i, j int) bool {
// 如果實現小頂堆積,則需要調整為小於號
return (*h)[i].(int) > (*h)[j].(int)
}
// Swap sort.Interface 的方法
func (h *intHeap) Swap(i, j int) {
(*h)[i], (*h)[j] = (*h)[j], (*h)[i]
}
// Top 獲取堆積頂元素
func (h *intHeap) Top() any {
return (*h)[0]
}
/* Driver Code */
func TestHeap(t *testing.T) {
/* 初始化堆積 */
// 初始化大頂堆積
maxHeap := &intHeap{}
heap.Init(maxHeap)
/* 元素入堆積 */
// 呼叫 heap.Interface 的方法,來新增元素
heap.Push(maxHeap, 1)
heap.Push(maxHeap, 3)
heap.Push(maxHeap, 2)
heap.Push(maxHeap, 4)
heap.Push(maxHeap, 5)
/* 獲取堆積頂元素 */
top := maxHeap.Top()
fmt.Printf("堆積頂元素為 %d\n", top)
/* 堆積頂元素出堆積 */
// 呼叫 heap.Interface 的方法,來移除元素
heap.Pop(maxHeap) // 5
heap.Pop(maxHeap) // 4
heap.Pop(maxHeap) // 3
heap.Pop(maxHeap) // 2
heap.Pop(maxHeap) // 1
/* 獲取堆積大小 */
size := len(*maxHeap)
fmt.Printf("堆積元素數量為 %d\n", size)
/* 判斷堆積是否為空 */
isEmpty := len(*maxHeap) == 0
fmt.Printf("堆積是否為空 %t\n", isEmpty)
}
```
=== "Swift"
```swift title="heap.swift"
/* 初始化堆積 */
// Swift 的 Heap 型別同時支持最大堆積和最小堆積,且需要引入 swift-collections
var heap = Heap<Int>()
/* 元素入堆積 */
heap.insert(1)
heap.insert(3)
heap.insert(2)
heap.insert(5)
heap.insert(4)
/* 獲取堆積頂元素 */
var peek = heap.max()!
/* 堆積頂元素出堆積 */
peek = heap.removeMax() // 5
peek = heap.removeMax() // 4
peek = heap.removeMax() // 3
peek = heap.removeMax() // 2
peek = heap.removeMax() // 1
/* 獲取堆積大小 */
let size = heap.count
/* 判斷堆積是否為空 */
let isEmpty = heap.isEmpty
/* 輸入串列並建堆積 */
let heap2 = Heap([1, 3, 2, 5, 4])
```
=== "JS"
```javascript title="heap.js"
// JavaScript 未提供內建 Heap 類別
```
=== "TS"
```typescript title="heap.ts"
// TypeScript 未提供內建 Heap 類別
```
=== "Dart"
```dart title="heap.dart"
// Dart 未提供內建 Heap 類別
```
=== "Rust"
```rust title="heap.rs"
use std::collections::BinaryHeap;
use std::cmp::Reverse;
/* 初始化堆積 */
// 初始化小頂堆積
let mut min_heap = BinaryHeap::<Reverse<i32>>::new();
// 初始化大頂堆積
let mut max_heap = BinaryHeap::new();
/* 元素入堆積 */
max_heap.push(1);
max_heap.push(3);
max_heap.push(2);
max_heap.push(5);
max_heap.push(4);
/* 獲取堆積頂元素 */
let peek = max_heap.peek().unwrap(); // 5
/* 堆積頂元素出堆積 */
// 出堆積元素會形成一個從大到小的序列
let peek = max_heap.pop().unwrap(); // 5
let peek = max_heap.pop().unwrap(); // 4
let peek = max_heap.pop().unwrap(); // 3
let peek = max_heap.pop().unwrap(); // 2
let peek = max_heap.pop().unwrap(); // 1
/* 獲取堆積大小 */
let size = max_heap.len();
/* 判斷堆積是否為空 */
let is_empty = max_heap.is_empty();
/* 輸入串列並建堆積 */
let min_heap = BinaryHeap::from(vec![Reverse(1), Reverse(3), Reverse(2), Reverse(5), Reverse(4)]);
```
=== "C"
```c title="heap.c"
// C 未提供內建 Heap 類別
```
=== "Kotlin"
```kotlin title="heap.kt"
/* 初始化堆積 */
// 初始化小頂堆積
var minHeap = PriorityQueue<Int>()
// 初始化大頂堆積(使用 lambda 表示式修改 Comparator 即可)
val maxHeap = PriorityQueue { a: Int, b: Int -> b - a }
/* 元素入堆積 */
maxHeap.offer(1)
maxHeap.offer(3)
maxHeap.offer(2)
maxHeap.offer(5)
maxHeap.offer(4)
/* 獲取堆積頂元素 */
var peek = maxHeap.peek() // 5
/* 堆積頂元素出堆積 */
// 出堆積元素會形成一個從大到小的序列
peek = maxHeap.poll() // 5
peek = maxHeap.poll() // 4
peek = maxHeap.poll() // 3
peek = maxHeap.poll() // 2
peek = maxHeap.poll() // 1
/* 獲取堆積大小 */
val size = maxHeap.size
/* 判斷堆積是否為空 */
val isEmpty = maxHeap.isEmpty()
/* 輸入串列並建堆積 */
minHeap = PriorityQueue(mutableListOf(1, 3, 2, 5, 4))
```
=== "Ruby"
```ruby title="heap.rb"
# Ruby 未提供內建 Heap 類別
```
=== "Zig"
```zig title="heap.zig"
```
??? pythontutor "視覺化執行"
https://pythontutor.com/render.html#code=import%20heapq%0A%0A%22%22%22Driver%20Code%22%22%22%0Aif%20__name__%20%3D%3D%20%22__main__%22%3A%0A%20%20%20%20%23%20%E5%88%9D%E5%A7%8B%E5%8C%96%E5%B0%8F%E9%A0%82%E5%A0%86%E7%A9%8D%0A%20%20%20%20min_heap%2C%20flag%20%3D%20%5B%5D%2C%201%0A%20%20%20%20%23%20%E5%88%9D%E5%A7%8B%E5%8C%96%E5%A4%A7%E9%A0%82%E5%A0%86%E7%A9%8D%0A%20%20%20%20max_heap%2C%20flag%20%3D%20%5B%5D%2C%20-1%0A%20%20%20%20%0A%20%20%20%20%23%20Python%20%E7%9A%84%20heapq%20%E6%A8%A1%E7%B5%84%E9%A0%90%E8%A8%AD%E5%AF%A6%E7%8F%BE%E5%B0%8F%E9%A0%82%E5%A0%86%E7%A9%8D%0A%20%20%20%20%23%20%E8%80%83%E6%85%AE%E5%B0%87%E2%80%9C%E5%85%83%E7%B4%A0%E5%8F%96%E8%B2%A0%E2%80%9D%E5%BE%8C%E5%86%8D%E5%85%A5%E5%A0%86%E7%A9%8D%EF%BC%8C%E9%80%99%E6%A8%A3%E5%B0%B1%E5%8F%AF%E4%BB%A5%E5%B0%87%E5%A4%A7%E5%B0%8F%E9%97%9C%E4%BF%82%E9%A1%9B%E5%80%92%EF%BC%8C%E5%BE%9E%E8%80%8C%E5%AF%A6%E7%8F%BE%E5%A4%A7%E9%A0%82%E5%A0%86%E7%A9%8D%0A%20%20%20%20%23%20%E5%9C%A8%E6%9C%AC%E7%A4%BA%E4%BE%8B%E4%B8%AD%EF%BC%8Cflag%20%3D%201%20%E6%99%82%E5%B0%8D%E6%87%89%E5%B0%8F%E9%A0%82%E5%A0%86%E7%A9%8D%EF%BC%8Cflag%20%3D%20-1%20%E6%99%82%E5%B0%8D%E6%87%89%E5%A4%A7%E9%A0%82%E5%A0%86%E7%A9%8D%0A%20%20%20%20%0A%20%20%20%20%23%20%E5%85%83%E7%B4%A0%E5%85%A5%E5%A0%86%E7%A9%8D%0A%20%20%20%20heapq.heappush%28max_heap%2C%20flag%20%2A%201%29%0A%20%20%20%20heapq.heappush%28max_heap%2C%20flag%20%2A%203%29%0A%20%20%20%20heapq.heappush%28max_heap%2C%20flag%20%2A%202%29%0A%20%20%20%20heapq.heappush%28max_heap%2C%20flag%20%2A%205%29%0A%20%20%20%20heapq.heappush%28max_heap%2C%20flag%20%2A%204%29%0A%20%20%20%20%0A%20%20%20%20%23%20%E7%8D%B2%E5%8F%96%E5%A0%86%E7%A9%8D%E9%A0%82%E5%85%83%E7%B4%A0%0A%20%20%20%20peek%20%3D%20flag%20%2A%20max_heap%5B0%5D%20%23%205%0A%20%20%20%20%0A%20%20%20%20%23%20%E5%A0%86%E7%A9%8D%E9%A0%82%E5%85%83%E7%B4%A0%E5%87%BA%E5%A0%86%E7%A9%8D%0A%20%20%20%20%23%20%E5%87%BA%E5%A0%86%E7%A9%8D%E5%85%83%E7%B4%A0%E6%9C%83%E5%BD%A2%E6%88%90%E4%B8%80%E5%80%8B%E5%BE%9E%E5%A4%A7%E5%88%B0%E5%B0%8F%E7%9A%84%E5%BA%8F%E5%88%97%0A%20%20%20%20val%20%3D%20flag%20%2A%20heapq.heappop%28max_heap%29%20%23%205%0A%20%20%20%20val%20%3D%20flag%20%2A%20heapq.heappop%28max_heap%29%20%23%204%0A%20%20%20%20val%20%3D%20flag%20%2A%20heapq.heappop%28max_heap%29%20%23%203%0A%20%20%20%20val%20%3D%20flag%20%2A%20heapq.heappop%28max_heap%29%20%23%202%0A%20%20%20%20val%20%3D%20flag%20%2A%20heapq.heappop%28max_heap%29%20%23%201%0A%20%20%20%20%0A%20%20%20%20%23%20%E7%8D%B2%E5%8F%96%E5%A0%86%E7%A9%8D%E5%A4%A7%E5%B0%8F%0A%20%20%20%20size%20%3D%20len%28max_heap%29%0A%20%20%20%20%0A%20%20%20%20%23%20%E5%88%A4%E6%96%B7%E5%A0%86%E7%A9%8D%E6%98%AF%E5%90%A6%E7%82%BA%E7%A9%BA%0A%20%20%20%20is_empty%20%3D%20not%20max_heap%0A%20%20%20%20%0A%20%20%20%20%23%20%E8%BC%B8%E5%85%A5%E4%B8%B2%E5%88%97%E4%B8%A6%E5%BB%BA%E5%A0%86%E7%A9%8D%0A%20%20%20%20min_heap%20%3D%20%5B1%2C%203%2C%202%2C%205%2C%204%5D%0A%20%20%20%20heapq.heapify%28min_heap%29&cumulative=false&curInstr=3&heapPrimitives=nevernest&mode=display&origin=opt-frontend.js&py=311&rawInputLstJSON=%5B%5D&textReferences=false
堆積的實現
下文實現的是大頂堆積。若要將其轉換為小頂堆積,只需將所有大小邏輯判斷進行逆轉(例如,將 \geq 替換為 \leq )。感興趣的讀者可以自行實現。
堆積的儲存與表示
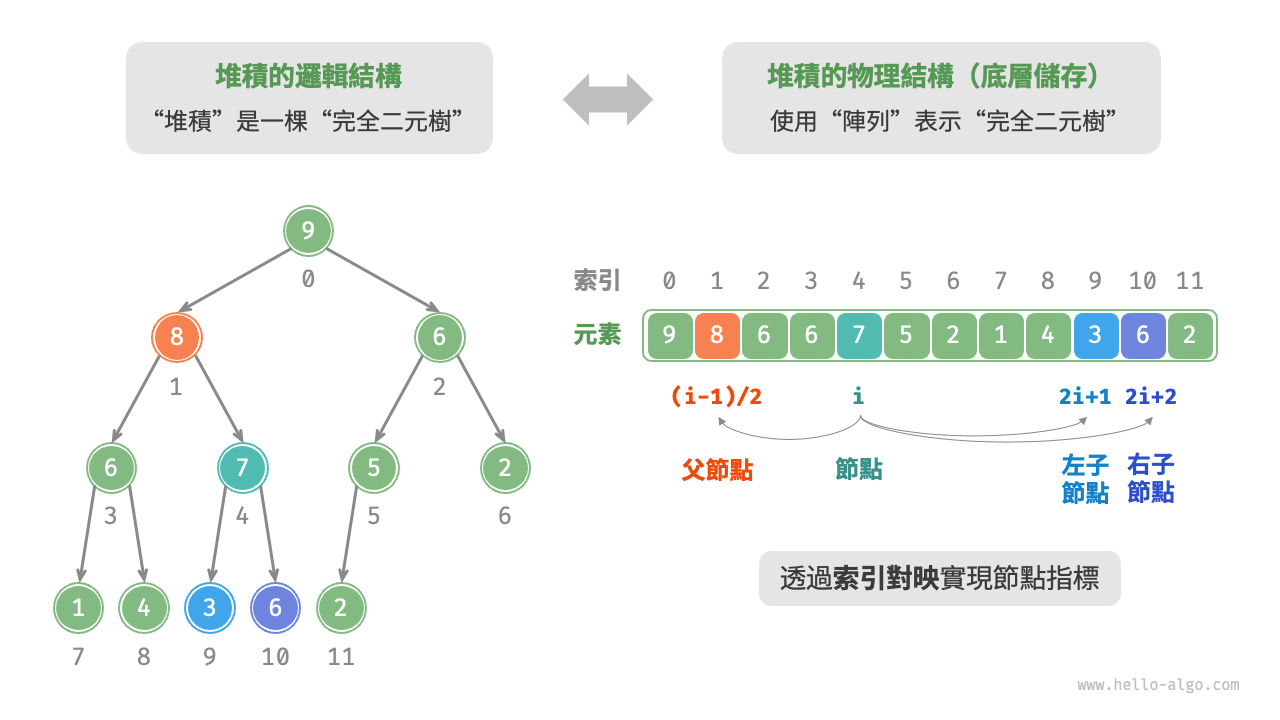
“二元樹”章節講過,完全二元樹非常適合用陣列來表示。由於堆積正是一種完全二元樹,因此我們將採用陣列來儲存堆積。
當使用陣列表示二元樹時,元素代表節點值,索引代表節點在二元樹中的位置。節點指標透過索引對映公式來實現。
如下圖所示,給定索引 i ,其左子節點的索引為 2i + 1 ,右子節點的索引為 2i + 2 ,父節點的索引為 $(i - 1) / 2$(向下整除)。當索引越界時,表示空節點或節點不存在。
我們可以將索引對映公式封裝成函式,方便後續使用:
[file]{my_heap}-[class]{max_heap}-[func]{parent}
訪問堆積頂元素
堆積頂元素即為二元樹的根節點,也就是串列的首個元素:
[file]{my_heap}-[class]{max_heap}-[func]{peek}
元素入堆積
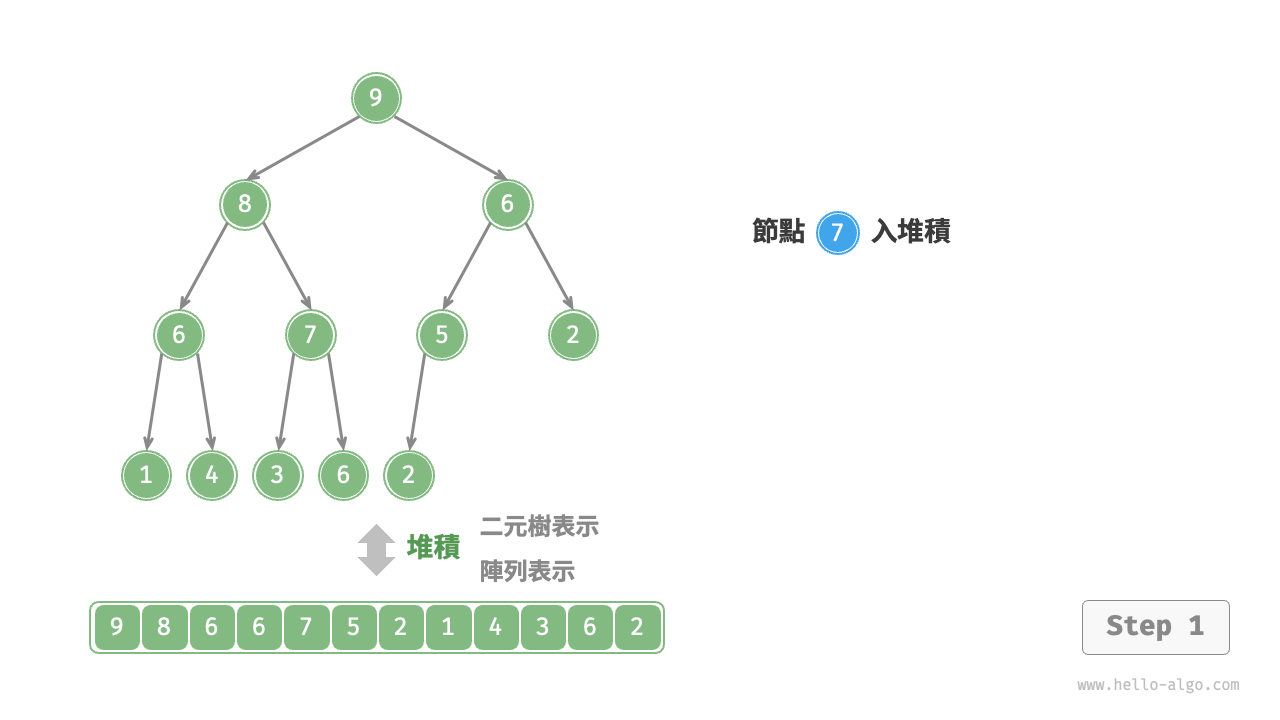
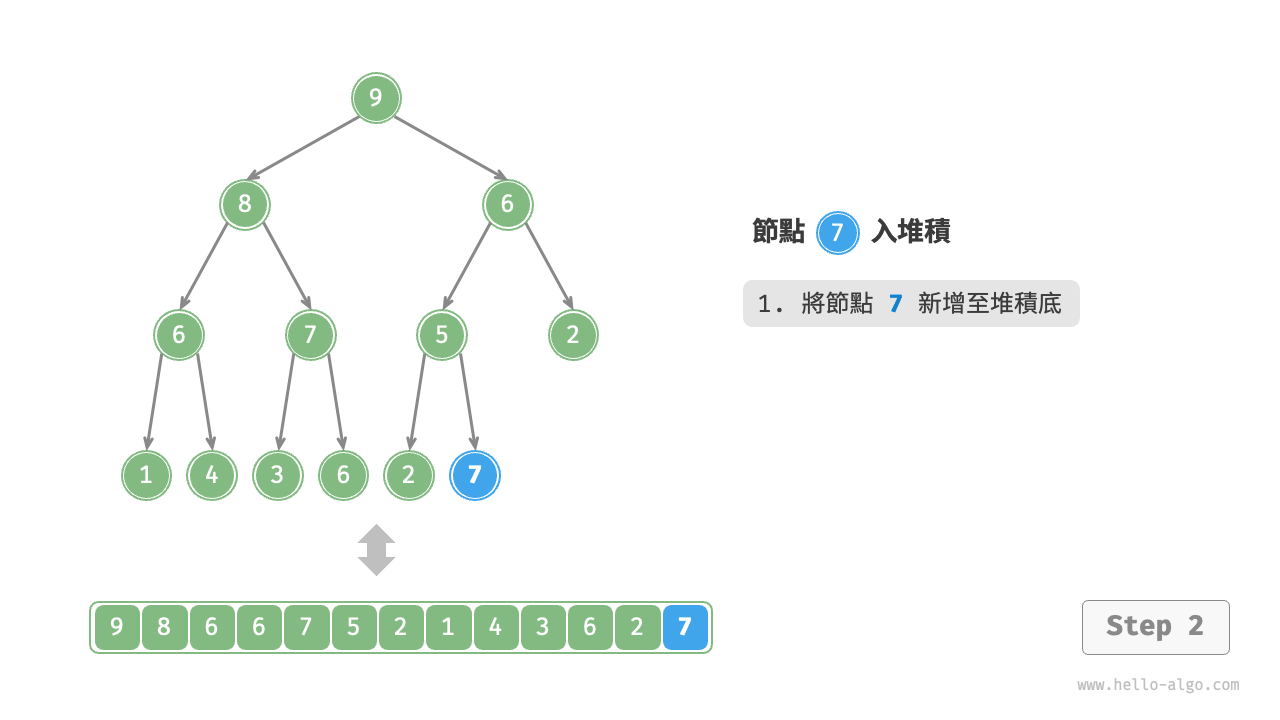
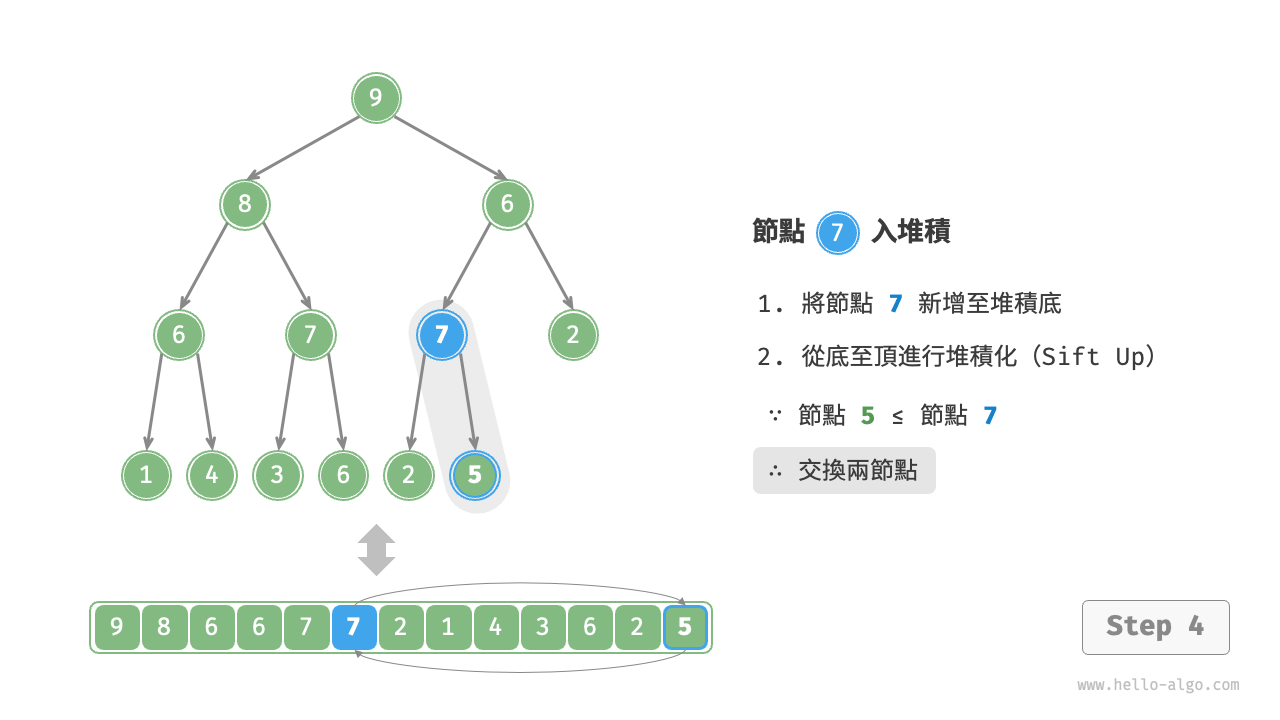
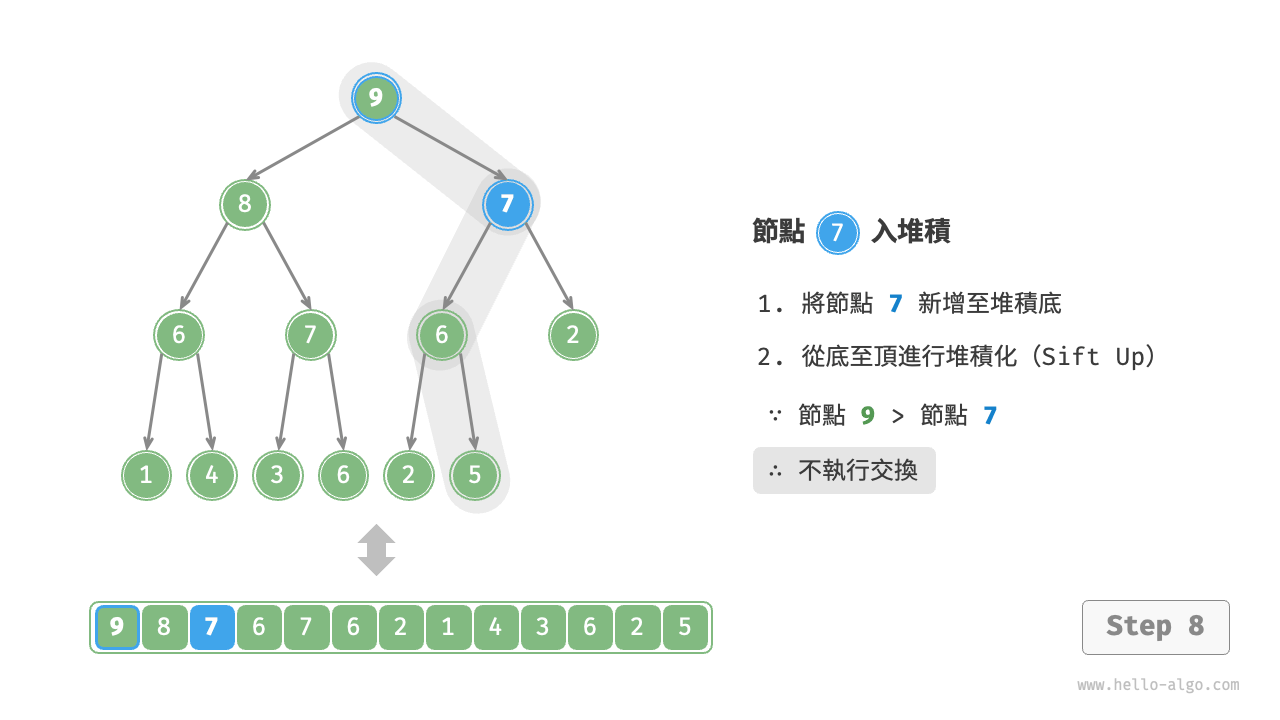
給定元素 val ,我們首先將其新增到堆積底。新增之後,由於 val 可能大於堆積中其他元素,堆積的成立條件可能已被破壞,因此需要修復從插入節點到根節點的路徑上的各個節點,這個操作被稱為堆積化(heapify)。
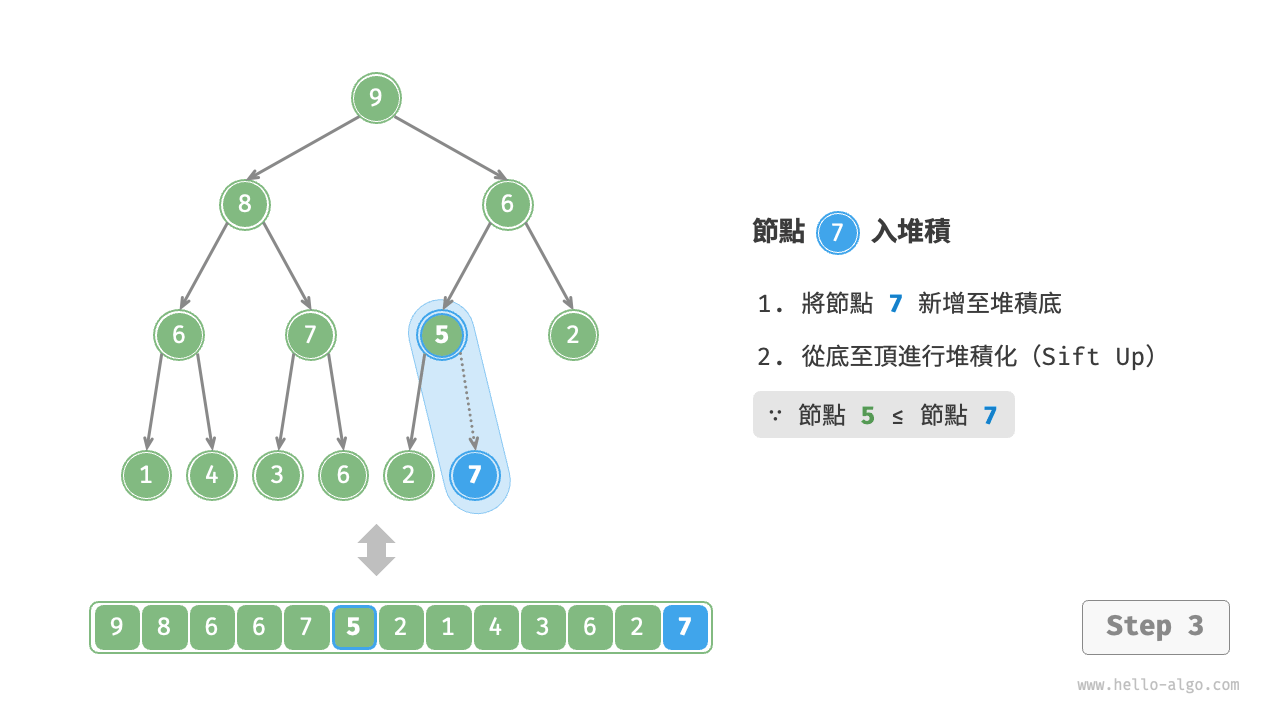
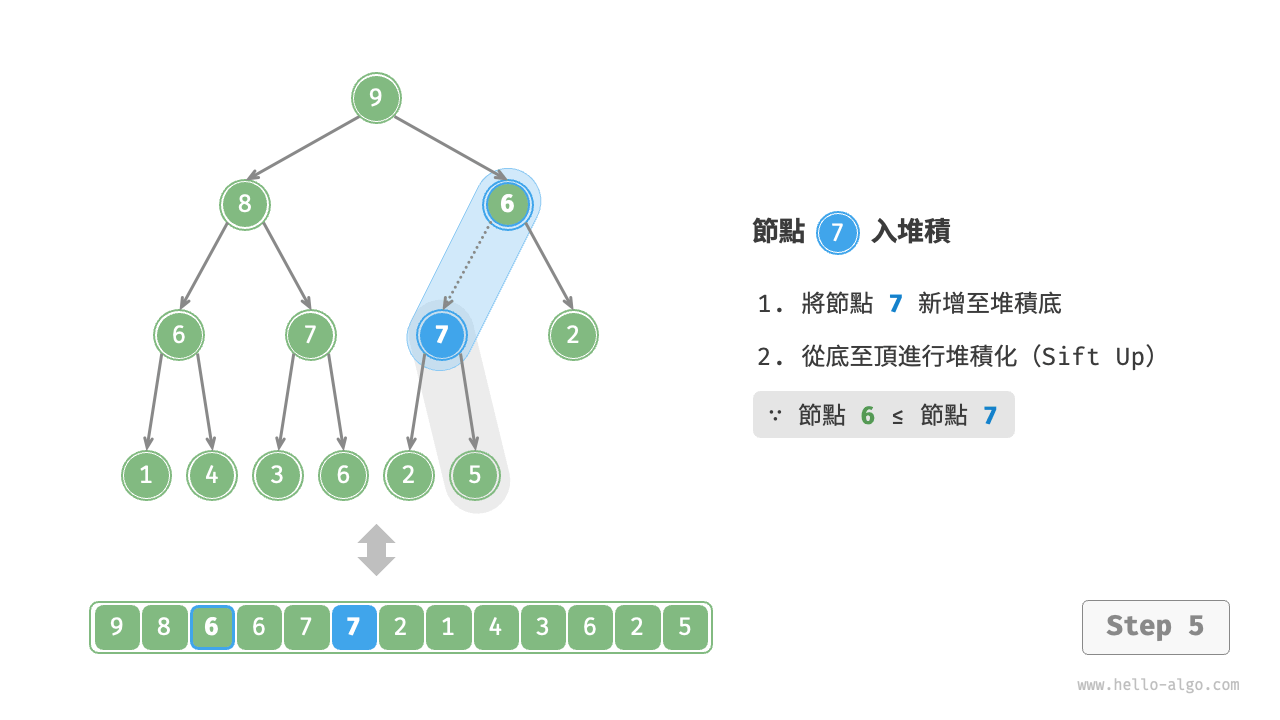
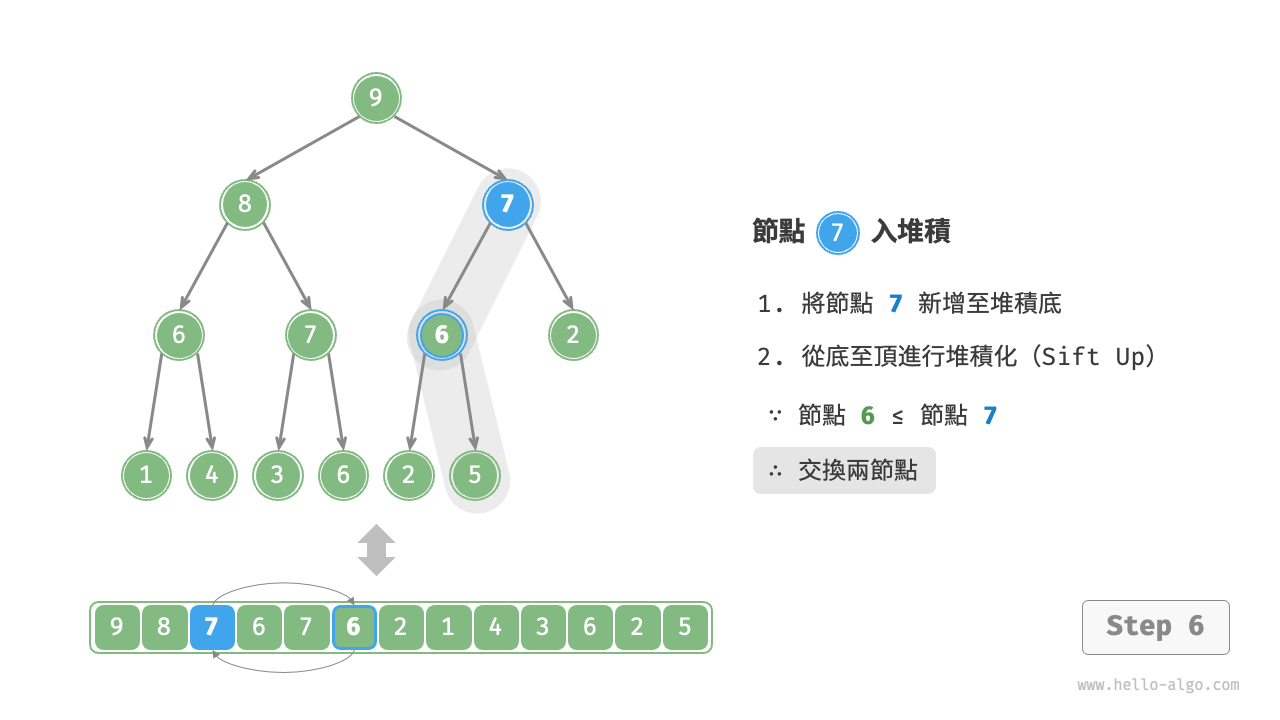
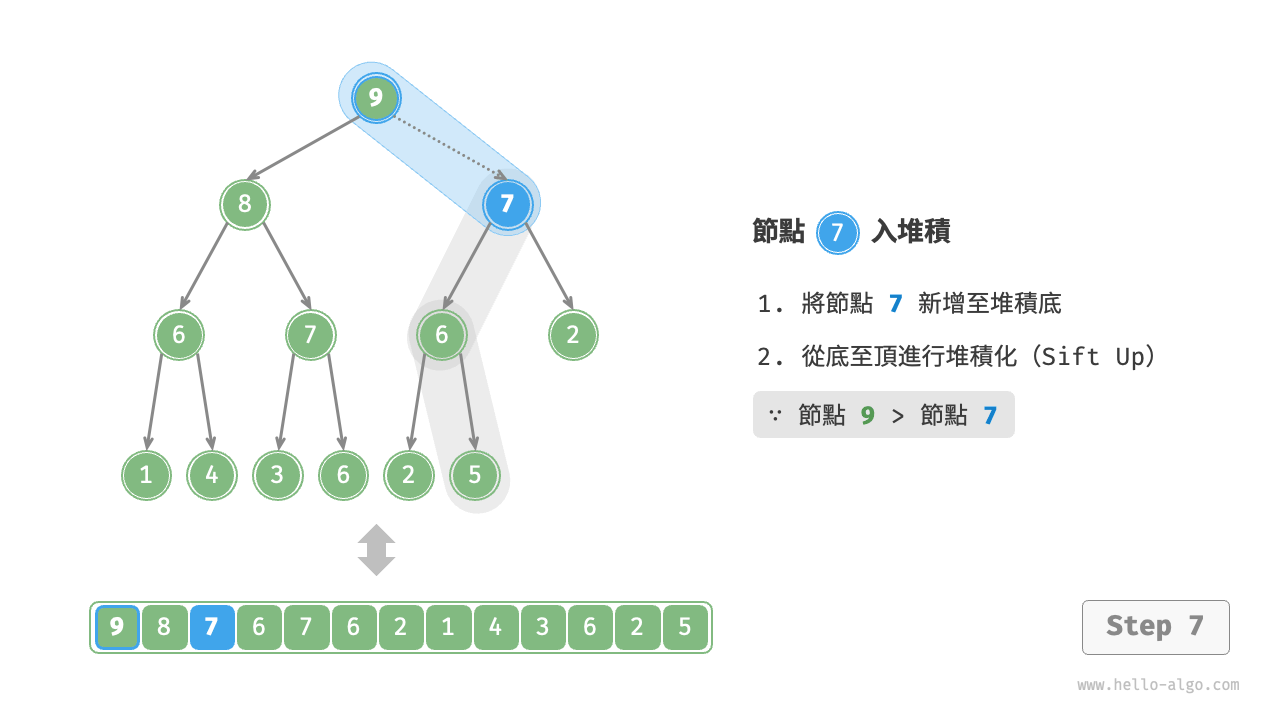
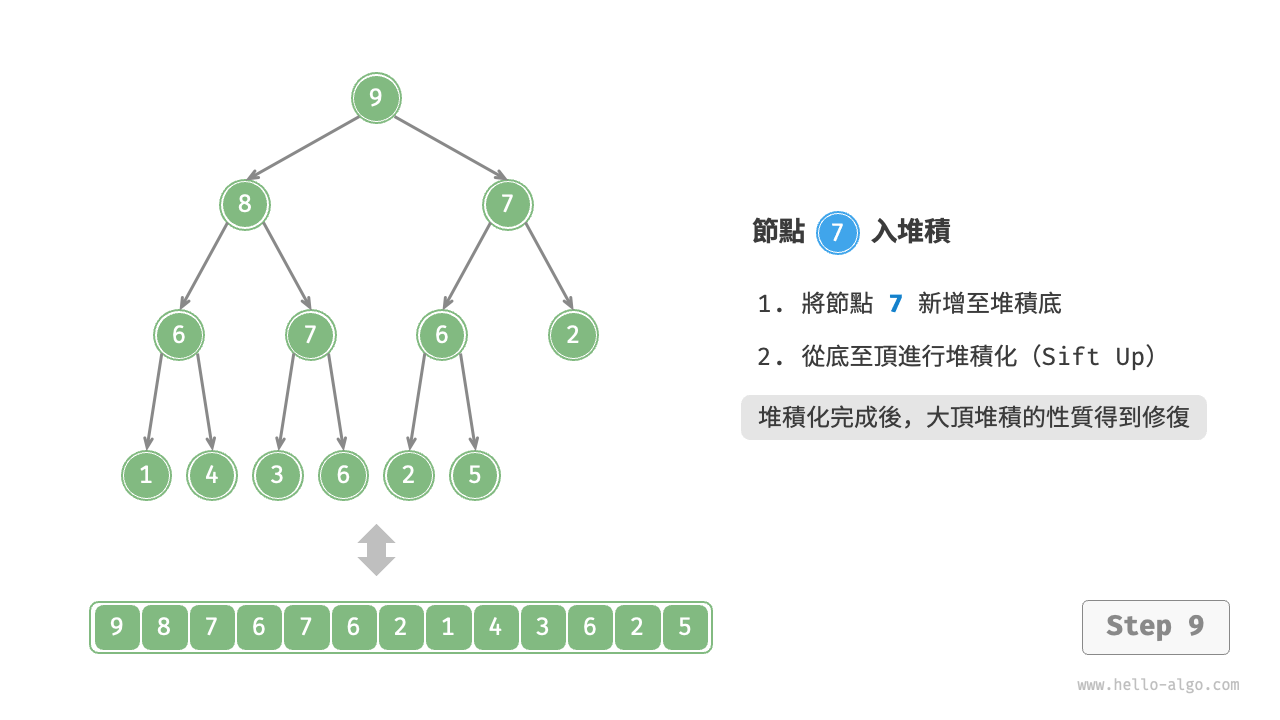
考慮從入堆積節點開始,從底至頂執行堆積化。如下圖所示,我們比較插入節點與其父節點的值,如果插入節點更大,則將它們交換。然後繼續執行此操作,從底至頂修復堆積中的各個節點,直至越過根節點或遇到無須交換的節點時結束。
設節點總數為 n ,則樹的高度為 O(\log n) 。由此可知,堆積化操作的迴圈輪數最多為 O(\log n) ,元素入堆積操作的時間複雜度為 $O(\log n)$ 。程式碼如下所示:
[file]{my_heap}-[class]{max_heap}-[func]{sift_up}
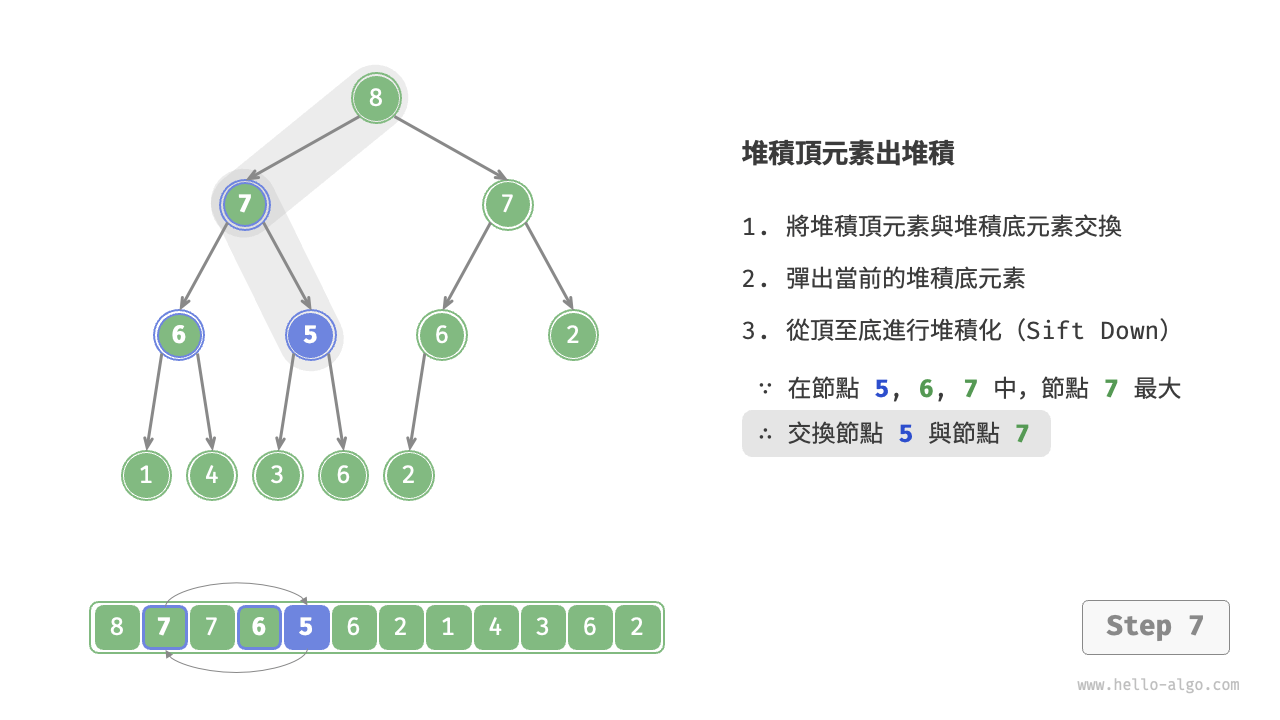
堆積頂元素出堆積
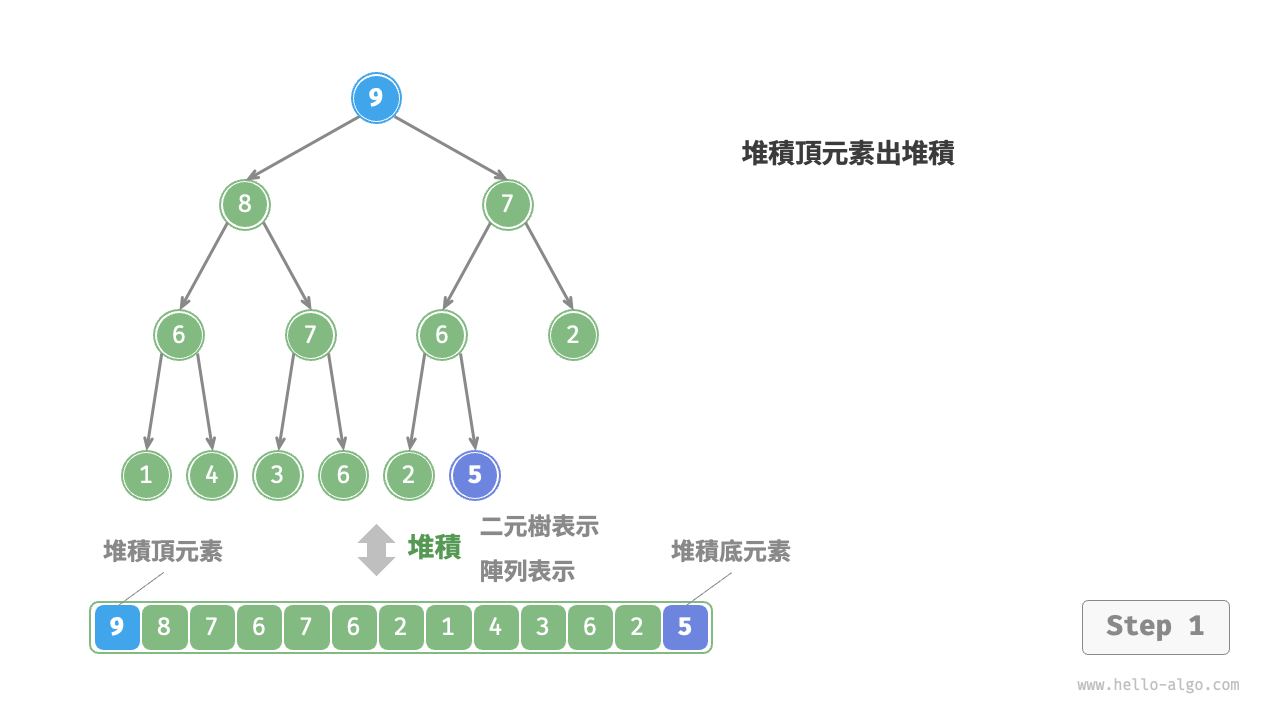
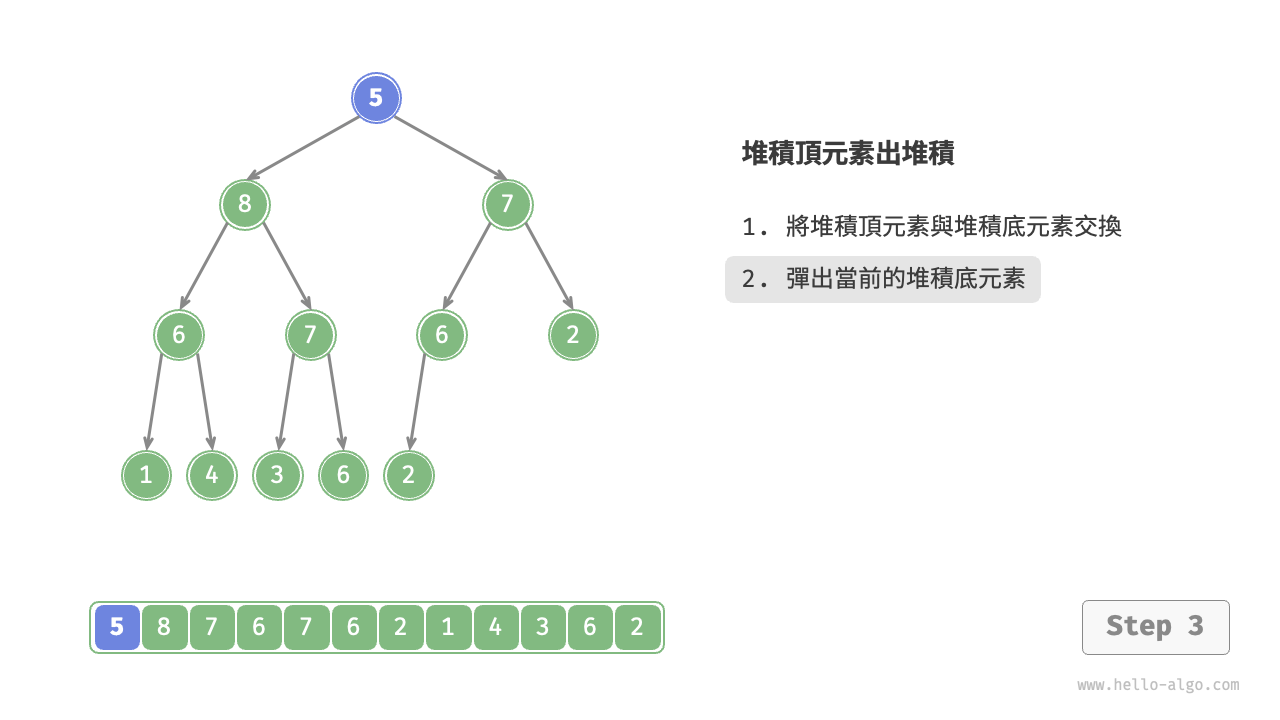
堆積頂元素是二元樹的根節點,即串列首元素。如果我們直接從串列中刪除首元素,那麼二元樹中所有節點的索引都會發生變化,這將使得後續使用堆積化進行修復變得困難。為了儘量減少元素索引的變動,我們採用以下操作步驟。
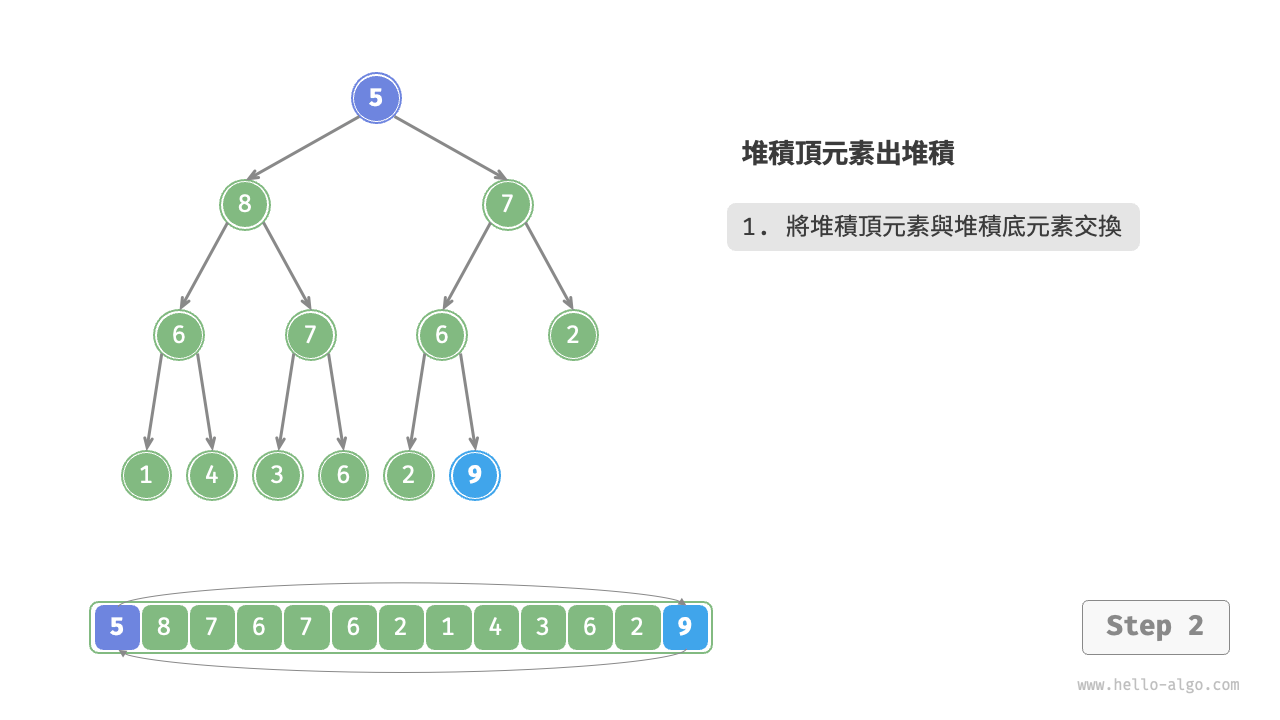
- 交換堆積頂元素與堆積底元素(交換根節點與最右葉節點)。
- 交換完成後,將堆積底從串列中刪除(注意,由於已經交換,因此實際上刪除的是原來的堆積頂元素)。
- 從根節點開始,從頂至底執行堆積化。
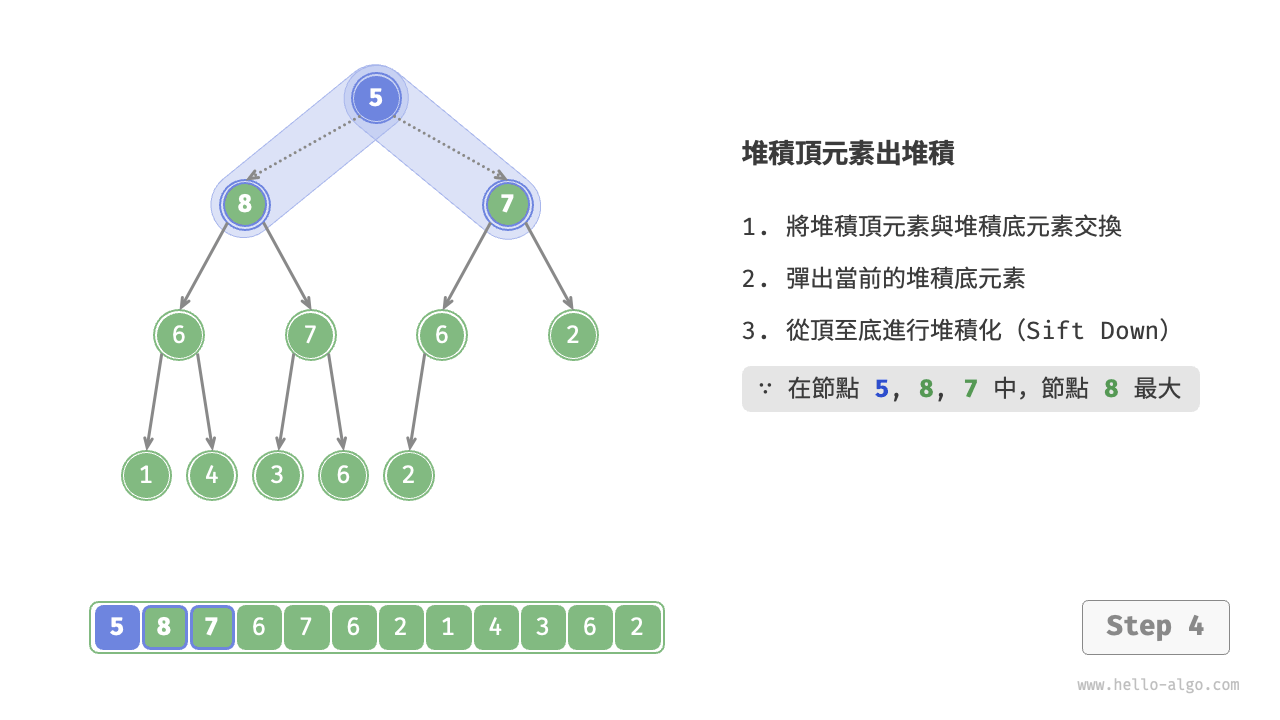
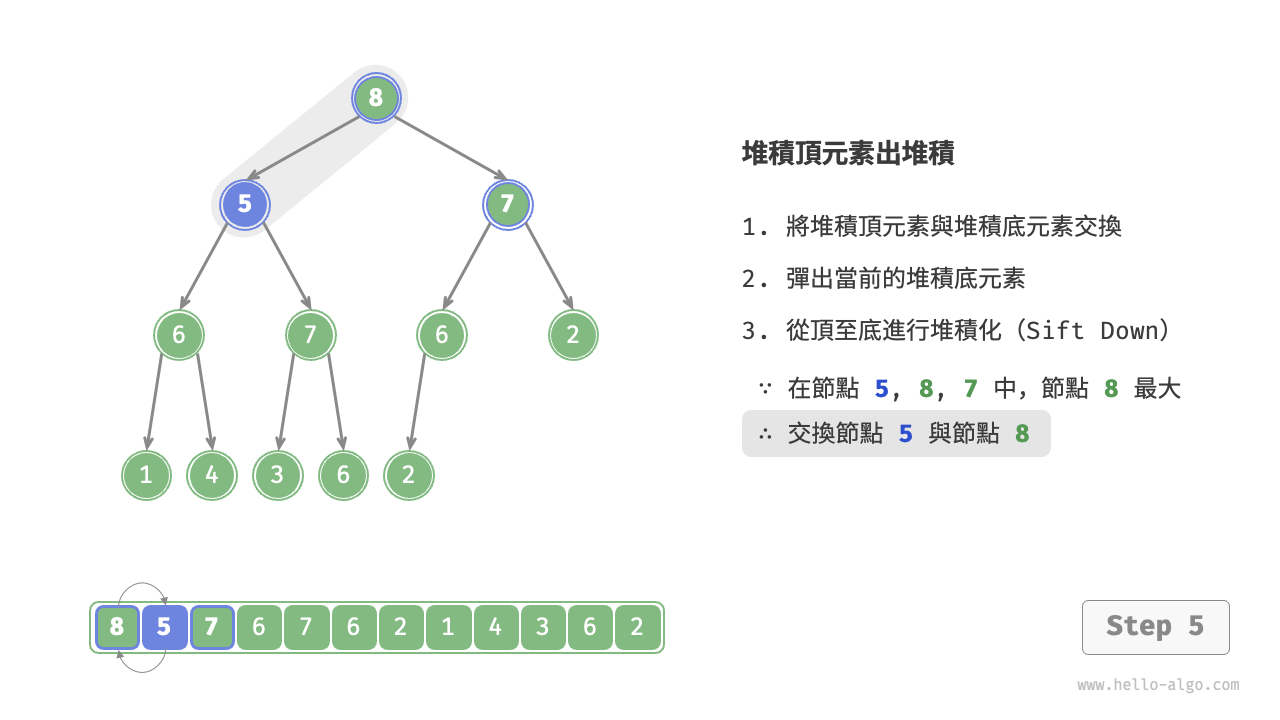
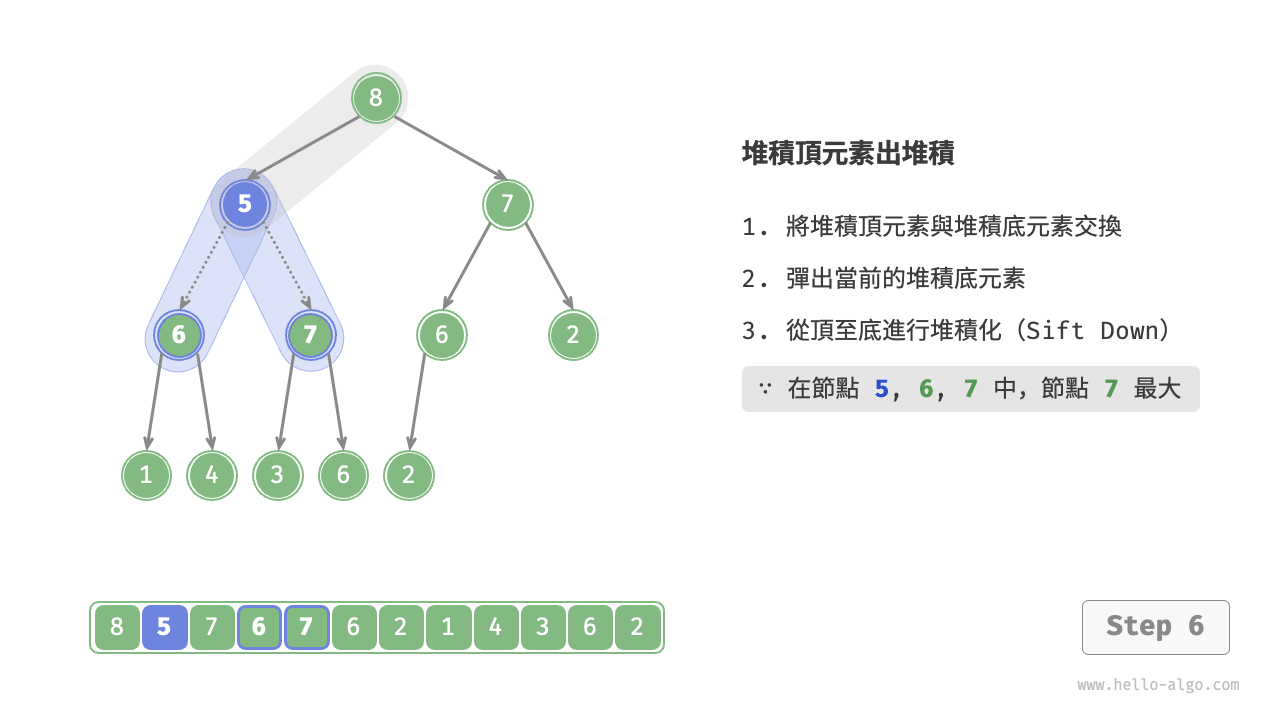
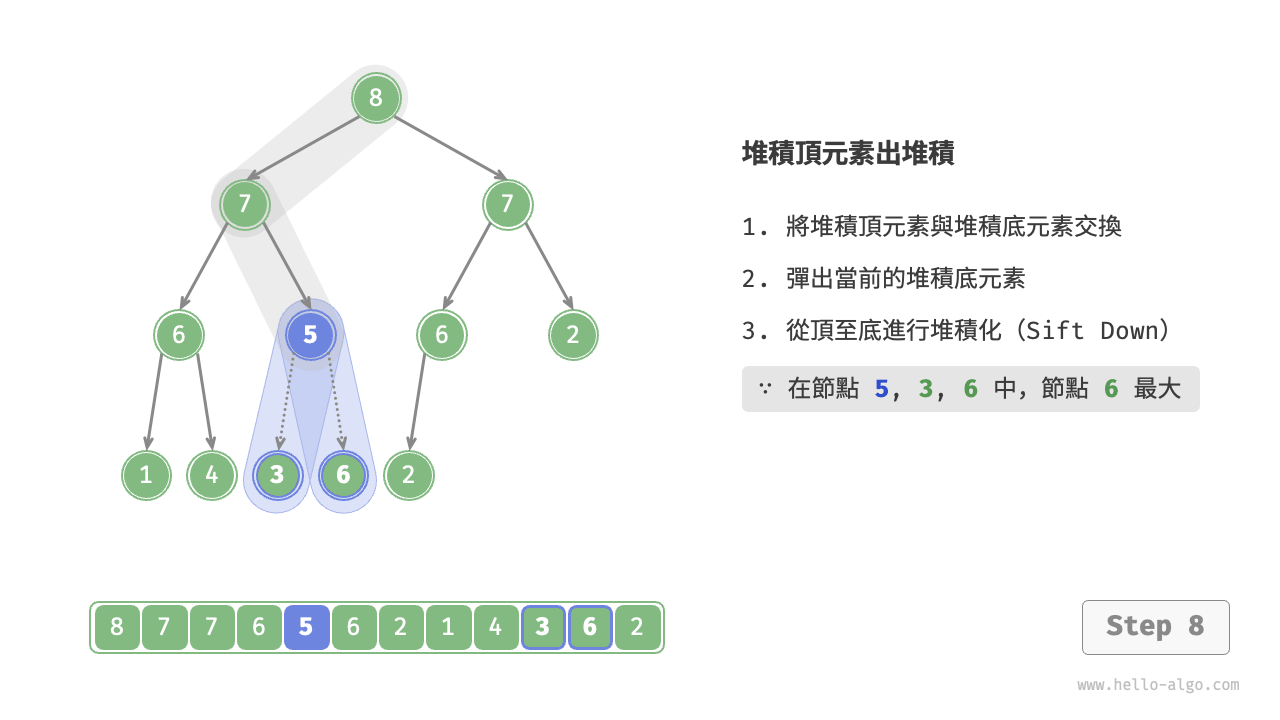
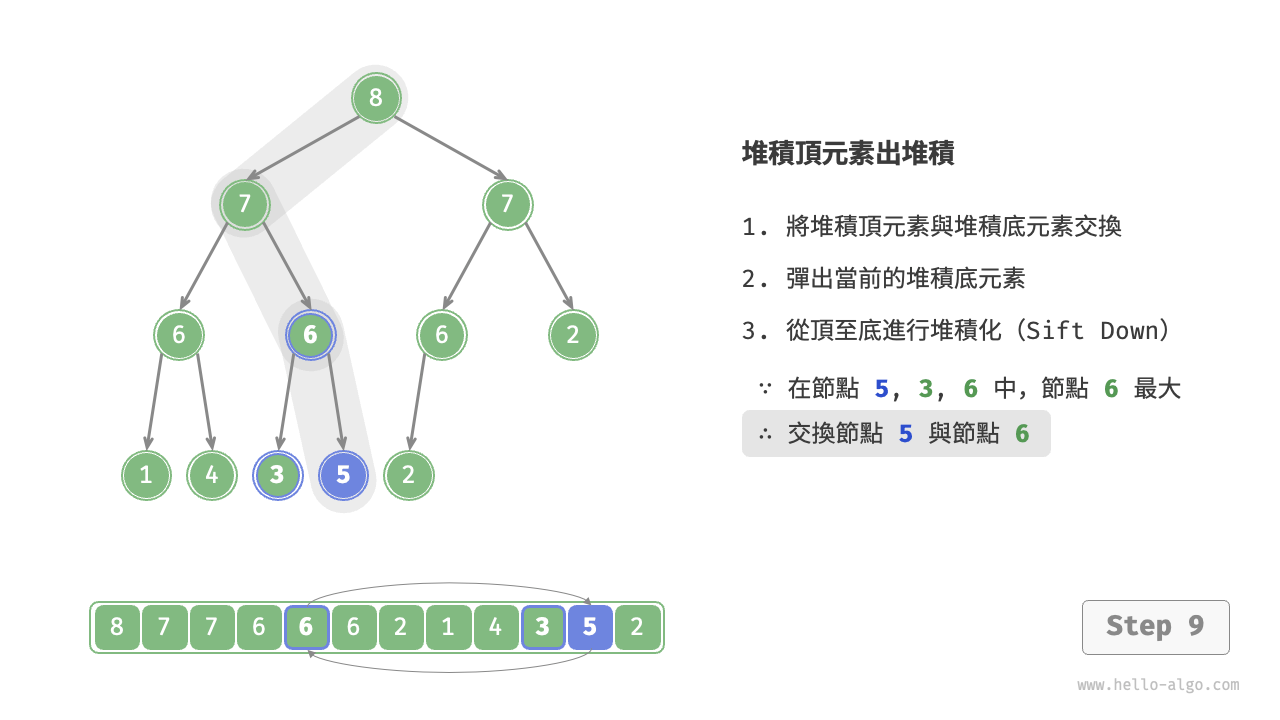
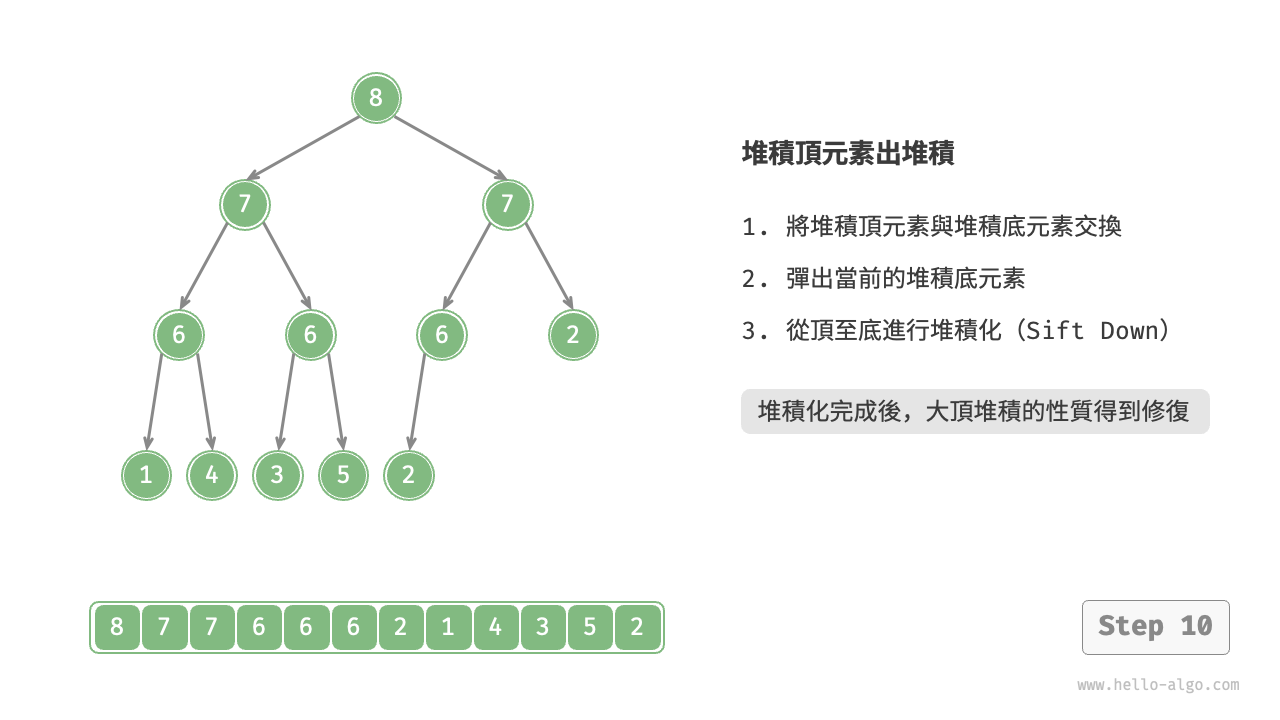
如下圖所示,“從頂至底堆積化”的操作方向與“從底至頂堆積化”相反,我們將根節點的值與其兩個子節點的值進行比較,將最大的子節點與根節點交換。然後迴圈執行此操作,直到越過葉節點或遇到無須交換的節點時結束。
與元素入堆積操作相似,堆積頂元素出堆積操作的時間複雜度也為 O(\log n) 。程式碼如下所示:
[file]{my_heap}-[class]{max_heap}-[func]{sift_down}
堆積的常見應用
- 優先佇列:堆積通常作為實現優先佇列的首選資料結構,其入列和出列操作的時間複雜度均為
O(\log n),而建堆積操作為O(n),這些操作都非常高效。 - 堆積排序:給定一組資料,我們可以用它們建立一個堆積,然後不斷地執行元素出堆積操作,從而得到有序資料。然而,我們通常會使用一種更優雅的方式實現堆積排序,詳見“堆積排序”章節。
- 獲取最大的
k個元素:這是一個經典的演算法問題,同時也是一種典型應用,例如選擇熱度前 10 的新聞作為微博熱搜,選取銷量前 10 的商品等。