7.7 KiB
哈希冲突
上节提到,通常情况下哈希函数的输入空间远大于输出空间,因此哈希冲突是不可避免的。例如,输入空间为全体整数,输出空间为数组容量大小,则必然有多个整数映射至同一数组索引。
哈希冲突会导致查询结果错误,严重影响哈希表的可用性。为解决该问题,我们可以每当遇到哈希冲突时就进行哈希表扩容,直至冲突消失为止。此方法简单粗暴且有效,但效率太低,因为哈希表扩容需要进行大量的数据搬运与哈希值计算。为了提升效率,我们换一种思路:
- 改良哈希表数据结构,使得哈希表可以在存在哈希冲突时正常工作。
- 仅在必要时,即当哈希冲突比较严重时,执行扩容操作。
哈希表的结构改良方法主要包括链式地址和开放寻址。
链式地址
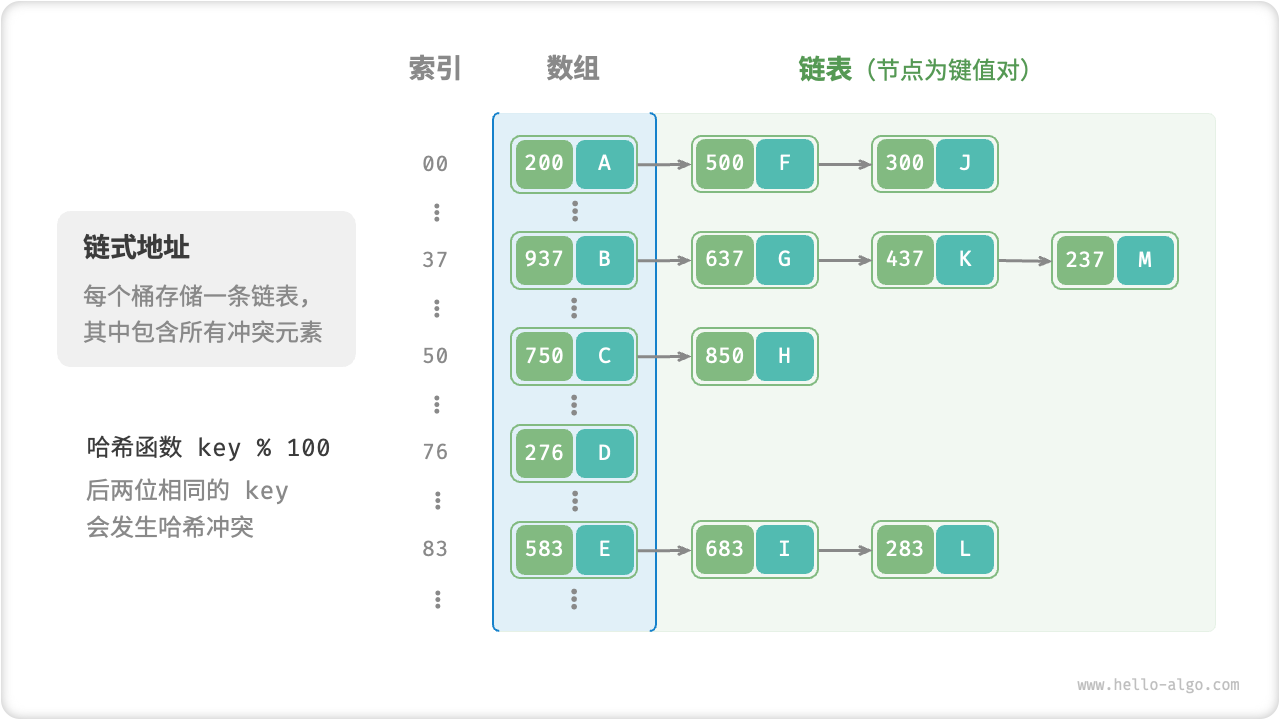
在原始哈希表中,每个桶仅能存储一个键值对。「链式地址 Separate Chaining」将单个元素转换为链表,将键值对作为链表节点,将所有发生冲突的键值对都存储在同一链表中。
链式地址下,哈希表的操作方法包括:
- 查询元素:输入
key,经过哈希函数得到数组索引,即可访问链表头节点,然后遍历链表并对比key以查找目标键值对。 - 添加元素:先通过哈希函数访问链表头节点,然后将节点(即键值对)添加到链表中。
- 删除元素:根据哈希函数的结果访问链表头部,接着遍历链表以查找目标节点,并将其删除。
该方法存在一些局限性,包括:
- 占用空间增大,由于链表或二叉树包含节点指针,相比数组更加耗费内存空间;
- 查询效率降低,因为需要线性遍历链表来查找对应元素;
以下给出了链式地址哈希表的简单实现,需要注意:
- 为了使得代码尽量简短,我们使用列表(动态数组)代替链表。换句话说,哈希表(数组)包含多个桶,每个桶都是一个列表。
- 以下代码实现了哈希表扩容方法。具体来看,当负载因子超过
0.75时,我们将哈希表扩容至2倍。
=== "Java"
```java title="hash_map_chaining.java"
[class]{HashMapChaining}-[func]{}
```
=== "C++"
```cpp title="hash_map_chaining.cpp"
[class]{HashMapChaining}-[func]{}
```
=== "Python"
```python title="hash_map_chaining.py"
[class]{HashMapChaining}-[func]{}
```
=== "Go"
```go title="hash_map_chaining.go"
[class]{hashMapChaining}-[func]{}
```
=== "JavaScript"
```javascript title="hash_map_chaining.js"
[class]{HashMapChaining}-[func]{}
```
=== "TypeScript"
```typescript title="hash_map_chaining.ts"
[class]{HashMapChaining}-[func]{}
```
=== "C"
```c title="hash_map_chaining.c"
[class]{hashMapChaining}-[func]{}
```
=== "C#"
```csharp title="hash_map_chaining.cs"
[class]{HashMapChaining}-[func]{}
```
=== "Swift"
```swift title="hash_map_chaining.swift"
[class]{HashMapChaining}-[func]{}
```
=== "Zig"
```zig title="hash_map_chaining.zig"
[class]{HashMapChaining}-[func]{}
```
=== "Dart"
```dart title="hash_map_chaining.dart"
[class]{HashMapChaining}-[func]{}
```
!!! tip
为了提高效率,**我们可以将链表转换为「AVL 树」或「红黑树」**,从而将查询操作的时间复杂度优化至 $O(\log n)$ 。
开放寻址
「开放寻址 Open Addressing」不引入额外的数据结构,而是通过“多次探测”来处理哈希冲突,探测方式主要包括线性探测、平方探测、多次哈希。
线性探测
线性探测采用固定步长的线性查找来进行探测,对应的哈希表操作方法为:
- 插入元素:通过哈希函数计算数组索引,若发现桶内已有元素,则从冲突位置向后线性遍历(步长通常为
1),直至找到空位,将元素插入其中。 - 查找元素:若发现哈希冲突,则使用相同步长向后线性遍历,直到找到对应元素,返回
value即可;或者若遇到空位,说明目标键值对不在哈希表中,返回\text{None}。
然而,线性探测存在以下缺陷:
- 不能直接删除元素。删除元素会在数组内产生一个空位,查找其他元素时,该空位可能导致程序误判元素不存在。因此,需要借助一个标志位来标记已删除元素。
- 容易产生聚集。数组内连续被占用位置越长,这些连续位置发生哈希冲突的可能性越大,进一步促使这一位置的“聚堆生长”,最终导致增删查改操作效率降低。
如以下代码所示,为开放寻址(线性探测)哈希表的简单实现,重点包括:
- 我们使用一个固定的键值对实例
removed来标记已删除元素。也就是说,当一个桶为\text{None}或removed时,这个桶都是空的,可用于放置键值对。 - 被标记为已删除的空间是可以再次被使用的。当插入元素时,若通过哈希函数找到了被标记为已删除的索引,则可将该元素放置到该索引。
- 在线性探测时,我们从当前索引
index向后遍历;而当越过数组尾部时,需要回到头部继续遍历。
=== "Java"
```java title="hash_map_open_addressing.java"
[class]{HashMapOpenAddressing}-[func]{}
```
=== "C++"
```cpp title="hash_map_open_addressing.cpp"
[class]{HashMapOpenAddressing}-[func]{}
```
=== "Python"
```python title="hash_map_open_addressing.py"
[class]{HashMapOpenAddressing}-[func]{}
```
=== "Go"
```go title="hash_map_open_addressing.go"
[class]{hashMapOpenAddressing}-[func]{}
```
=== "JavaScript"
```javascript title="hash_map_open_addressing.js"
[class]{HashMapOpenAddressing}-[func]{}
```
=== "TypeScript"
```typescript title="hash_map_open_addressing.ts"
[class]{HashMapOpenAddressing}-[func]{}
```
=== "C"
```c title="hash_map_open_addressing.c"
[class]{hashMapOpenAddressing}-[func]{}
```
=== "C#"
```csharp title="hash_map_open_addressing.cs"
[class]{HashMapOpenAddressing}-[func]{}
```
=== "Swift"
```swift title="hash_map_open_addressing.swift"
[class]{HashMapOpenAddressing}-[func]{}
```
=== "Zig"
```zig title="hash_map_open_addressing.zig"
[class]{HashMapOpenAddressing}-[func]{}
```
=== "Dart"
```dart title="hash_map_open_addressing.dart"
[class]{HashMapOpenAddressing}-[func]{}
```
多次哈希
顾名思义,多次哈希方法是使用多个哈希函数 f_1(x) , f_2(x) , f_3(x) , \cdots 进行探测。
- 插入元素:若哈希函数
f_1(x)出现冲突,则尝试f_2(x),以此类推,直到找到空位后插入元素。 - 查找元素:在相同的哈希函数顺序下进行查找,直到找到目标元素时返回;或遇到空位或已尝试所有哈希函数,说明哈希表中不存在该元素,则返回
\text{None}。
与线性探测相比,多次哈希方法不易产生聚集,但多个哈希函数会增加额外的计算量。
!!! note "编程语言的选择"
Java 采用链式地址。自 JDK 1.8 以来,当 HashMap 内数组长度达到 64 且链表长度达到 8 时,链表会被转换为红黑树以提升查找性能。
Python 采用开放寻址。字典 dict 使用伪随机数进行探测。
Golang 采用链式地址。Go 规定每个桶最多存储 8 个键值对,超出容量则连接一个溢出桶;当溢出桶过多时,会执行一次特殊的等量扩容操作,以确保性能。