11 KiB
Executable file
队列
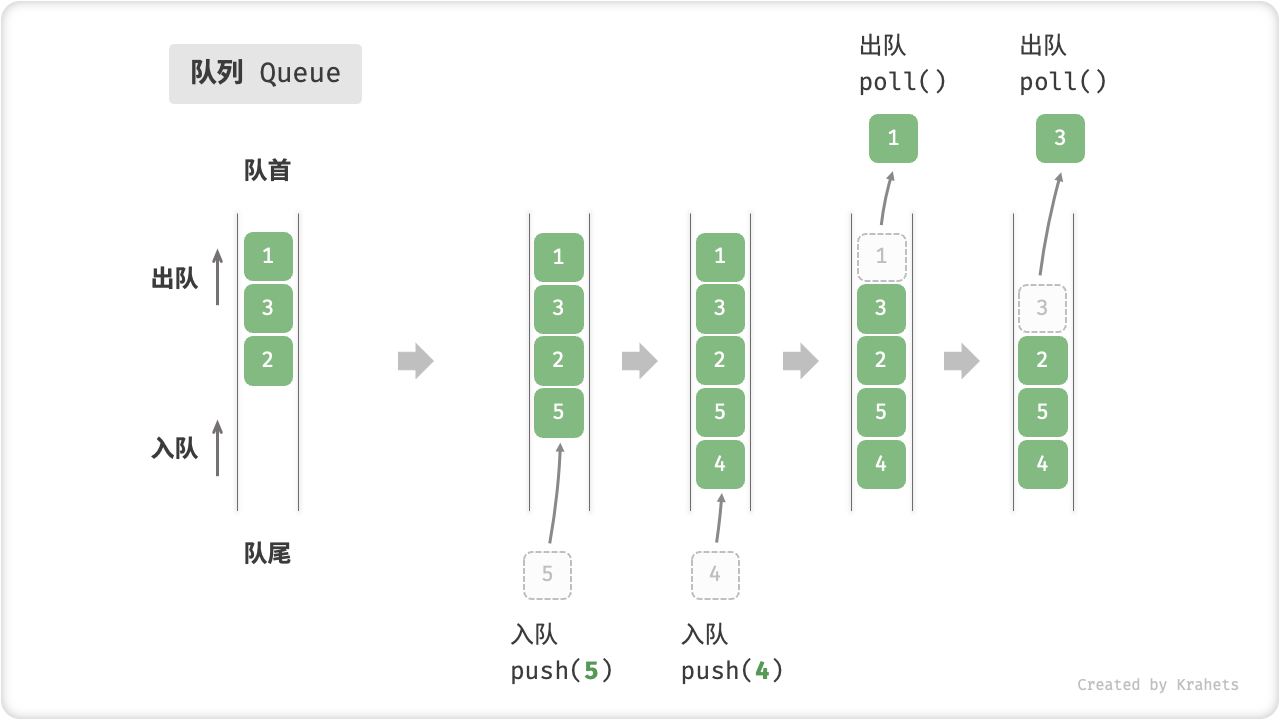
「队列 Queue」是一种遵循「先入先出 first in, first out」数据操作规则的线性数据结构。顾名思义,队列模拟的是排队现象,即外面的人不断加入队列尾部,而处于队列头部的人不断地离开。
我们将队列头部称为「队首」,队列尾部称为「队尾」,将把元素加入队尾的操作称为「入队」,删除队首元素的操作称为「出队」。
队列常用操作
队列的常用操作见下表,方法名需根据特定语言来确定。
| 方法名 | 描述 | 时间复杂度 |
|---|---|---|
| push() | 元素入队,即将元素添加至队尾 | O(1) |
| poll() | 队首元素出队 | O(1) |
| front() | 访问队首元素 | O(1) |
| size() | 获取队列的长度 | O(1) |
| isEmpty() | 判断队列是否为空 | O(1) |
我们可以直接使用编程语言实现好的队列类。
=== "Java"
```java title="queue.java"
/* 初始化队列 */
Queue<Integer> queue = new LinkedList<>();
/* 元素入队 */
queue.offer(1);
queue.offer(3);
queue.offer(2);
queue.offer(5);
queue.offer(4);
/* 访问队首元素 */
int peek = queue.peek();
/* 元素出队 */
int poll = queue.poll();
/* 获取队列的长度 */
int size = queue.size();
/* 判断队列是否为空 */
boolean isEmpty = queue.isEmpty();
```
=== "C++"
```cpp title="queue.cpp"
/* 初始化队列 */
queue<int> queue;
/* 元素入队 */
queue.push(1);
queue.push(3);
queue.push(2);
queue.push(5);
queue.push(4);
/* 访问队首元素 */
int front = queue.front();
/* 元素出队 */
queue.pop();
/* 获取队列的长度 */
int size = queue.size();
/* 判断队列是否为空 */
bool empty = queue.empty();
```
=== "Python"
```python title="queue.py"
""" 初始化队列 """
# 在 Python 中,我们一般将双向队列类 deque 看作队列使用
# 虽然 queue.Queue() 是纯正的队列类,但不太好用,因此不建议
que = collections.deque()
""" 元素入队 """
que.append(1)
que.append(3)
que.append(2)
que.append(5)
que.append(4)
""" 访问队首元素 """
front = que[0];
""" 元素出队 """
pop = que.popleft()
""" 获取队列的长度 """
size = len(que)
""" 判断队列是否为空 """
is_empty = len(que) == 0
```
=== "Go"
```go title="queue_test.go"
/* 初始化队列 */
// 在 Go 中,将 list 作为队列来使用
queue := list.New()
/* 元素入队 */
queue.PushBack(1)
queue.PushBack(3)
queue.PushBack(2)
queue.PushBack(5)
queue.PushBack(4)
/* 访问队首元素 */
peek := queue.Front()
/* 元素出队 */
poll := queue.Front()
queue.Remove(poll)
/* 获取队列的长度 */
size := queue.Len()
/* 判断队列是否为空 */
isEmpty := queue.Len() == 0
```
=== "JavaScript"
```javascript title="queue.js"
/* 初始化队列 */
// JavaScript 没有内置的队列,可以把 Array 当作队列来使用
const queue = [];
/* 元素入队 */
queue.push(1);
queue.push(3);
queue.push(2);
queue.push(5);
queue.push(4);
/* 访问队首元素 */
const peek = queue[0];
/* 元素出队 */
// 底层是数组,因此 shift() 方法的时间复杂度为 O(n)
const poll = queue.shift();
/* 获取队列的长度 */
const size = queue.length;
/* 判断队列是否为空 */
const empty = queue.length === 0;
```
=== "TypeScript"
```typescript title="queue.ts"
/* 初始化队列 */
// TypeScript 没有内置的队列,可以把 Array 当作队列来使用
const queue: number[] = [];
/* 元素入队 */
queue.push(1);
queue.push(3);
queue.push(2);
queue.push(5);
queue.push(4);
/* 访问队首元素 */
const peek = queue[0];
/* 元素出队 */
// 底层是数组,因此 shift() 方法的时间复杂度为 O(n)
const poll = queue.shift();
/* 获取队列的长度 */
const size = queue.length;
/* 判断队列是否为空 */
const empty = queue.length === 0;
```
=== "C"
```c title="queue.c"
```
=== "C#"
```csharp title="queue.cs"
/* 初始化队列 */
Queue<int> queue = new();
/* 元素入队 */
queue.Enqueue(1);
queue.Enqueue(3);
queue.Enqueue(2);
queue.Enqueue(5);
queue.Enqueue(4);
/* 访问队首元素 */
int peek = queue.Peek();
/* 元素出队 */
int poll = queue.Dequeue();
/* 获取队列的长度 */
int size = queue.Count();
/* 判断队列是否为空 */
bool isEmpty = queue.Count() == 0;
```
=== "Swift"
```swift title="queue.swift"
/* 初始化队列 */
// Swift 没有内置的队列类,可以把 Array 当作队列来使用
var queue: [Int] = []
/* 元素入队 */
queue.append(1)
queue.append(3)
queue.append(2)
queue.append(5)
queue.append(4)
/* 访问队首元素 */
let peek = queue.first!
/* 元素出队 */
// 使用 Array 模拟时 poll 的复杂度为 O(n)
let pool = queue.removeFirst()
/* 获取队列的长度 */
let size = queue.count
/* 判断队列是否为空 */
let isEmpty = queue.isEmpty
```
=== "Zig"
```zig title="queue.zig"
```
队列实现
队列需要一种可以在一端添加,并在另一端删除的数据结构,也可以使用链表或数组来实现。
基于链表的实现
我们将链表的「头结点」和「尾结点」分别看作是队首和队尾,并规定队尾只可添加结点,队首只可删除结点。
以下是使用链表实现队列的示例代码。
=== "Java"
```java title="linkedlist_queue.java"
[class]{LinkedListQueue}-[func]{}
```
=== "C++"
```cpp title="linkedlist_queue.cpp"
[class]{LinkedListQueue}-[func]{}
```
=== "Python"
```python title="linkedlist_queue.py"
[class]{LinkedListQueue}-[func]{}
```
=== "Go"
```go title="linkedlist_queue.go"
[class]{linkedListQueue}-[func]{}
```
=== "JavaScript"
```javascript title="linkedlist_queue.js"
[class]{LinkedListQueue}-[func]{}
```
=== "TypeScript"
```typescript title="linkedlist_queue.ts"
[class]{LinkedListQueue}-[func]{}
```
=== "C"
```c title="linkedlist_queue.c"
[class]{linkedListQueue}-[func]{}
```
=== "C#"
```csharp title="linkedlist_queue.cs"
[class]{LinkedListQueue}-[func]{}
```
=== "Swift"
```swift title="linkedlist_queue.swift"
[class]{LinkedListQueue}-[func]{}
```
=== "Zig"
```zig title="linkedlist_queue.zig"
[class]{LinkedListQueue}-[func]{}
```
基于数组的实现
数组的删除首元素的时间复杂度为 O(n) ,这会导致出队操作效率低下。然而,我们可以采取下述的巧妙方法来避免这个问题。
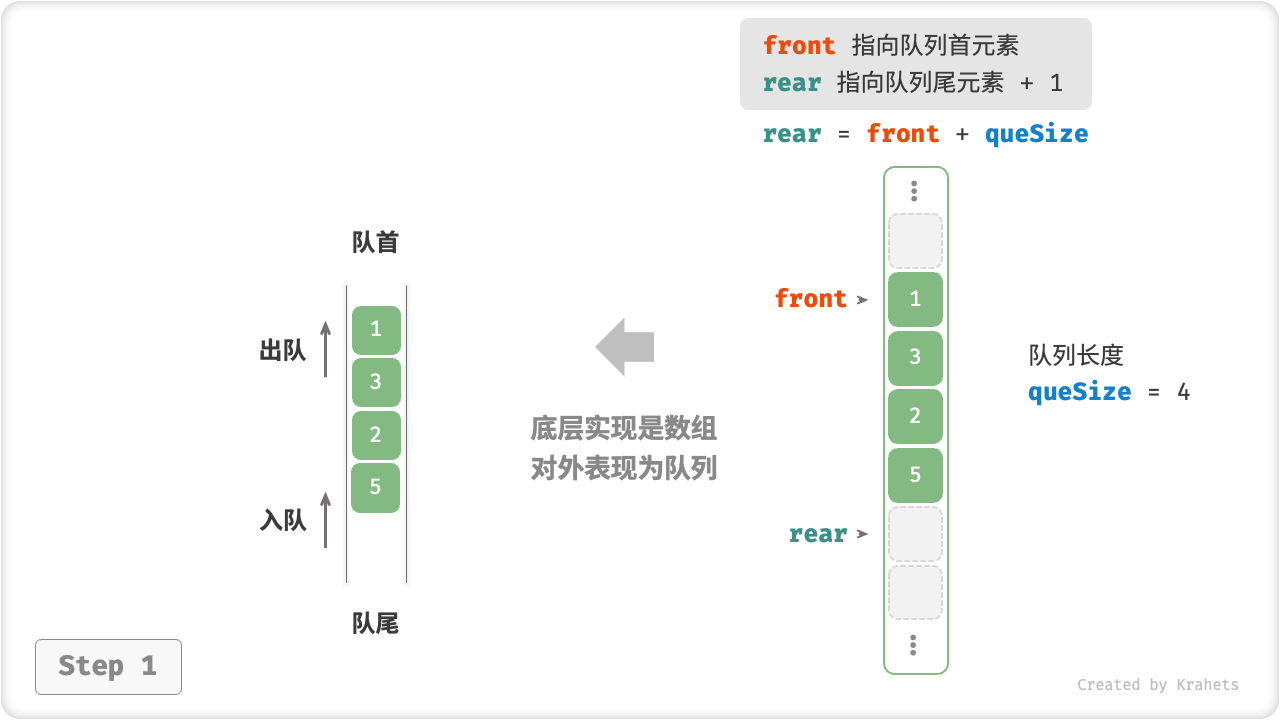
考虑借助一个变量 front 来指向队首元素的索引,并维护变量 queSize 来记录队列长度。我们定义 rear = front + queSize ,该公式计算出来的 rear 指向“队尾元素索引 +1 ”的位置。
在该设计下,数组中包含元素的有效区间为 [front, rear - 1] ,进而
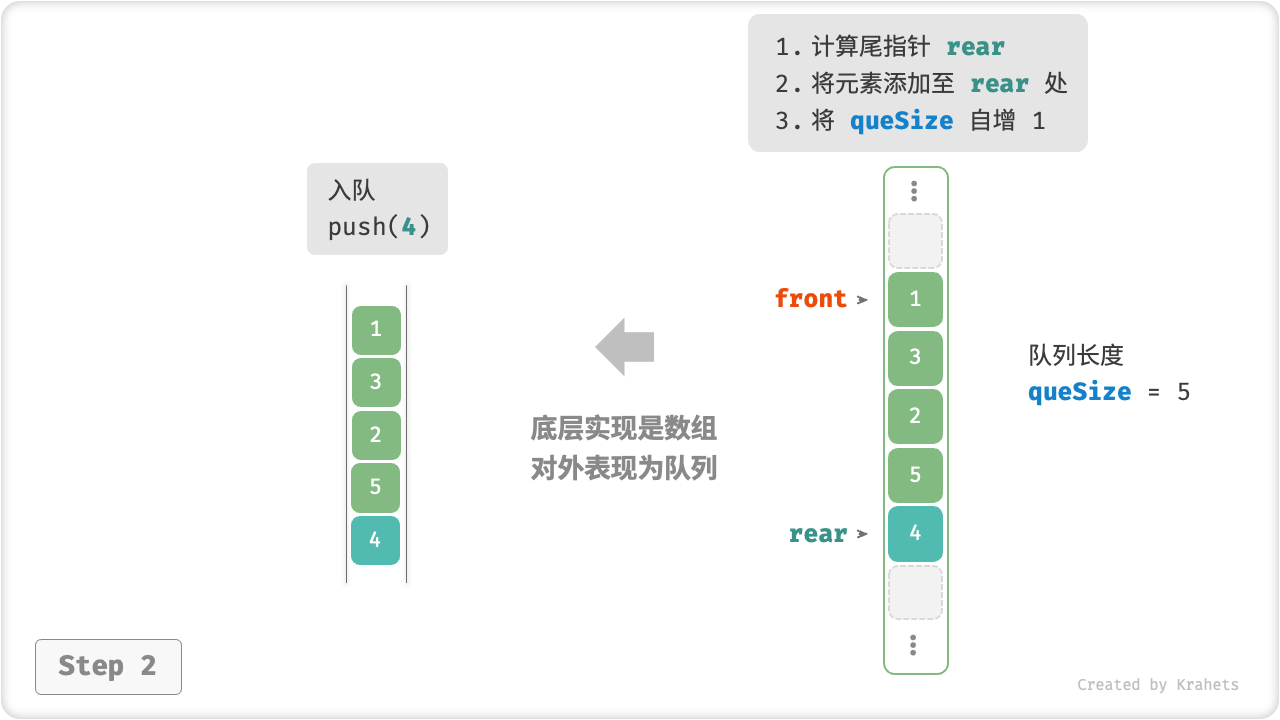
- 对于入队操作,将输入元素赋值给
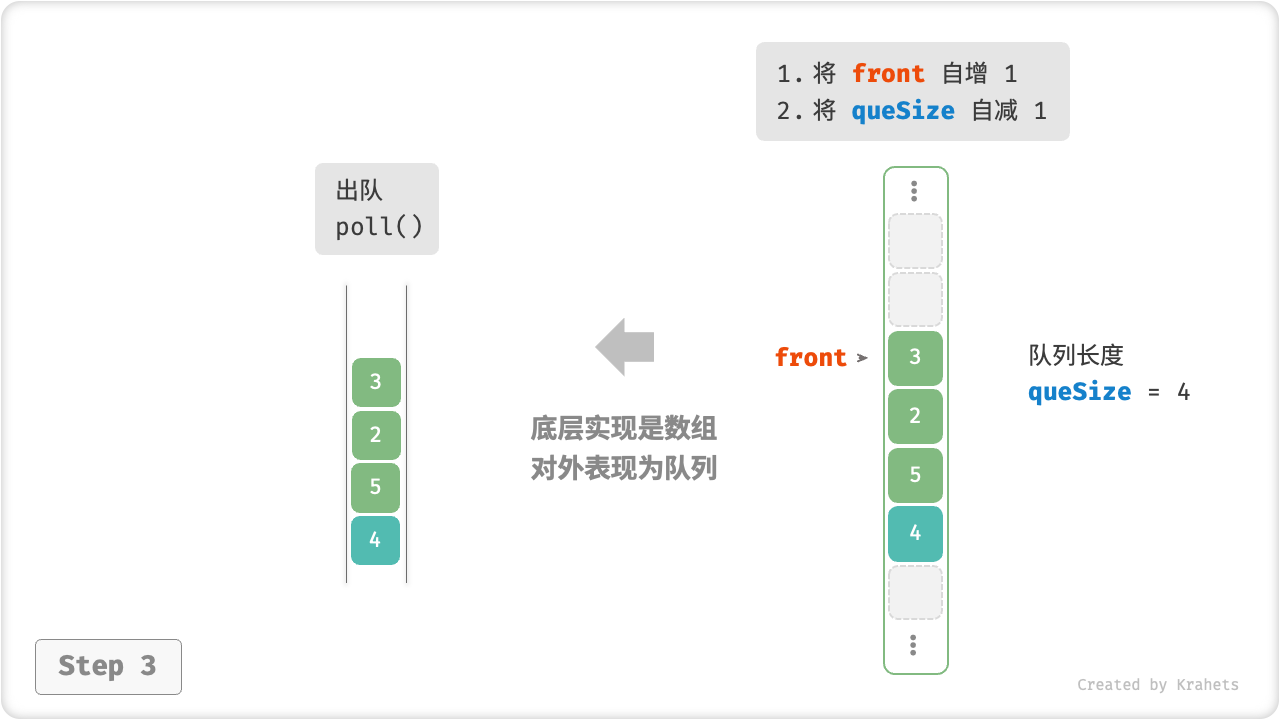
rear索引处,并将queSize自增1即可; - 对于出队操作,仅需将
front自增1,并将queSize自减1即可;
观察发现,入队与出队操作都仅需单次操作即可完成,时间复杂度皆为 O(1) 。
细心的同学可能会发现一个问题:在不断入队与出队的过程中,front 和 rear 都在向右移动,在到达数组尾部后就无法继续移动了。为解决此问题,我们考虑将数组看作是首尾相接的,这样的数组被称为「环形数组」。
对于环形数组,我们需要令 front 或 rear 在越过数组尾部后,直接绕回到数组头部接续遍历。这种周期性规律可以通过「取余操作」来实现,详情请见以下代码。
=== "Java"
```java title="array_queue.java"
[class]{ArrayQueue}-[func]{}
```
=== "C++"
```cpp title="array_queue.cpp"
[class]{ArrayQueue}-[func]{}
```
=== "Python"
```python title="array_queue.py"
[class]{ArrayQueue}-[func]{}
```
=== "Go"
```go title="array_queue.go"
[class]{arrayQueue}-[func]{}
```
=== "JavaScript"
```javascript title="array_queue.js"
[class]{ArrayQueue}-[func]{}
```
=== "TypeScript"
```typescript title="array_queue.ts"
[class]{ArrayQueue}-[func]{}
```
=== "C"
```c title="array_queue.c"
[class]{arrayQueue}-[func]{}
```
=== "C#"
```csharp title="array_queue.cs"
[class]{ArrayQueue}-[func]{}
```
=== "Swift"
```swift title="array_queue.swift"
[class]{ArrayQueue}-[func]{}
```
=== "Zig"
```zig title="array_queue.zig"
[class]{ArrayQueue}-[func]{}
```
以上实现的队列仍存在局限性,即长度不可变。不过这个问题很容易解决,我们可以将数组替换为列表(即动态数组),从而引入扩容机制。有兴趣的同学可以尝试自行实现。
两种实现对比
与栈的结论一致,在此不再赘述。
队列典型应用
- 淘宝订单。购物者下单后,订单就被加入到队列之中,随后系统再根据顺序依次处理队列中的订单。在双十一时,在短时间内会产生海量的订单,如何处理「高并发」则是工程师们需要重点思考的问题。
- 各种待办事项。任何需要实现“先来后到”的功能,例如打印机的任务队列、餐厅的出餐队列等等。