7.6 KiB
Executable file
二分查找
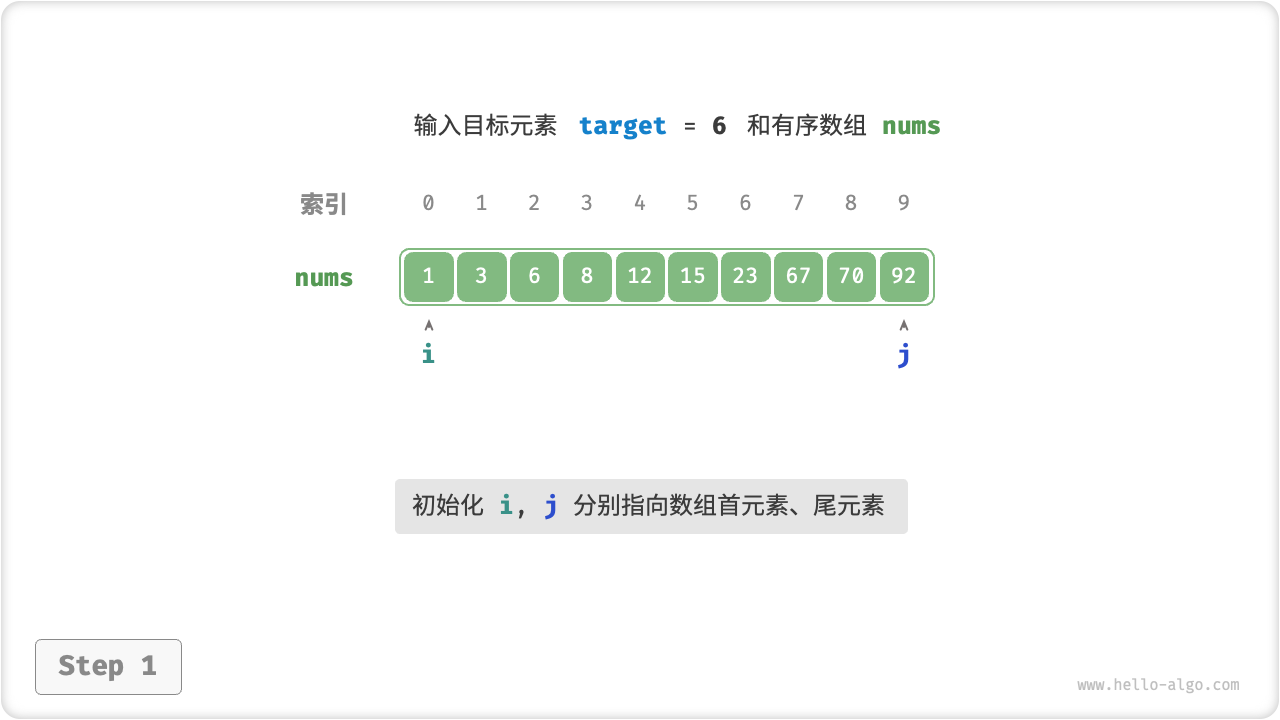
「二分查找 Binary Search」利用数据的有序性,通过每轮减少一半搜索范围来定位目标元素。
算法实现
给定一个长度为 n 的有序数组 nums ,元素按从小到大的顺序排列。数组索引的取值范围为:
$$
0, 1, 2, \cdots, n-1
我们通常使用以下两种方法来表示这个取值范围:
- 双闭区间 $[0, n-1]$ ,即两个边界都包含自身;在此方法下,区间
[0, 0]仍包含1个元素; - 左闭右开 $[0, n)$ ,即左边界包含自身、右边界不包含自身;在此方法下,区间
[0, 0)不包含元素;
“双闭区间”实现
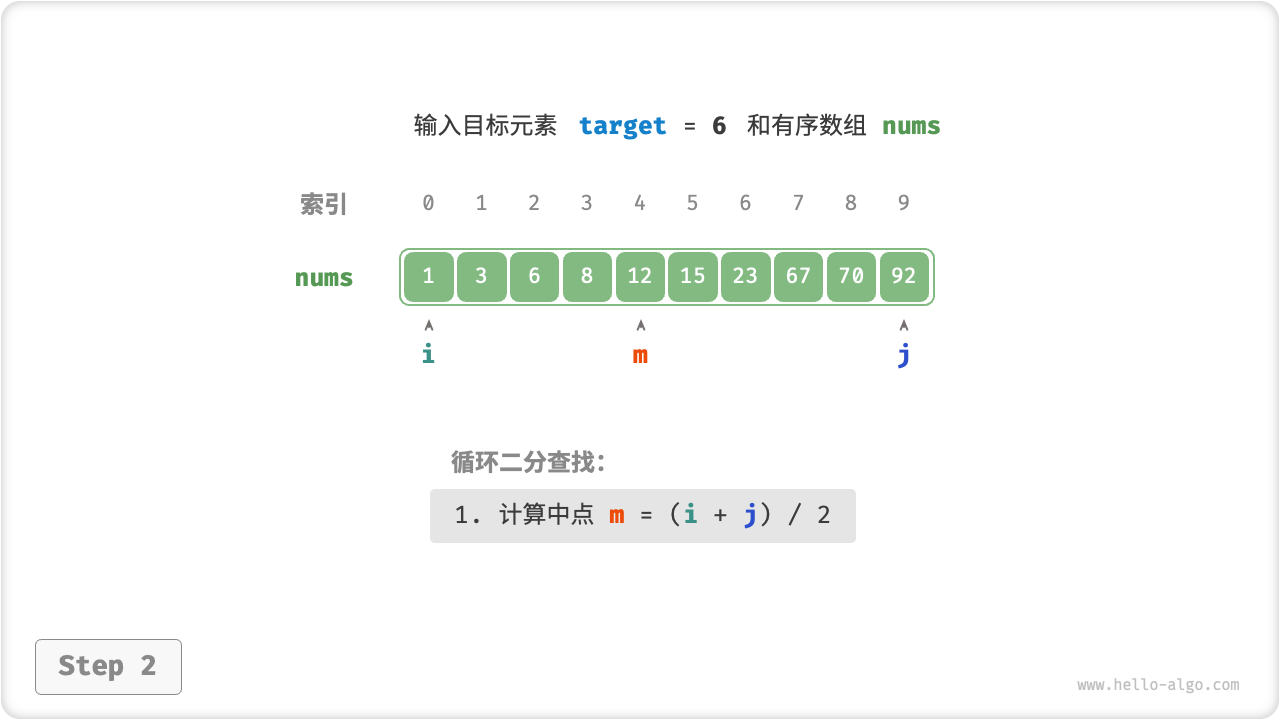
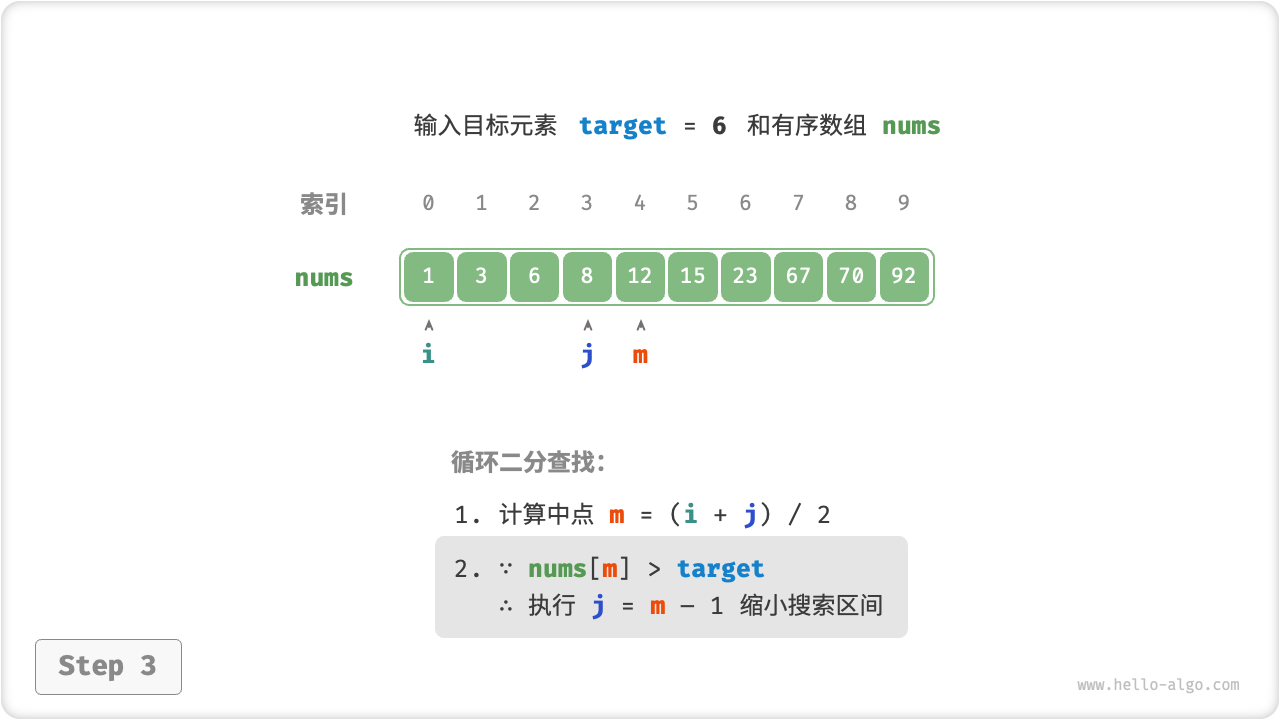
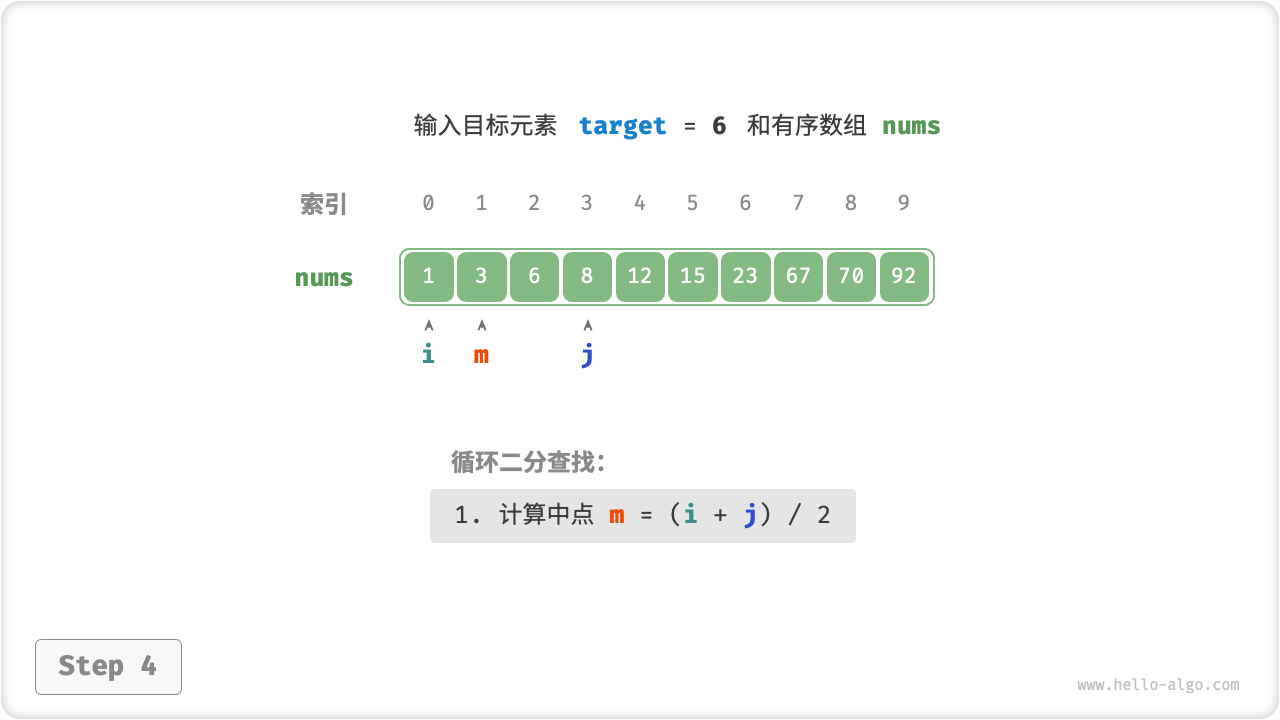
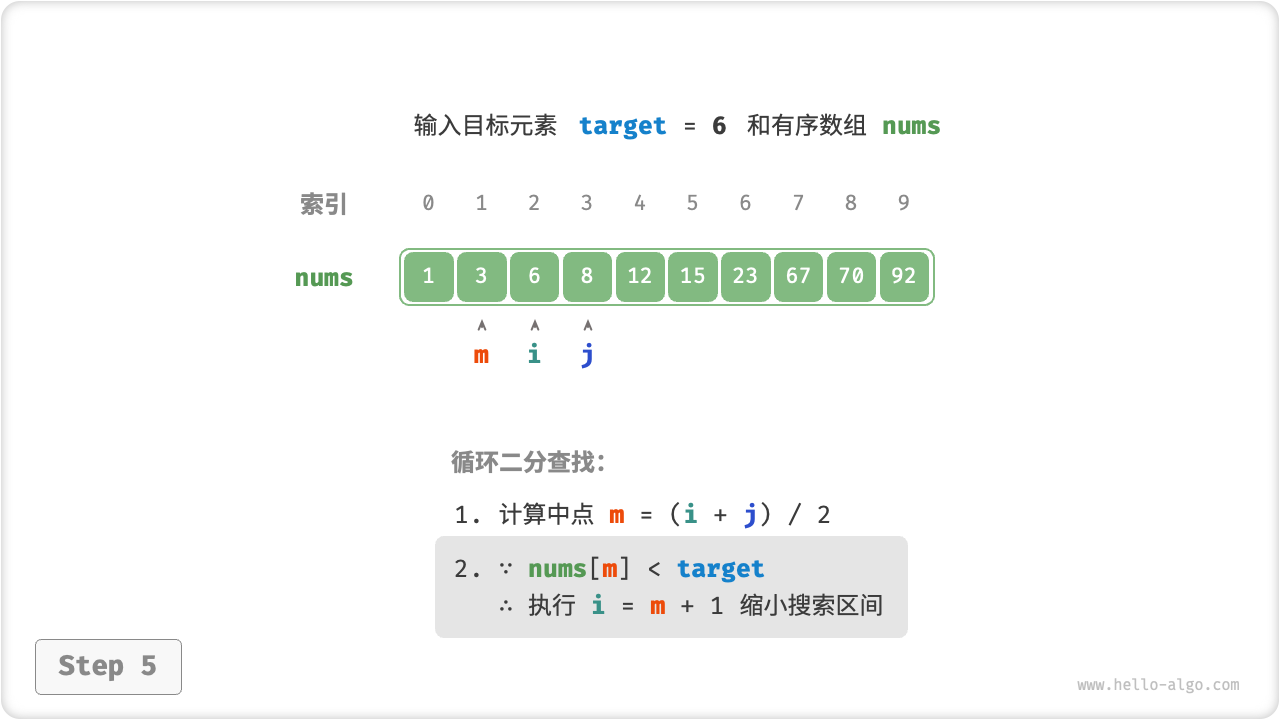
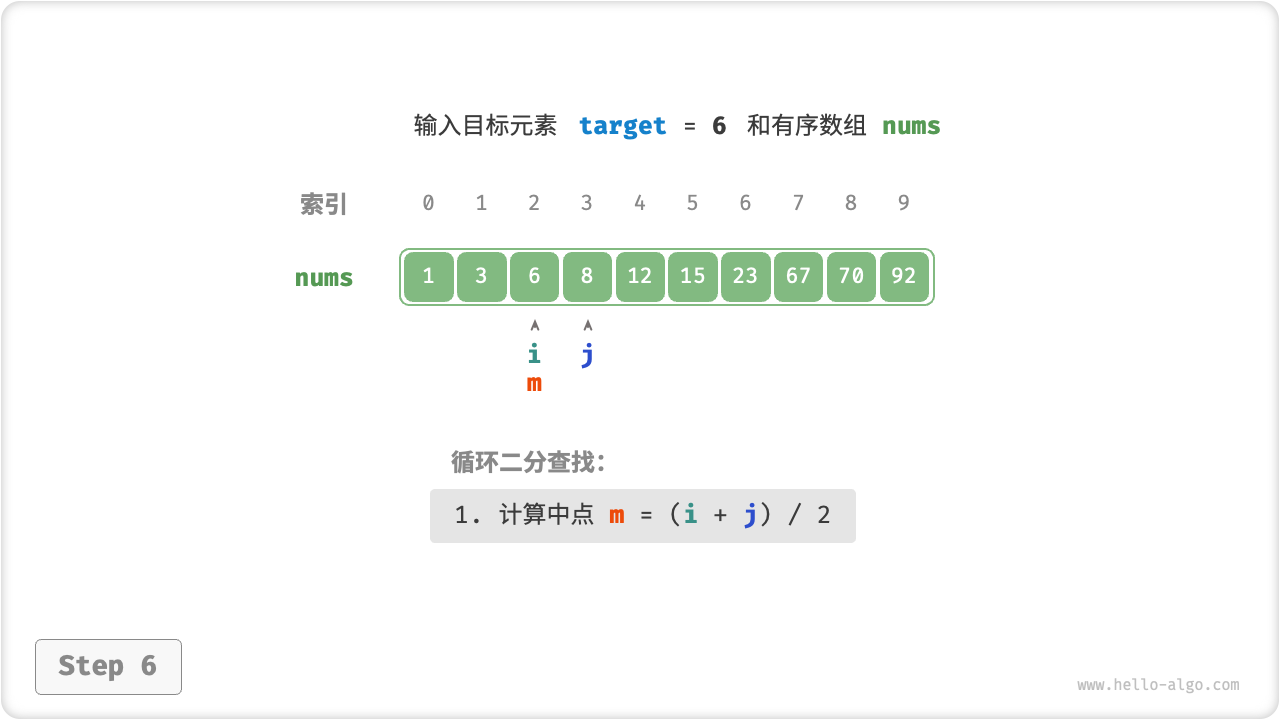
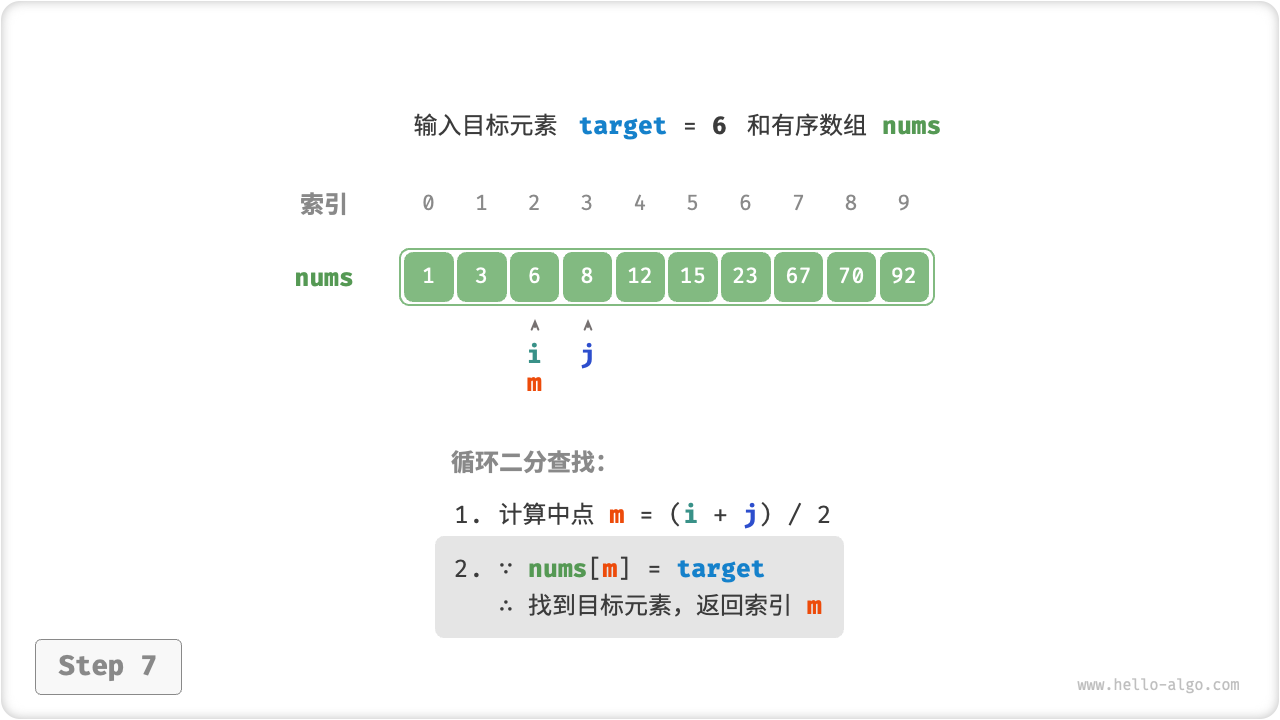
首先,我们采用“双闭区间”表示法,在数组 nums 中查找目标元素 target 的对应索引。
二分查找在“双闭区间”表示下的代码如下所示。
=== "Java"
```java title="binary_search.java"
[class]{binary_search}-[func]{binarySearch}
```
=== "C++"
```cpp title="binary_search.cpp"
[class]{}-[func]{binarySearch}
```
=== "Python"
```python title="binary_search.py"
[class]{}-[func]{binary_search}
```
=== "Go"
```go title="binary_search.go"
[class]{}-[func]{binarySearch}
```
=== "JavaScript"
```javascript title="binary_search.js"
[class]{}-[func]{binarySearch}
```
=== "TypeScript"
```typescript title="binary_search.ts"
[class]{}-[func]{binarySearch}
```
=== "C"
```c title="binary_search.c"
[class]{}-[func]{binarySearch}
```
=== "C#"
```csharp title="binary_search.cs"
[class]{binary_search}-[func]{binarySearch}
```
=== "Swift"
```swift title="binary_search.swift"
[class]{}-[func]{binarySearch}
```
=== "Zig"
```zig title="binary_search.zig"
[class]{}-[func]{binarySearch}
```
“左闭右开”实现
此外,我们也可以采用“左闭右开”的表示法,编写具有相同功能的二分查找代码。
=== "Java"
```java title="binary_search.java"
[class]{binary_search}-[func]{binarySearch1}
```
=== "C++"
```cpp title="binary_search.cpp"
[class]{}-[func]{binarySearch1}
```
=== "Python"
```python title="binary_search.py"
[class]{}-[func]{binary_search1}
```
=== "Go"
```go title="binary_search.go"
[class]{}-[func]{binarySearch1}
```
=== "JavaScript"
```javascript title="binary_search.js"
[class]{}-[func]{binarySearch1}
```
=== "TypeScript"
```typescript title="binary_search.ts"
[class]{}-[func]{binarySearch1}
```
=== "C"
```c title="binary_search.c"
[class]{}-[func]{binarySearch1}
```
=== "C#"
```csharp title="binary_search.cs"
[class]{binary_search}-[func]{binarySearch1}
```
=== "Swift"
```swift title="binary_search.swift"
[class]{}-[func]{binarySearch1}
```
=== "Zig"
```zig title="binary_search.zig"
[class]{}-[func]{binarySearch1}
```
两种表示对比
对比这两种代码写法,我们可以发现以下不同点:
| 表示方法 | 初始化指针 | 缩小区间 | 循环终止条件 |
|---|---|---|---|
双闭区间 [0, n-1] |
i = 0 , j = n-1 |
i = m + 1 , j = m - 1 |
i > j |
左闭右开 [0, n) |
i = 0 , j = n |
i = m + 1 , j = m |
i = j |
在“双闭区间”表示法中,由于对左右两边界的定义相同,因此缩小区间的 i 和 j 的处理方法也是对称的,这样更不容易出错。因此,建议采用“双闭区间”的写法。
大数越界处理
当数组长度非常大时,加法 i + j 的结果可能会超出 int 类型的取值范围。在这种情况下,我们需要采用一种更安全的计算中点的方法。
=== "Java"
```java title=""
// (i + j) 有可能超出 int 的取值范围
int m = (i + j) / 2;
// 更换为此写法则不会越界
int m = i + (j - i) / 2;
```
=== "C++"
```cpp title=""
// (i + j) 有可能超出 int 的取值范围
int m = (i + j) / 2;
// 更换为此写法则不会越界
int m = i + (j - i) / 2;
```
=== "Python"
```py title=""
# Python 中的数字理论上可以无限大(取决于内存大小)
# 因此无需考虑大数越界问题
```
=== "Go"
```go title=""
// (i + j) 有可能超出 int 的取值范围
m := (i + j) / 2
// 更换为此写法则不会越界
m := i + (j - i) / 2
```
=== "JavaScript"
```javascript title=""
// (i + j) 有可能超出 int 的取值范围
let m = parseInt((i + j) / 2);
// 更换为此写法则不会越界
let m = parseInt(i + (j - i) / 2);
```
=== "TypeScript"
```typescript title=""
// (i + j) 有可能超出 Number 的取值范围
let m = Math.floor((i + j) / 2);
// 更换为此写法则不会越界
let m = Math.floor(i + (j - i) / 2);
```
=== "C"
```c title=""
```
=== "C#"
```csharp title=""
// (i + j) 有可能超出 int 的取值范围
int m = (i + j) / 2;
// 更换为此写法则不会越界
int m = i + (j - i) / 2;
```
=== "Swift"
```swift title=""
// (i + j) 有可能超出 int 的取值范围
let m = (i + j) / 2
// 更换为此写法则不会越界
let m = i + (j - 1) / 2
```
=== "Zig"
```zig title=""
```
复杂度分析
时间复杂度 $O(\log n)$ :其中 n 为数组长度;每轮排除一半的区间,因此循环轮数为 \log_2 n ,使用 O(\log n) 时间。
空间复杂度 $O(1)$ :指针 i , j 使用常数大小空间。
优点与局限性
二分查找效率很高,主要体现在:
- 二分查找的时间复杂度较低。对数阶在大数据量情况下具有显著优势。例如,当数据大小
n = 2^{20}时,线性查找需要2^{20} = 1048576轮循环,而二分查找仅需\log_2 2^{20} = 20轮循环。 - 二分查找无需额外空间。与哈希查找相比,二分查找更加节省空间。
然而,并非所有情况下都可使用二分查找,原因如下:
- 二分查找仅适用于有序数据。若输入数据无序,为了使用二分查找而专门进行排序,得不偿失。因为排序算法的时间复杂度通常为
O(n \log n),比线性查找和二分查找都更高。对于频繁插入元素的场景,为保持数组有序性,需要将元素插入到特定位置,时间复杂度为O(n),也是非常昂贵的。 - 二分查找仅适用于数组。二分查找需要跳跃式(非连续地)访问元素,而在链表中执行跳跃式访问的效率较低,因此不适合应用在链表或基于链表实现的数据结构。
- 小数据量下,线性查找性能更佳。在线性查找中,每轮只需要 1 次判断操作;而在二分查找中,需要 1 次加法、1 次除法、1 ~ 3 次判断操作、1 次加法(减法),共 4 ~ 6 个单元操作;因此,当数据量
n较小时,线性查找反而比二分查找更快。