hello-algo/docs/chapter_graph/graph_traversal.md

图的遍历

!!! note "图与树的关系"

树代表的是“一对多”的关系，而图则具有更高的自由度，可以表示任意的“多对多”关系。因此，我们可以把树看作是图的一种特例。显然，**树的遍历操作也是图的遍历操作的一种特例**，建议你在学习本章节时融会贯通两者的概念与实现方法。

「图」和「树」都是非线性数据结构，都需要使用「搜索算法」来实现遍历操作。

与树类似，图的遍历方式也可分为两种，即「广度优先遍历 Breadth-First Traversal」和「深度优先遍历 Depth-First Traversal」，也称为「广度优先搜索 Breadth-First Search」和「深度优先搜索 Depth-First Search」，简称 BFS 和 DFS。

广度优先遍历

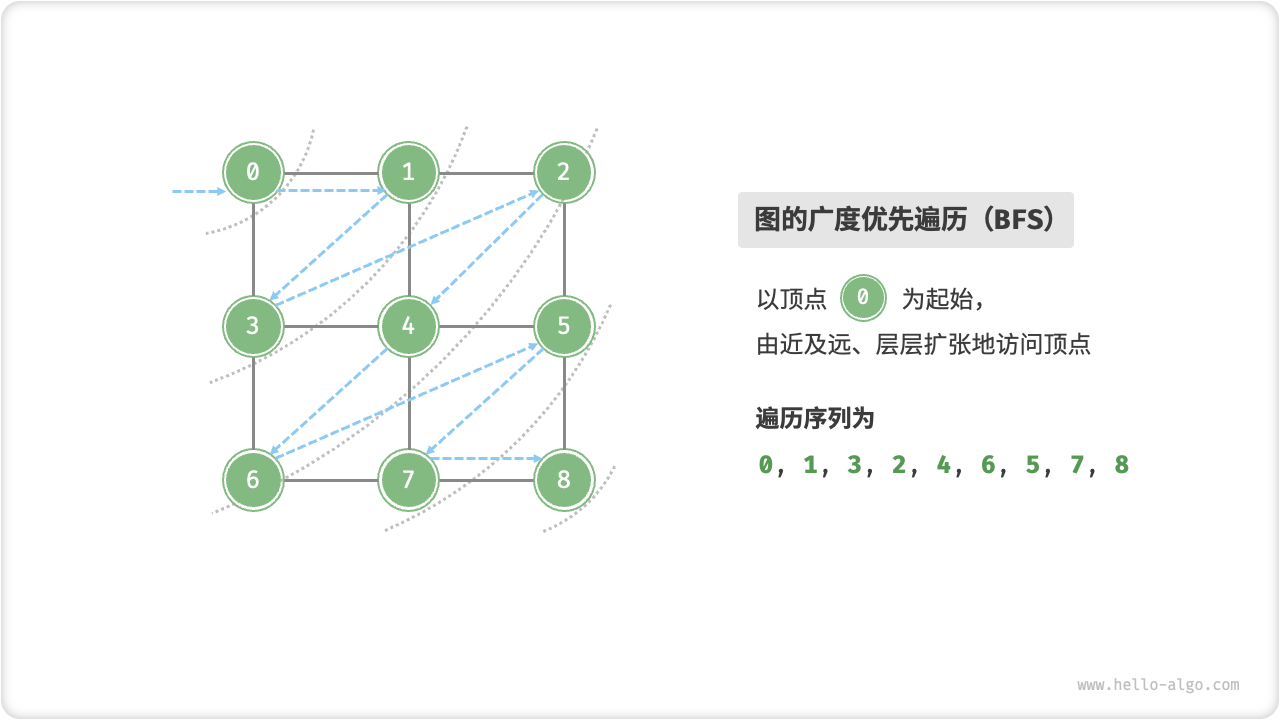
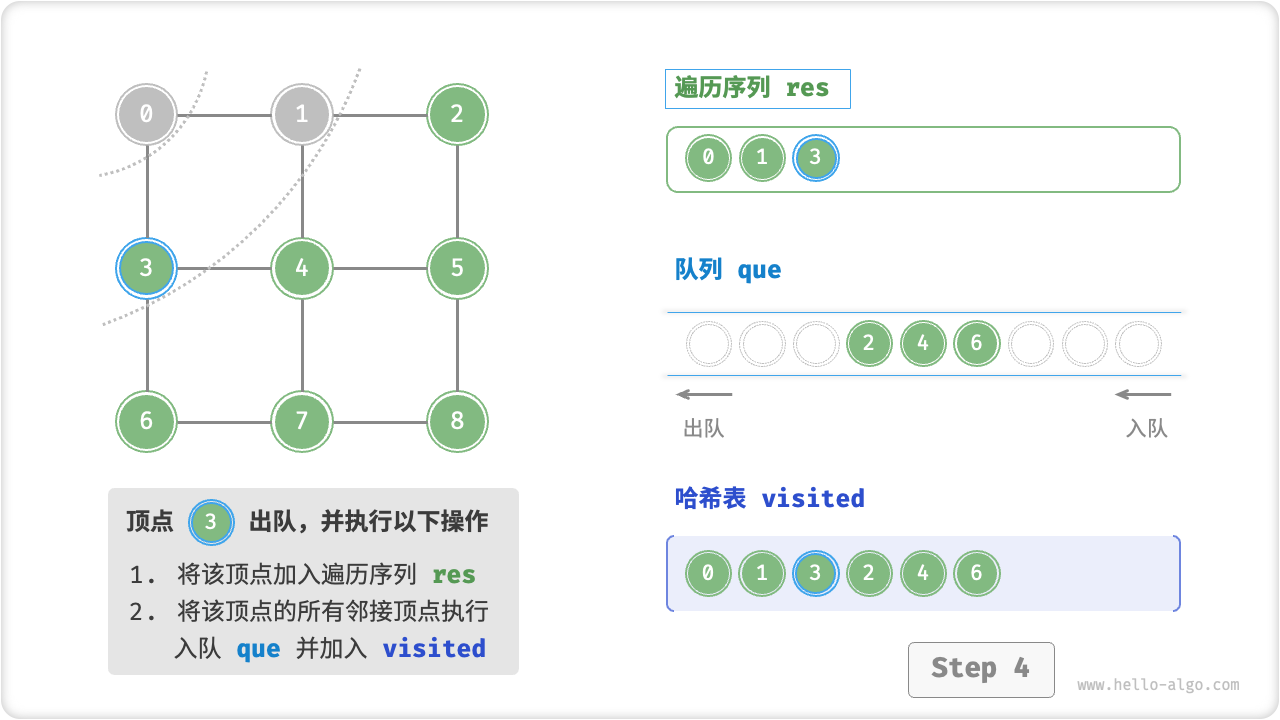
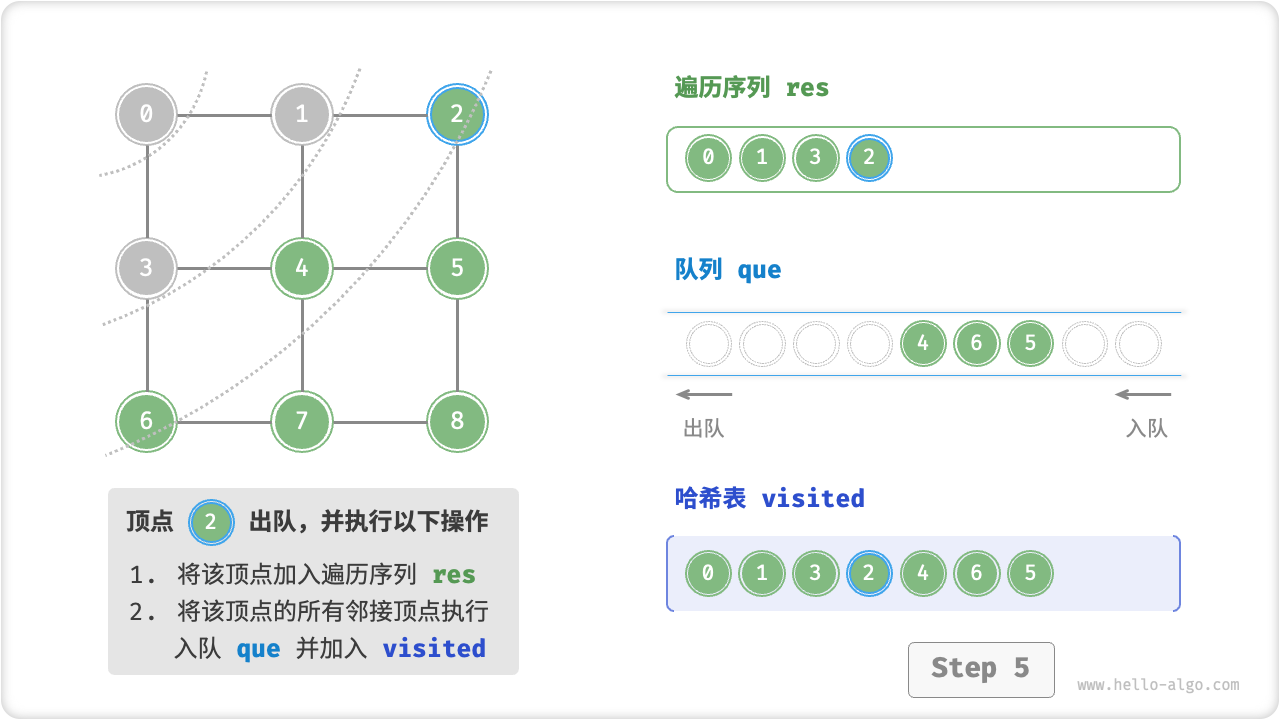
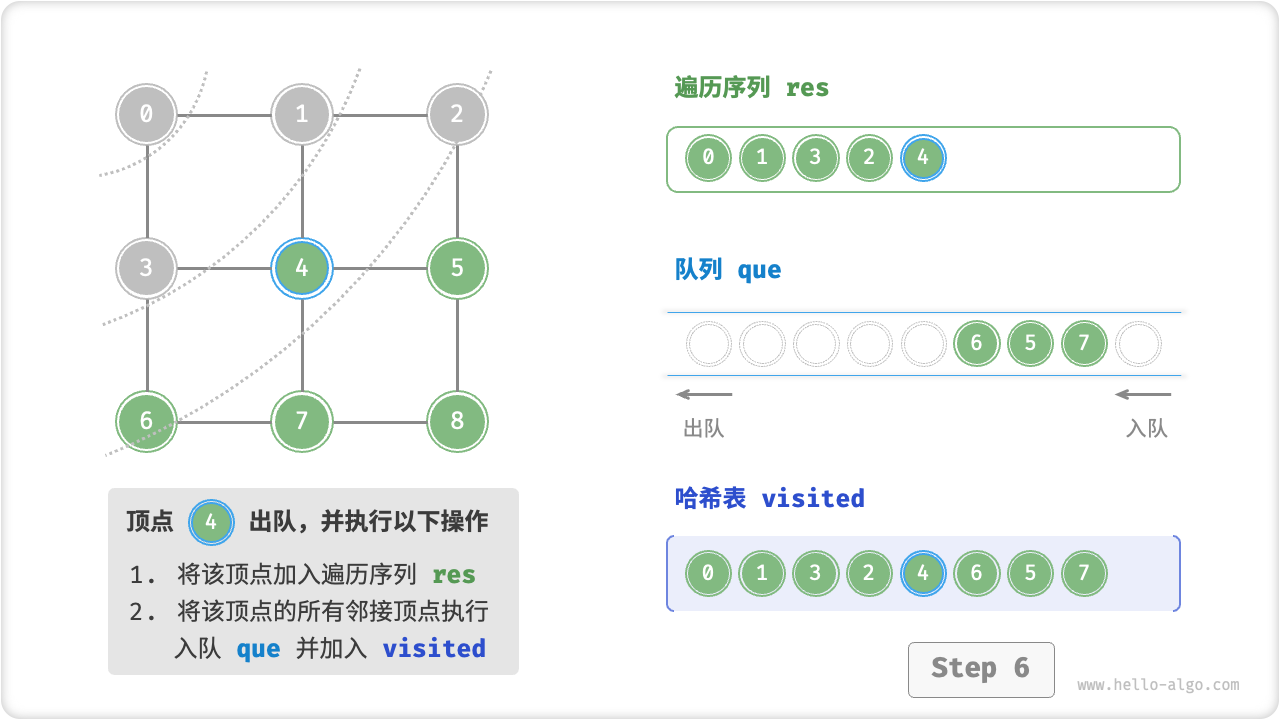
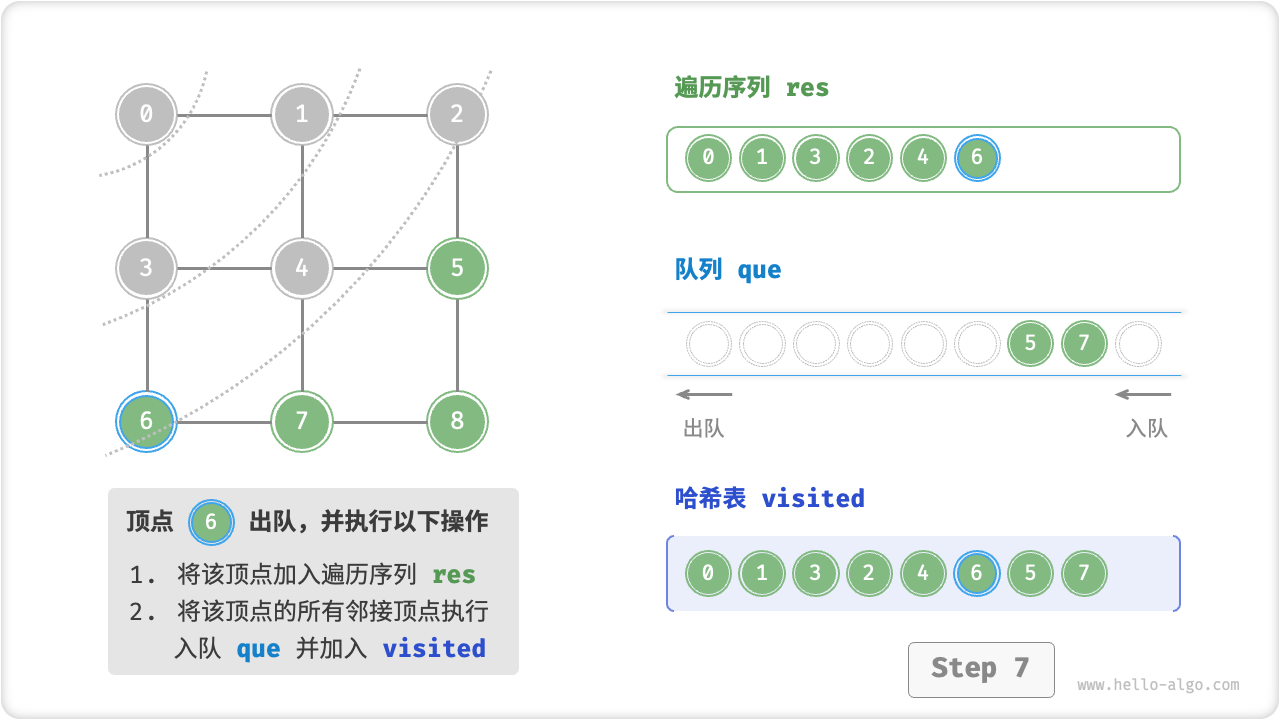
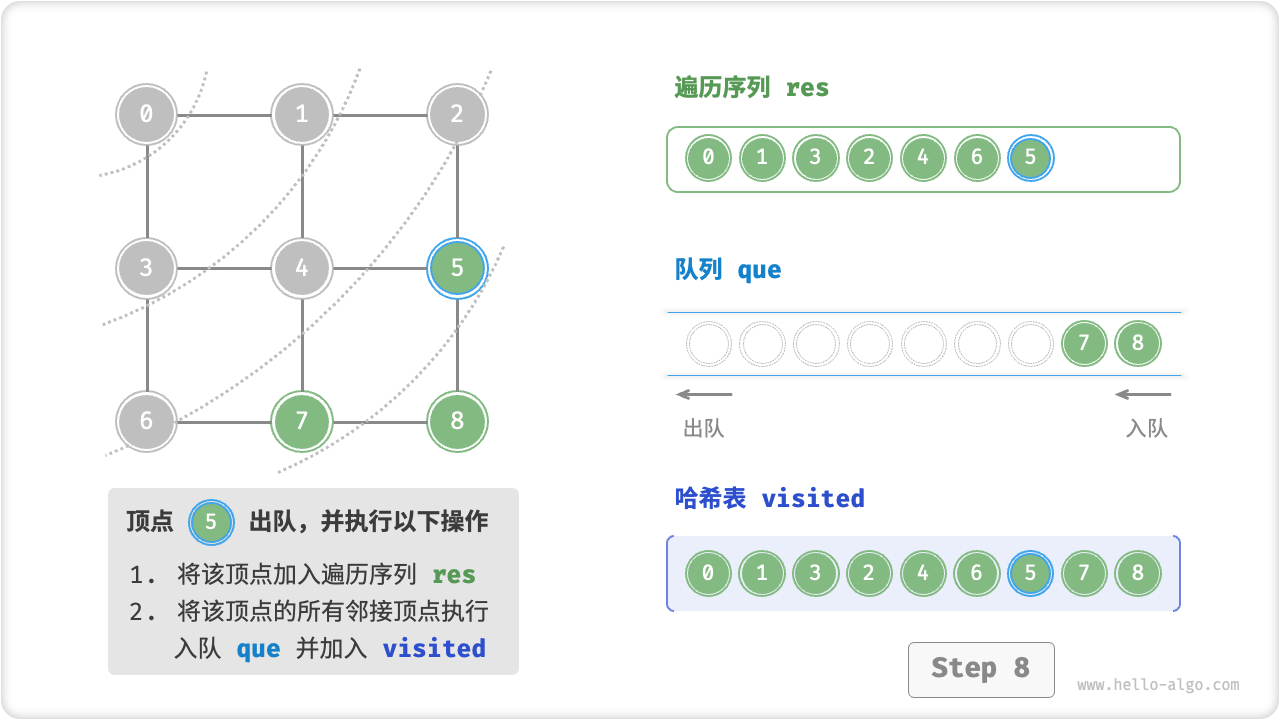
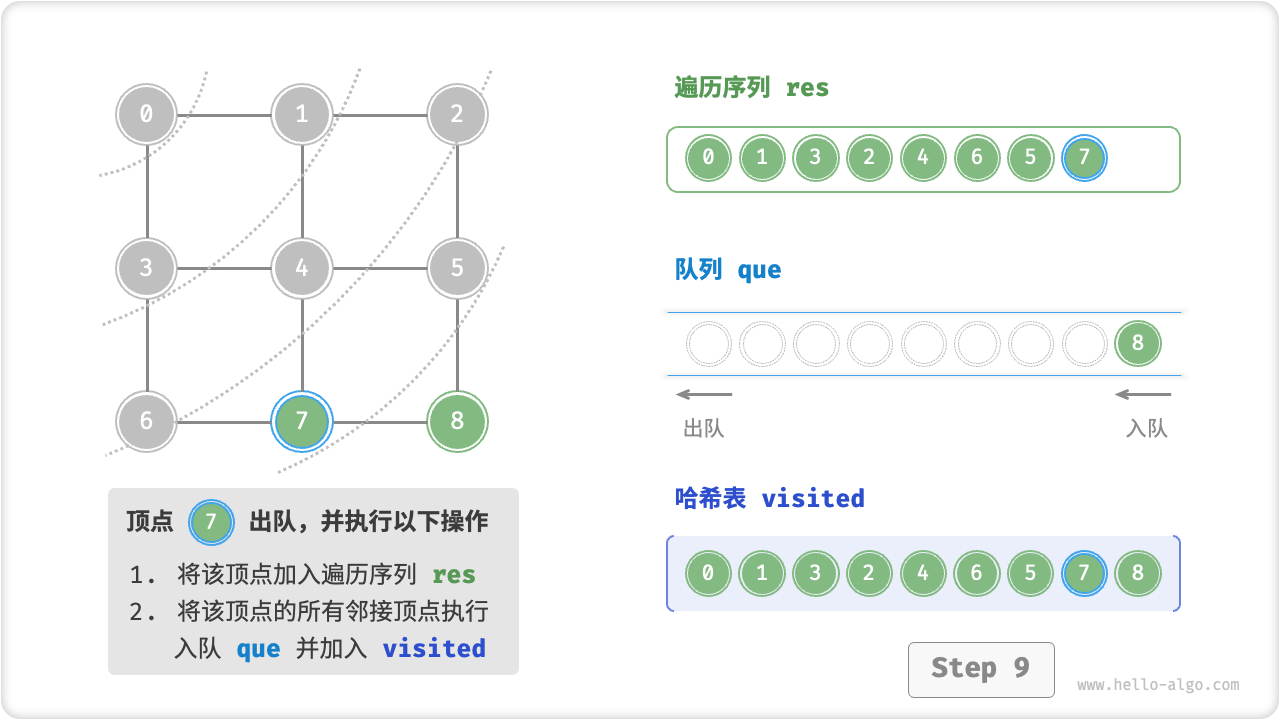
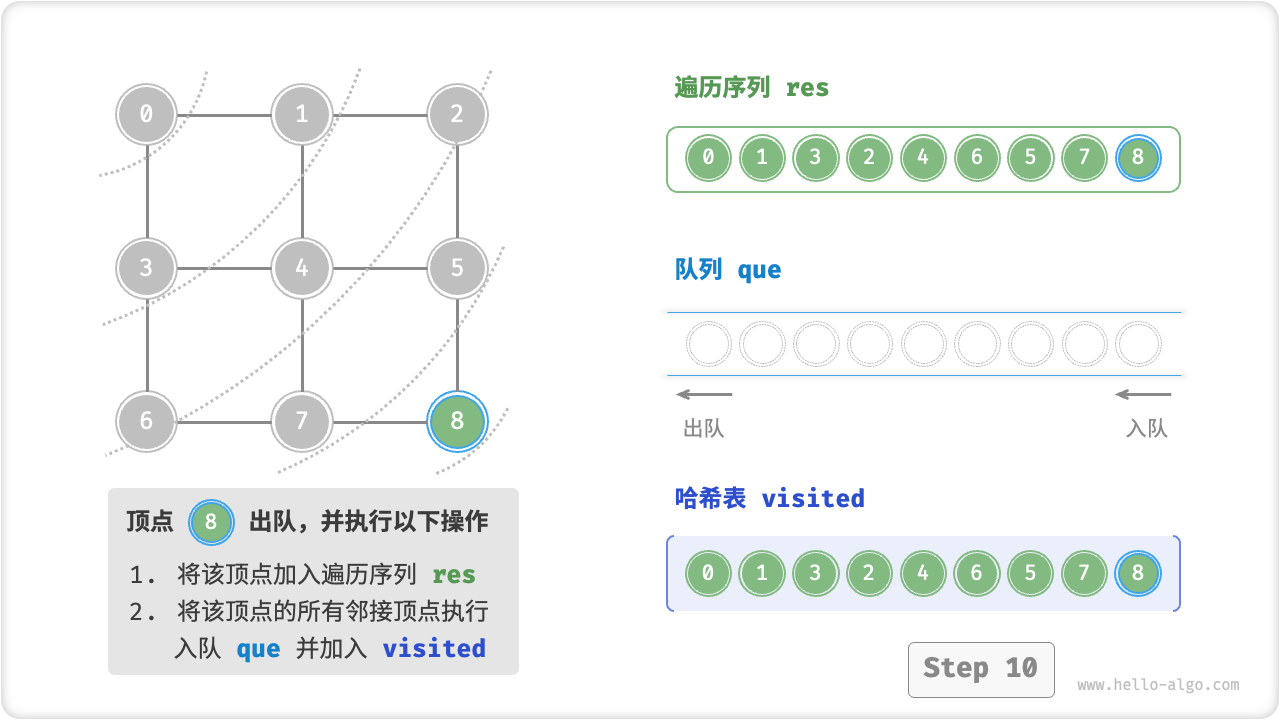
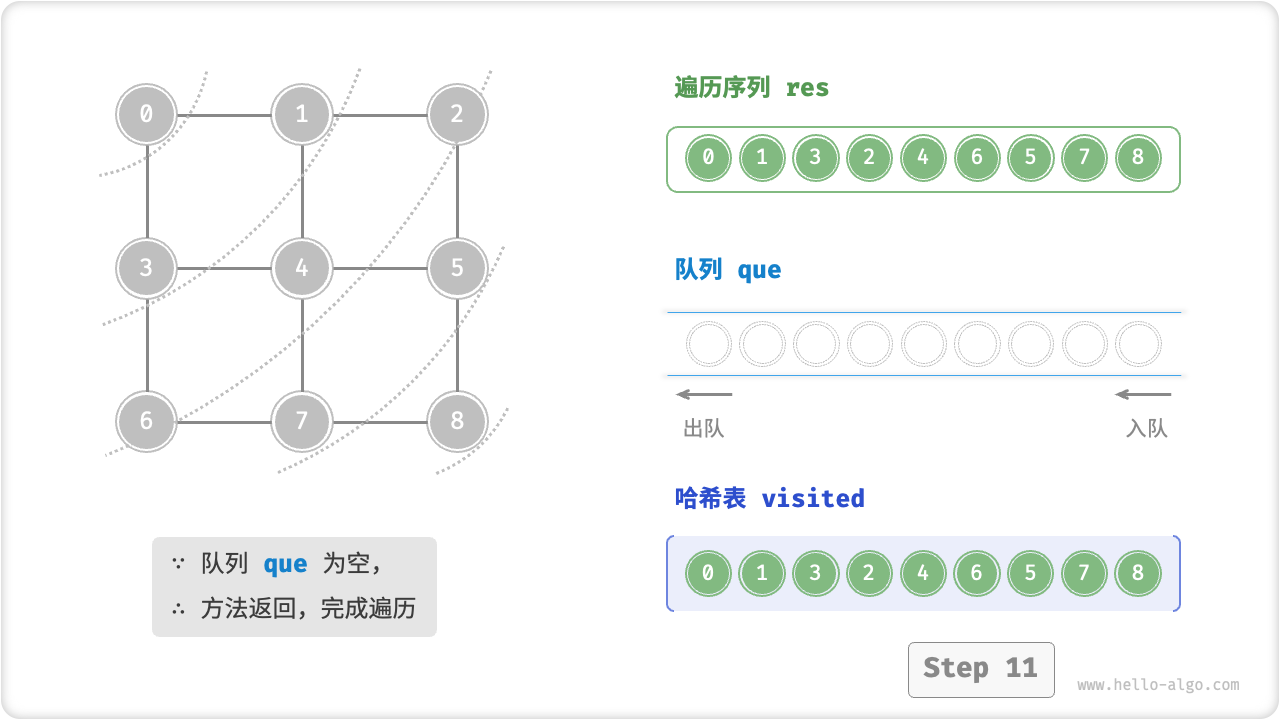
广度优先遍历是一种由近及远的遍历方式，从距离最近的顶点开始访问，并一层层向外扩张。具体来说，从某个顶点出发，先遍历该顶点的所有邻接顶点，然后遍历下一个顶点的所有邻接顶点，以此类推，直至所有顶点访问完毕。

算法实现

BFS 通常借助「队列」来实现。队列具有“先入先出”的性质，这与 BFS 的“由近及远”的思想异曲同工。

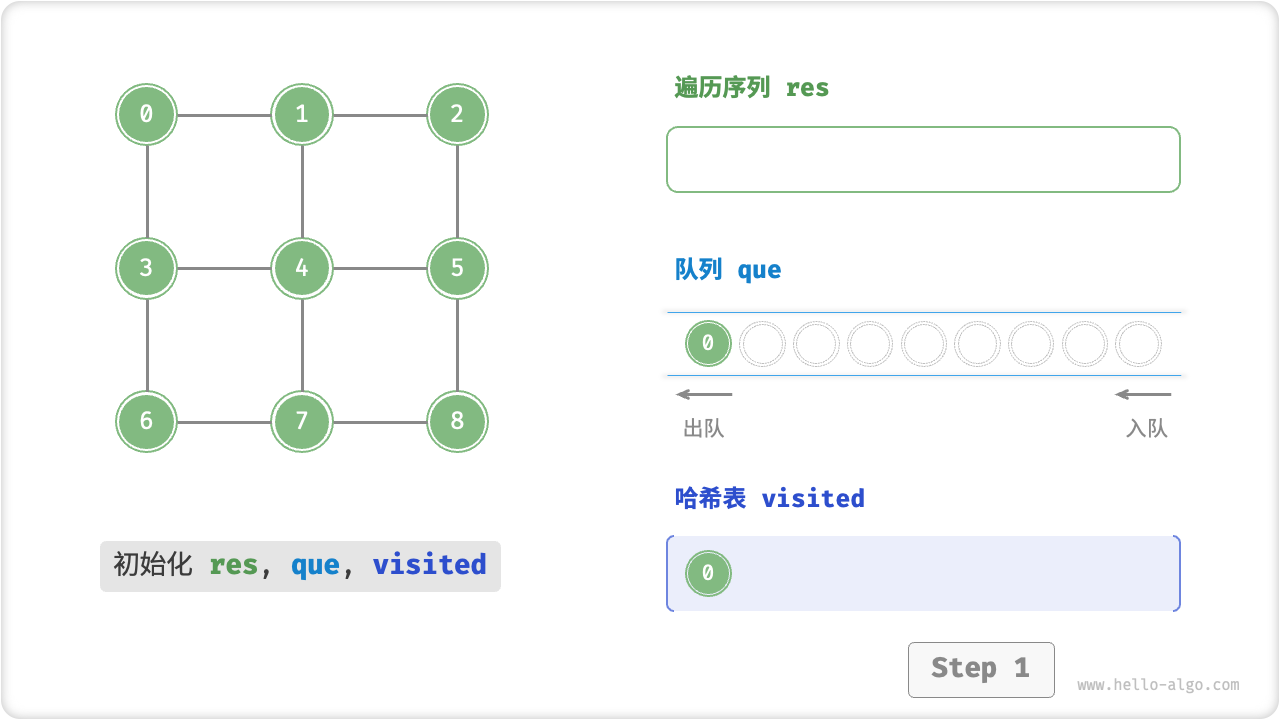
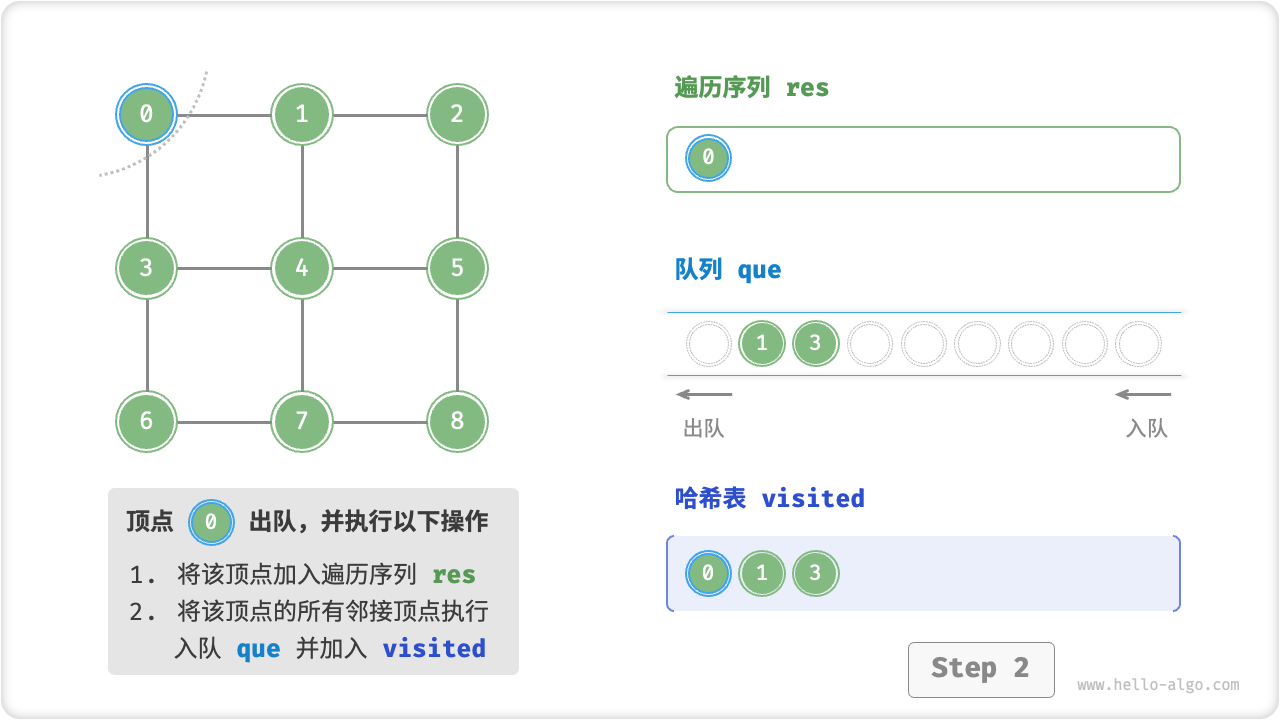
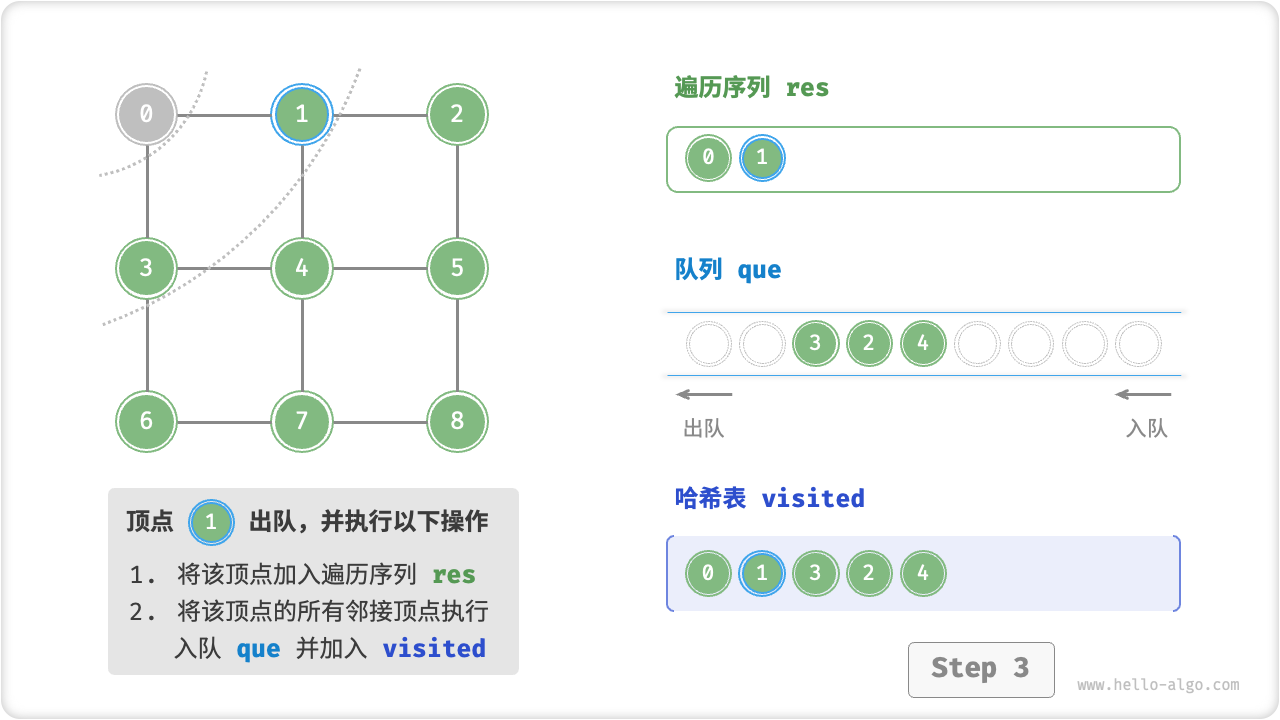
1. 将遍历起始顶点 startVet 加入队列，并开启循环；
2. 在循环的每轮迭代中，弹出队首顶点并记录访问，然后将该顶点的所有邻接顶点加入到队列尾部；
3. 循环步骤 2. ，直到所有顶点被访问完成后结束；

为了防止重复遍历顶点，我们需要借助一个哈希表 visited 来记录哪些节点已被访问。

=== "Java"

```java title="graph_bfs.java"
[class]{graph_bfs}-[func]{graphBFS}
```

=== "C++"

```cpp title="graph_bfs.cpp"
[class]{}-[func]{graphBFS}
```

=== "Python"

```python title="graph_bfs.py"
[class]{}-[func]{graph_bfs}
```

=== "Go"

```go title="graph_bfs.go"
[class]{}-[func]{graphBFS}
```

=== "JavaScript"

```javascript title="graph_bfs.js"
[class]{}-[func]{graphBFS}
```

=== "TypeScript"

```typescript title="graph_bfs.ts"
[class]{}-[func]{graphBFS}
```

=== "C"

```c title="graph_bfs.c"
[class]{}-[func]{graphBFS}
```

=== "C#"

```csharp title="graph_bfs.cs"
[class]{graph_bfs}-[func]{graphBFS}
```

=== "Swift"

```swift title="graph_bfs.swift"
[class]{}-[func]{graphBFS}
```

=== "Zig"

```zig title="graph_bfs.zig"
[class]{}-[func]{graphBFS}
```

代码相对抽象，建议对照以下动画图示来加深理解。

=== "<1>"

=== "<2>"

=== "<3>"

=== "<4>"

=== "<5>"

=== "<6>"

=== "<7>"

=== "<8>"

=== "<9>"

=== "<10>"

=== "<11>"

!!! question "广度优先遍历的序列是否唯一？"

不唯一。广度优先遍历只要求按“由近及远”的顺序遍历，**而多个相同距离的顶点的遍历顺序是允许被任意打乱的**。以上图为例，顶点 $1$ , $3$ 的访问顺序可以交换、顶点 $2$ , $4$ , $6$ 的访问顺序也可以任意交换。

复杂度分析

时间复杂度： 所有顶点都会入队并出队一次，使用 O(|V|) 时间；在遍历邻接顶点的过程中，由于是无向图，因此所有边都会被访问 2 次，使用 O(2|E|) 时间；总体使用 O(|V| + |E|) 时间。

空间复杂度： 列表 res ，哈希表 visited ，队列 que 中的顶点数量最多为 |V| ，使用 O(|V|) 空间。

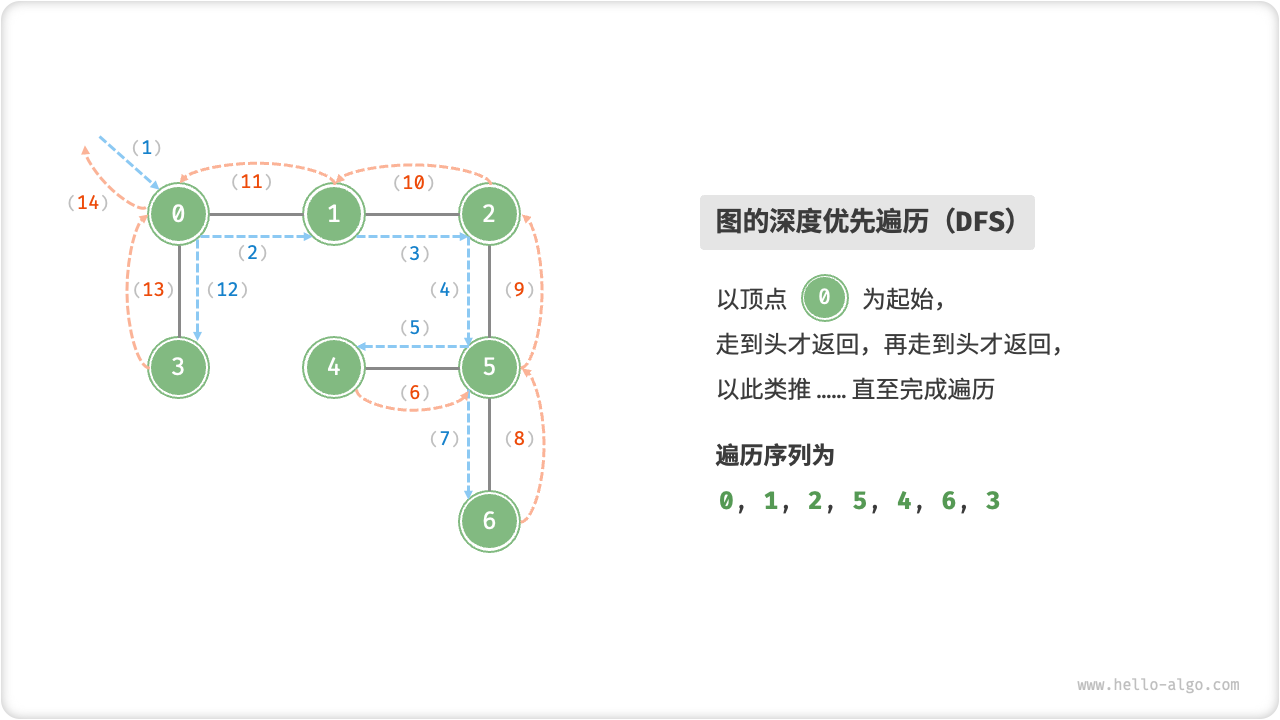
深度优先遍历

深度优先遍历是一种优先走到底、无路可走再回头的遍历方式。具体地，从某个顶点出发，访问当前顶点的某个邻接顶点，直到走到尽头时返回，再继续走到尽头并返回，以此类推，直至所有顶点遍历完成。

算法实现

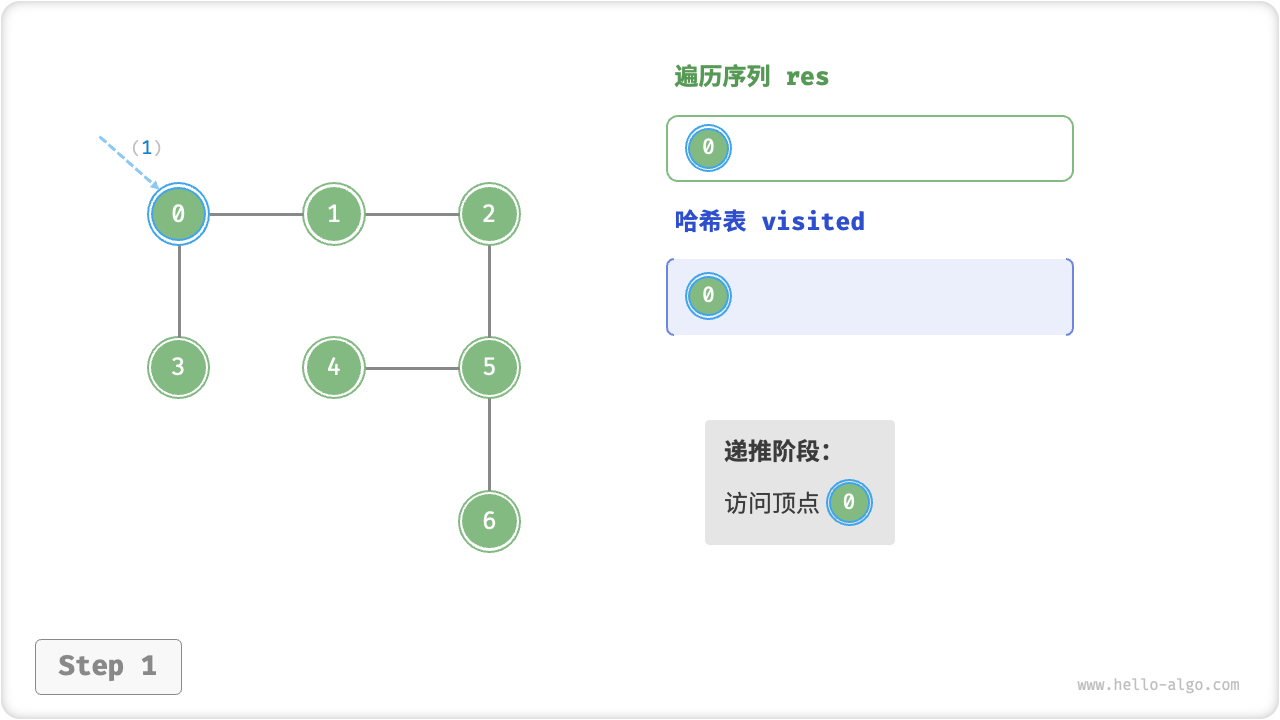
这种“走到尽头 + 回溯”的算法形式通常基于递归来实现。与 BFS 类似，在 DFS 中我们也需要借助一个哈希表 visited 来记录已被访问的顶点，以避免重复访问顶点。

=== "Java"

```java title="graph_dfs.java"
[class]{graph_dfs}-[func]{dfs}

[class]{graph_dfs}-[func]{graphDFS}
```

=== "C++"

```cpp title="graph_dfs.cpp"
[class]{}-[func]{dfs}

[class]{}-[func]{graphDFS}
```

=== "Python"

```python title="graph_dfs.py"
[class]{}-[func]{dfs}

[class]{}-[func]{graph_dfs}
```

=== "Go"

```go title="graph_dfs.go"
[class]{}-[func]{dfs}

[class]{}-[func]{graphDFS}
```

=== "JavaScript"

```javascript title="graph_dfs.js"
[class]{}-[func]{dfs}

[class]{}-[func]{graphDFS}
```

=== "TypeScript"

```typescript title="graph_dfs.ts"
[class]{}-[func]{dfs}

[class]{}-[func]{graphDFS}
```

=== "C"

```c title="graph_dfs.c"
[class]{}-[func]{dfs}

[class]{}-[func]{graphDFS}
```

=== "C#"

```csharp title="graph_dfs.cs"
[class]{graph_dfs}-[func]{dfs}

[class]{graph_dfs}-[func]{graphDFS}
```

=== "Swift"

```swift title="graph_dfs.swift"
[class]{}-[func]{dfs}

[class]{}-[func]{graphDFS}
```

=== "Zig"

```zig title="graph_dfs.zig"
[class]{}-[func]{dfs}

[class]{}-[func]{graphDFS}
```

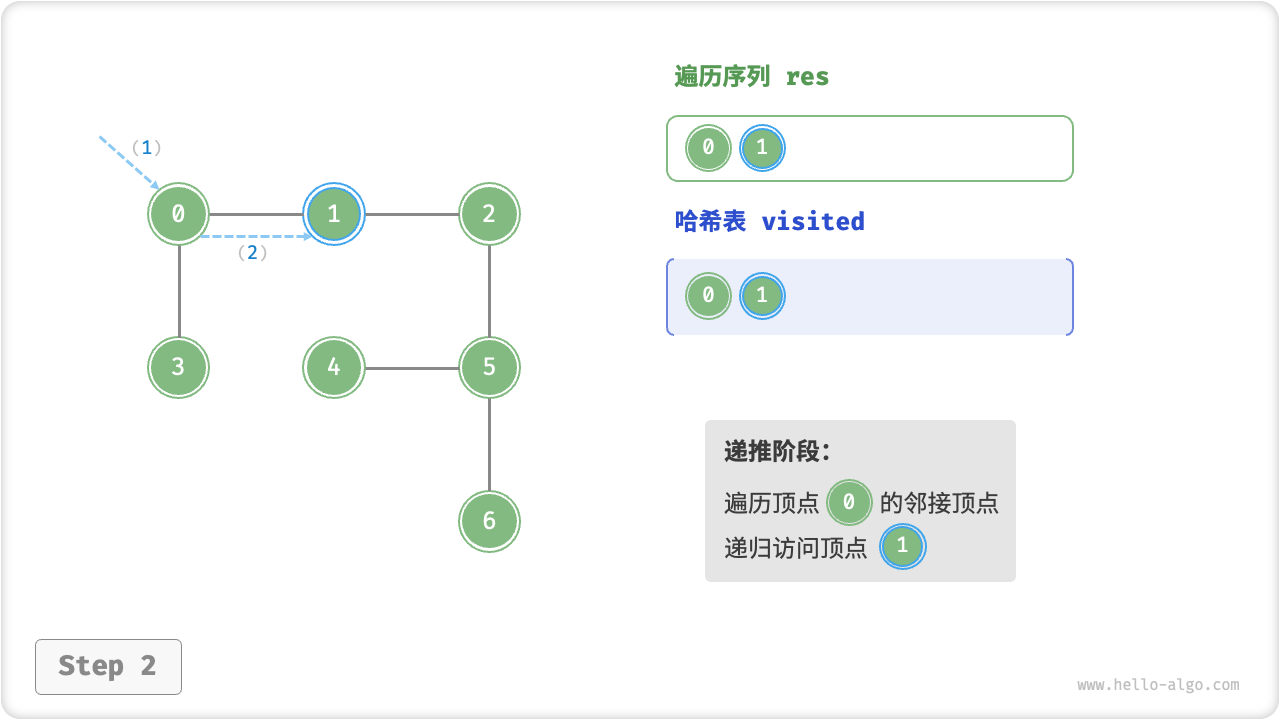
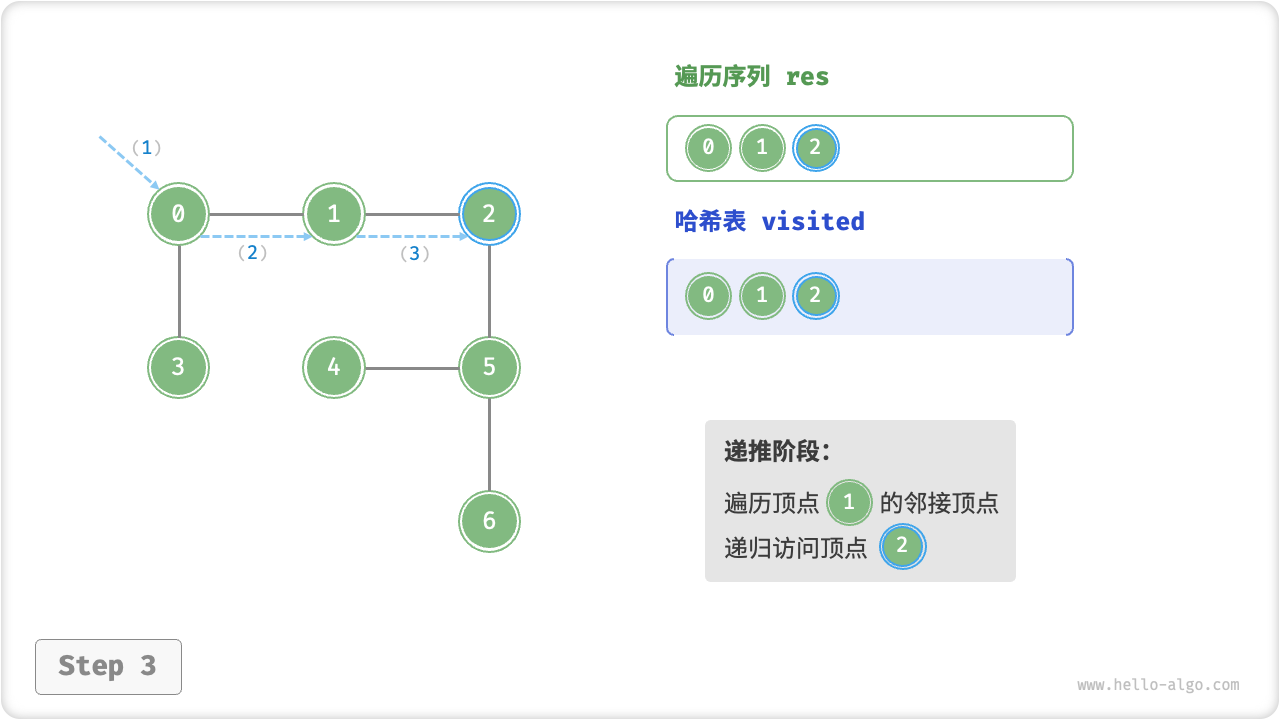
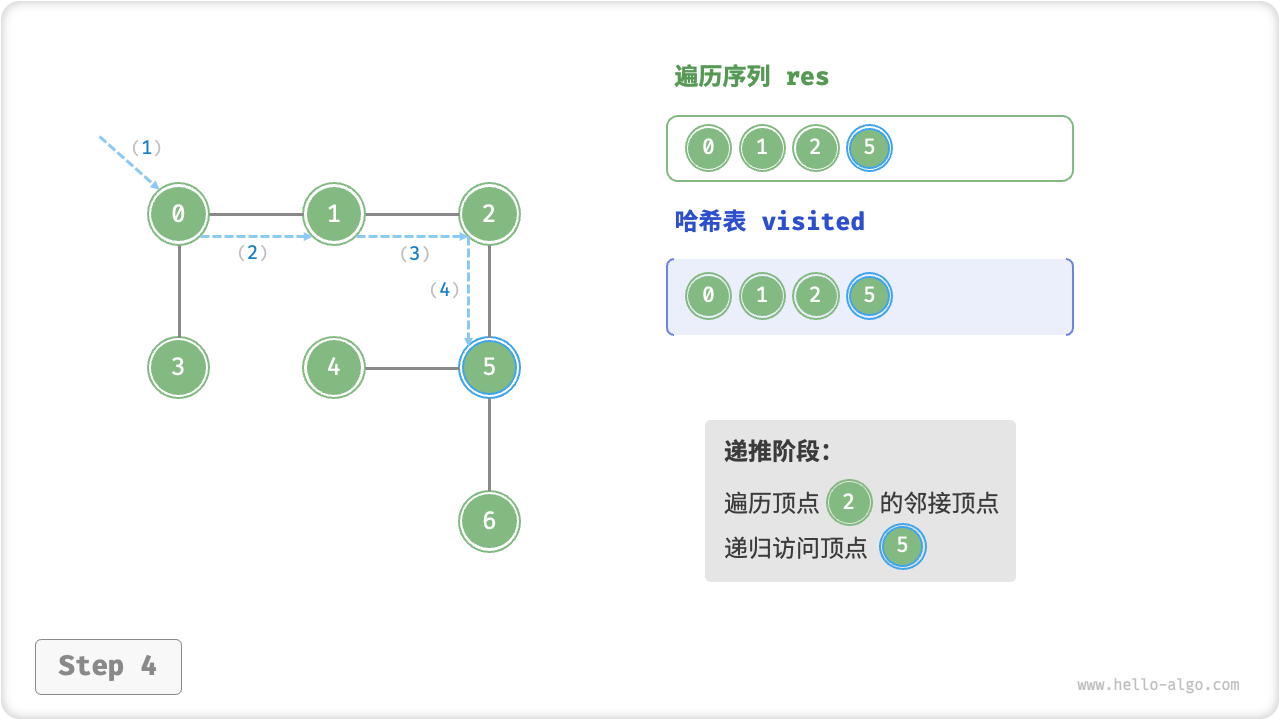
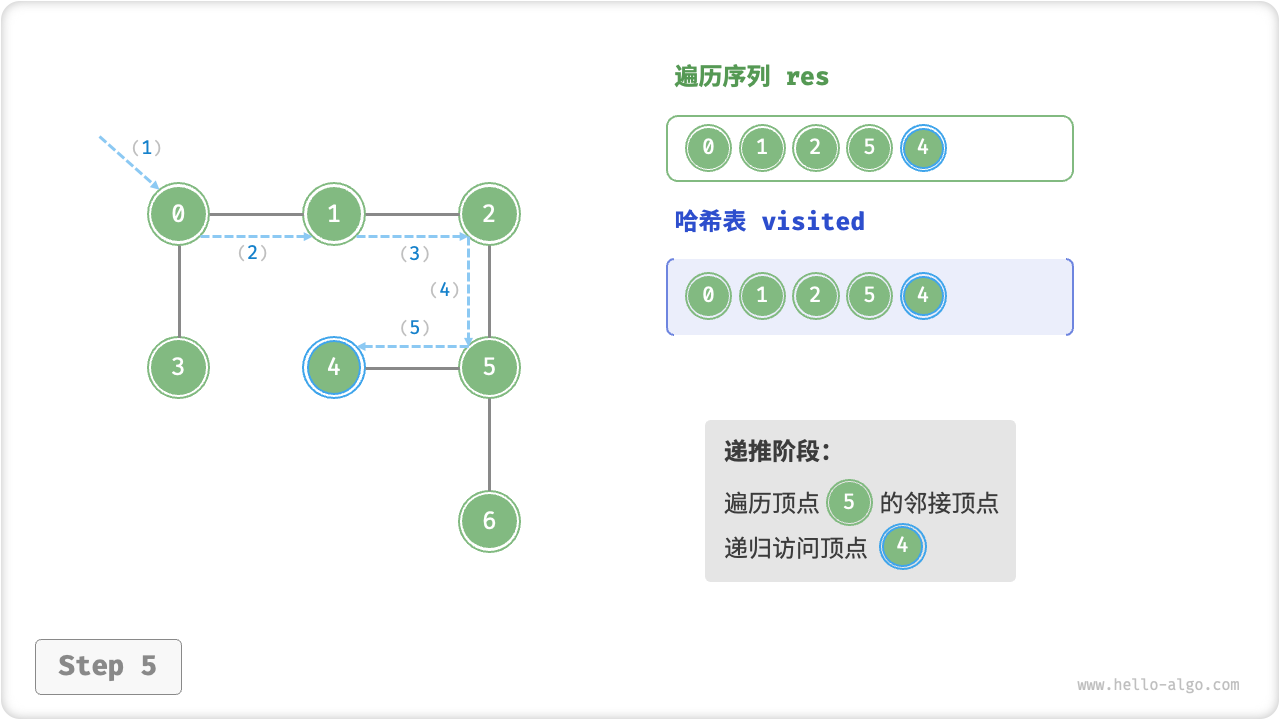
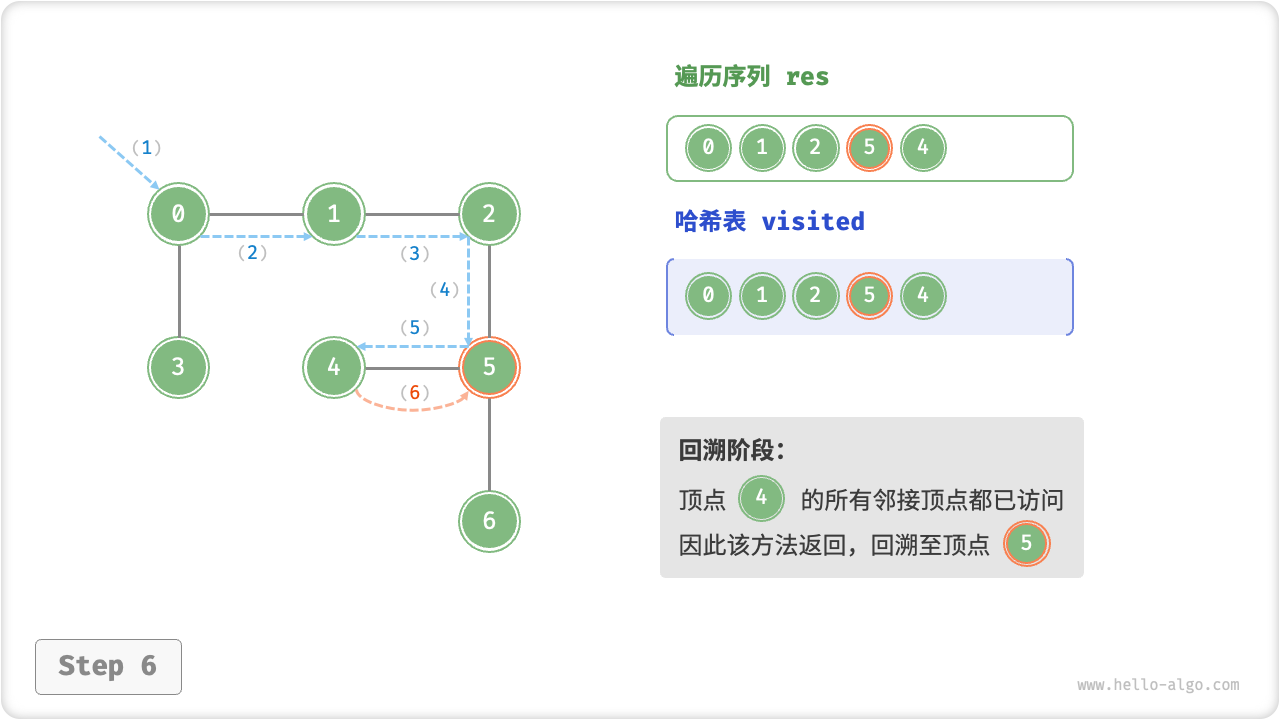
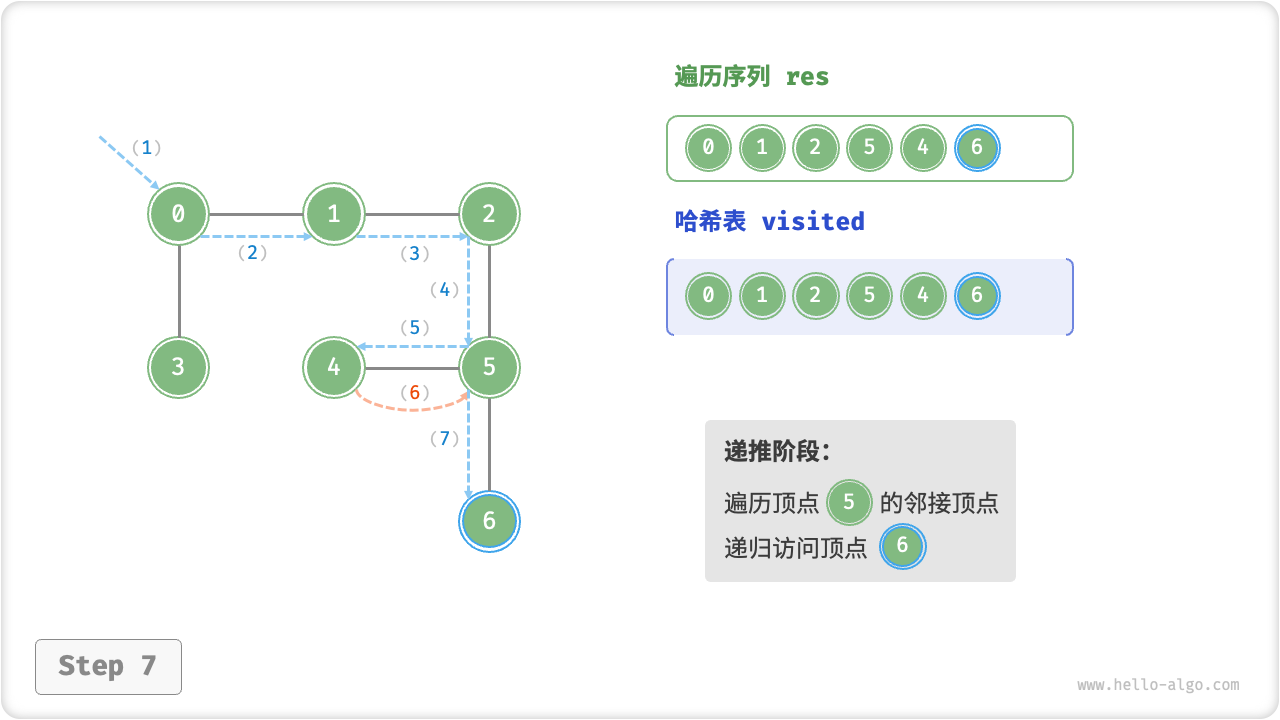
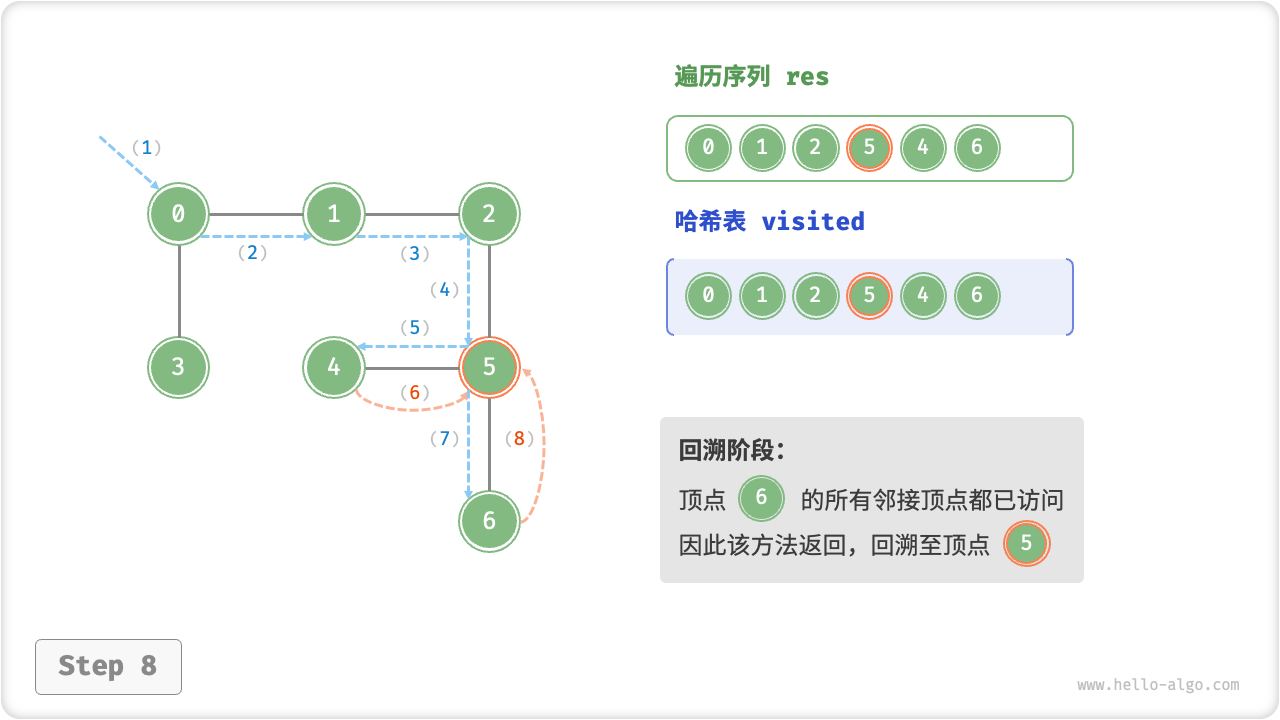
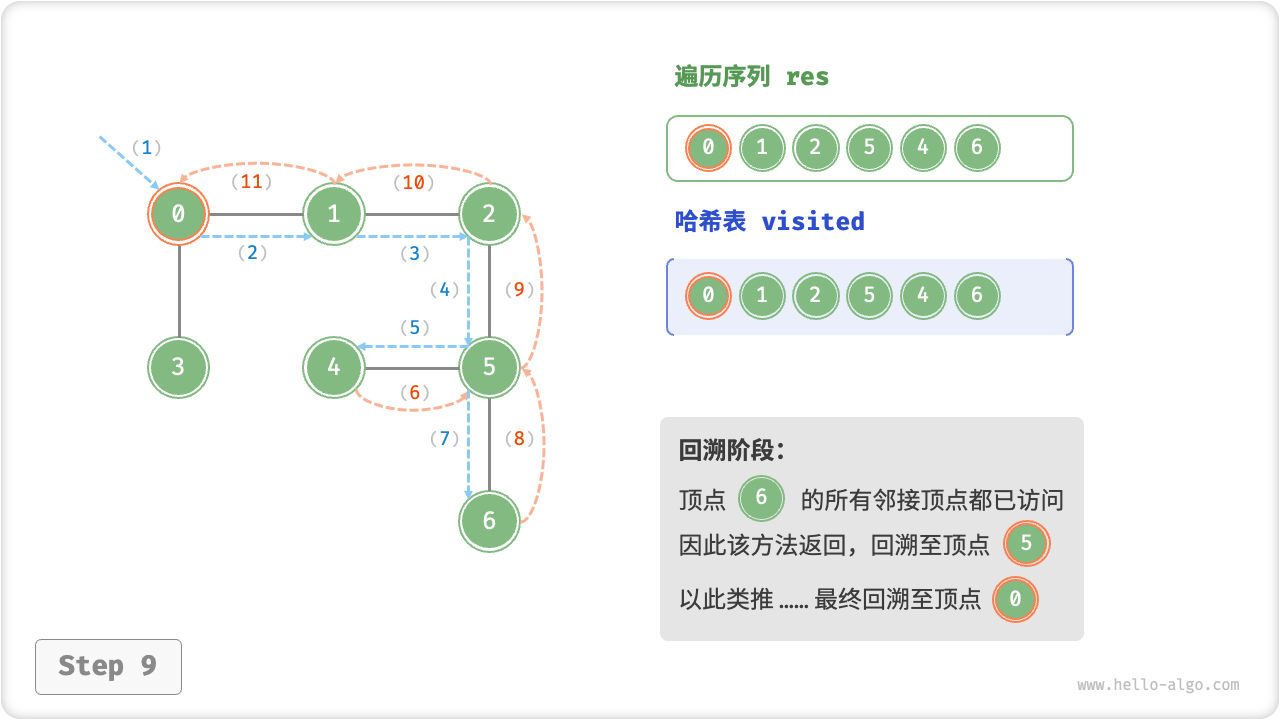
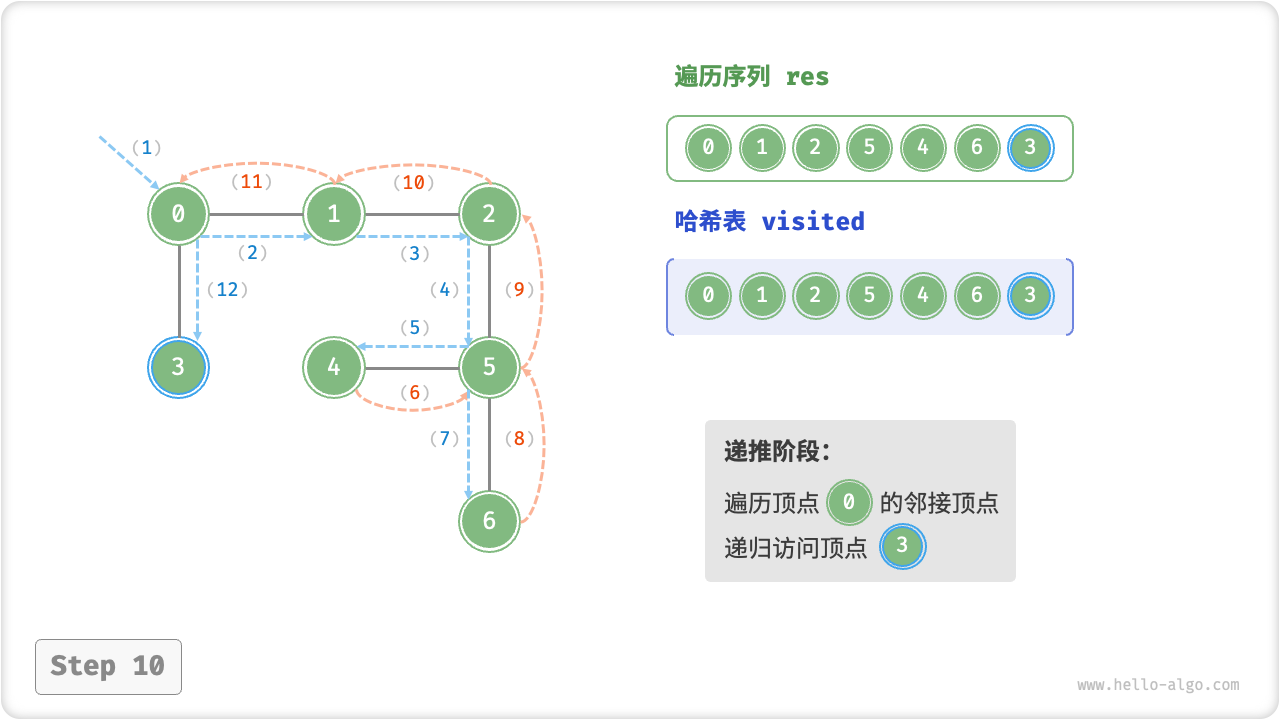
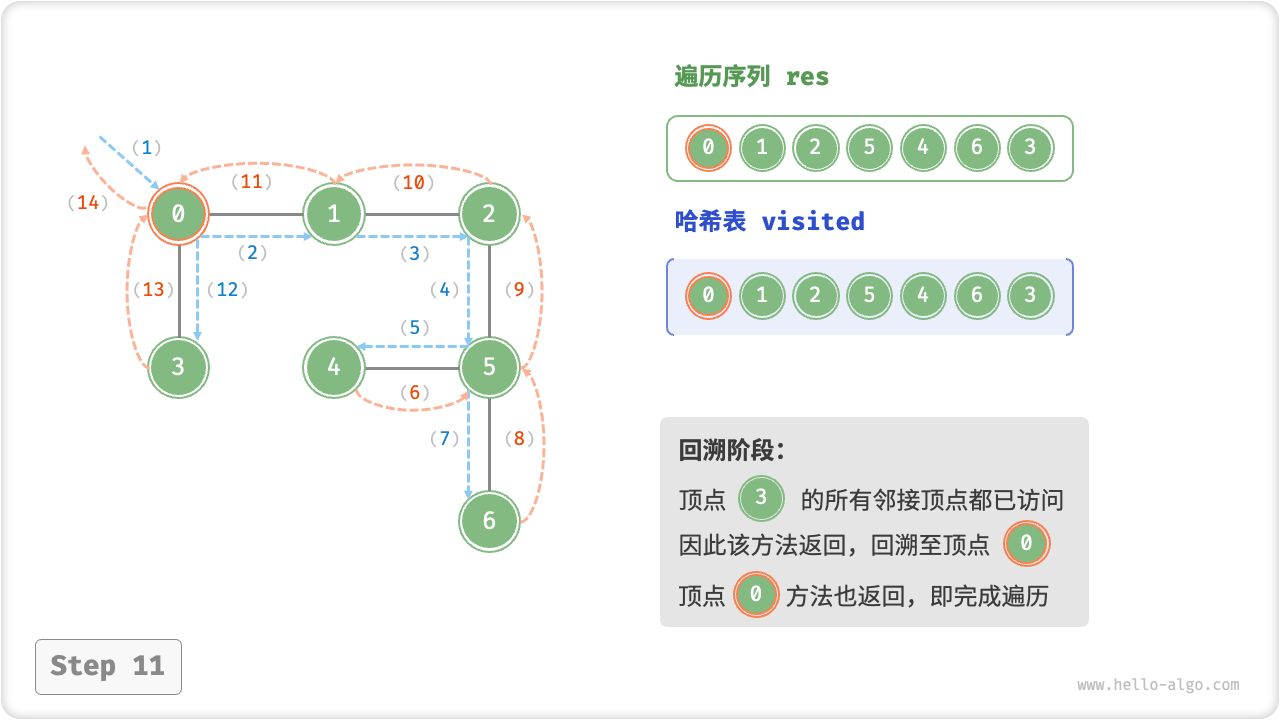
深度优先遍历的算法流程如下图所示，其中：

• 直虚线代表向下递推，表示开启了一个新的递归方法来访问新顶点；
• 曲虚线代表向上回溯，表示此递归方法已经返回，回溯到了开启此递归方法的位置；

为了加深理解，建议将图示与代码结合起来，在脑中（或者用笔画下来）模拟整个 DFS 过程，包括每个递归方法何时开启、何时返回。

=== "<1>"

=== "<2>"

=== "<3>"

=== "<4>"

=== "<5>"

=== "<6>"

=== "<7>"

=== "<8>"

=== "<9>"

=== "<10>"

=== "<11>"

!!! question "深度优先遍历的序列是否唯一？"

与广度优先遍历类似，深度优先遍历序列的顺序也不是唯一的。给定某顶点，先往哪个方向探索都可以，即邻接顶点的顺序可以任意打乱，都是深度优先遍历。

以树的遍历为例，“根 $\rightarrow$ 左 $\rightarrow$ 右”、“左 $\rightarrow$ 根 $\rightarrow$ 右”、“左 $\rightarrow$ 右 $\rightarrow$ 根”分别对应前序、中序、后序遍历，它们展示了三种不同的遍历优先级，然而这三者都属于深度优先遍历。

复杂度分析

时间复杂度： 所有顶点都会被访问 1 次，使用 O(|V|) 时间；所有边都会被访问 2 次，使用 O(2|E|) 时间；总体使用 O(|V| + |E|) 时间。

空间复杂度： 列表 res ，哈希表 visited 顶点数量最多为 |V| ，递归深度最大为 |V| ，因此使用 O(|V|) 空间。