hello-algo/zh-hant/docs/chapter_heap/top_k.md

Top-k 問題

!!! question

給定一個長度為 $n$ 的無序陣列 `nums` ，請返回陣列中最大的 $k$ 個元素。

對於該問題，我們先介紹兩種思路比較直接的解法，再介紹效率更高的堆積解法。

方法一：走訪選擇

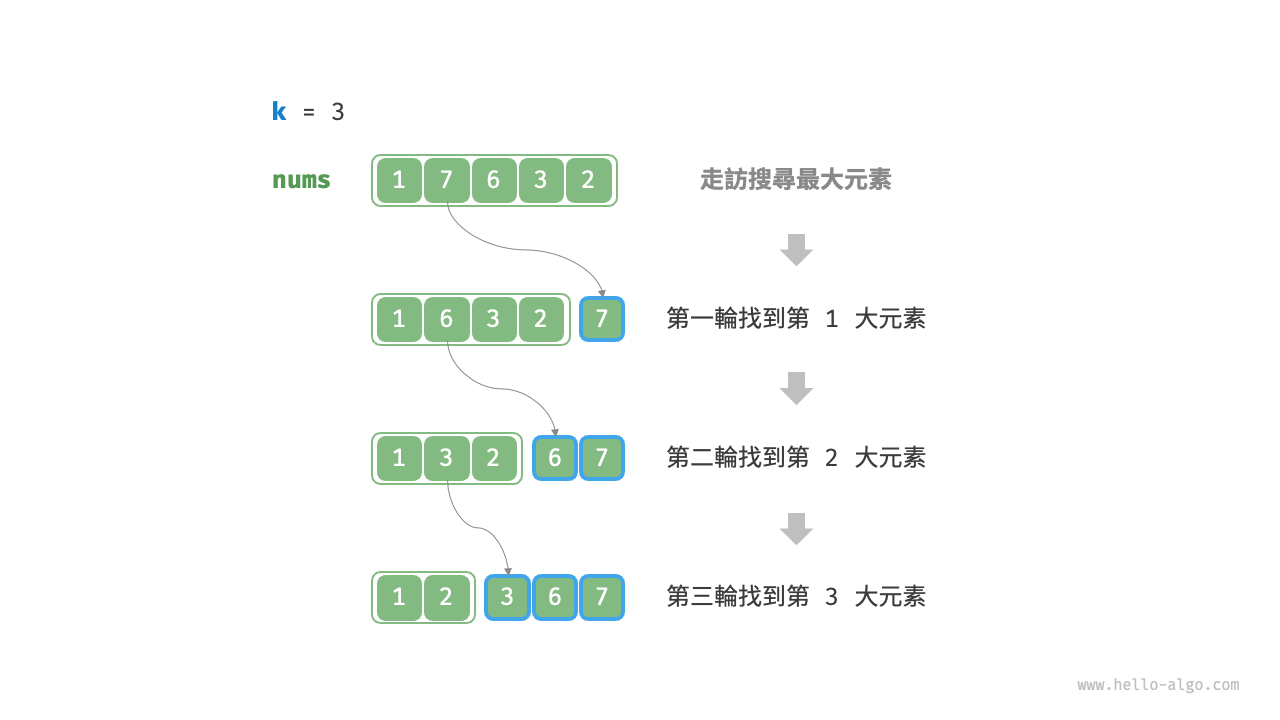
我們可以進行下圖所示的 k 輪走訪，分別在每輪中提取第 $1$、$2$、$\dots$、k 大的元素，時間複雜度為 O(nk) 。

此方法只適用於 k \ll n 的情況，因為當 k 與 n 比較接近時，其時間複雜度趨向於 O(n^2) ，非常耗時。

!!! tip

當 $k = n$ 時，我們可以得到完整的有序序列，此時等價於“選擇排序”演算法。

方法二：排序

如下圖所示，我們可以先對陣列 nums 進行排序，再返回最右邊的 k 個元素，時間複雜度為 O(n \log n) 。

顯然，該方法“超額”完成任務了，因為我們只需找出最大的 k 個元素即可，而不需要排序其他元素。

方法三：堆積

我們可以基於堆積更加高效地解決 Top-k 問題，流程如下圖所示。

1. 初始化一個小頂堆積，其堆積頂元素最小。
2. 先將陣列的前 k 個元素依次入堆積。
3. 從第 k + 1 個元素開始，若當前元素大於堆積頂元素，則將堆積頂元素出堆積，並將當前元素入堆積。
4. 走訪完成後，堆積中儲存的就是最大的 k 個元素。

=== "<1>"

=== "<2>"

=== "<3>"

=== "<4>"

=== "<5>"

=== "<6>"

=== "<7>"

=== "<8>"

=== "<9>"

示例程式碼如下：

[file]{top_k}-[class]{}-[func]{top_k_heap}

總共執行了 n 輪入堆積和出堆積，堆積的最大長度為 k ，因此時間複雜度為 O(n \log k) 。該方法的效率很高，當 k 較小時，時間複雜度趨向 O(n) ；當 k 較大時，時間複雜度不會超過 O(n \log n) 。

另外，該方法適用於動態資料流的使用場景。在不斷加入資料時，我們可以持續維護堆積內的元素，從而實現最大的 k 個元素的動態更新。