hello-algo/zh-hant/docs/chapter_dynamic_programming/knapsack_problem.md

0-1 背包問題

背包問題是一個非常好的動態規劃入門題目，是動態規劃中最常見的問題形式。其具有很多變種，例如 0-1 背包問題、完全背包問題、多重背包問題等。

在本節中，我們先來求解最常見的 0-1 背包問題。

!!! question

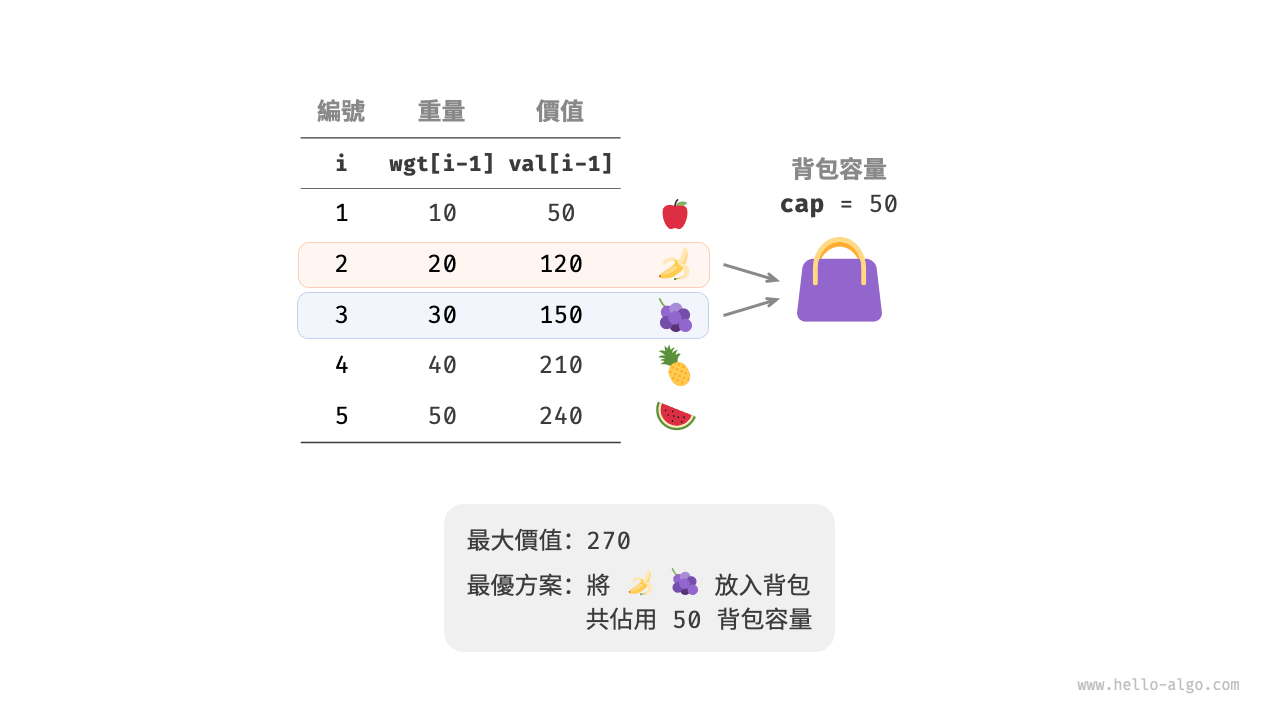
給定 $n$ 個物品，第 $i$ 個物品的重量為 $wgt[i-1]$、價值為 $val[i-1]$ ，和一個容量為 $cap$ 的背包。每個物品只能選擇一次，問在限定背包容量下能放入物品的最大價值。

觀察下圖，由於物品編號 i 從 1 開始計數，陣列索引從 0 開始計數，因此物品 i 對應重量 wgt[i-1] 和價值 val[i-1] 。

我們可以將 0-1 背包問題看作一個由 n 輪決策組成的過程，對於每個物體都有不放入和放入兩種決策，因此該問題滿足決策樹模型。

該問題的目標是求解“在限定背包容量下能放入物品的最大價值”，因此較大機率是一個動態規劃問題。

第一步：思考每輪的決策，定義狀態，從而得到 dp 表

對於每個物品來說，不放入背包，背包容量不變；放入背包，背包容量減小。由此可得狀態定義：當前物品編號 i 和背包容量 c ，記為 [i, c] 。

狀態 [i, c] 對應的子問題為：前 i 個物品在容量為 c 的背包中的最大價值，記為 dp[i, c] 。

待求解的是 dp[n, cap] ，因此需要一個尺寸為 (n+1) \times (cap+1) 的二維 dp 表。

第二步：找出最優子結構，進而推導出狀態轉移方程

當我們做出物品 i 的決策後，剩餘的是前 i-1 個物品決策的子問題，可分為以下兩種情況。

• 不放入物品 $i$ ：背包容量不變，狀態變化為 [i-1, c] 。
• 放入物品 $i$ ：背包容量減少 wgt[i-1] ，價值增加 val[i-1] ，狀態變化為 [i-1, c-wgt[i-1]] 。

上述分析向我們揭示了本題的最優子結構：最大價值 dp[i, c] 等於不放入物品 i 和放入物品 i 兩種方案中價值更大的那一個。由此可推導出狀態轉移方程：

$$ dp[i, c] = \max(dp[i-1, c], dp[i-1, c - wgt[i-1]] + val[i-1])

需要注意的是，若當前物品重量 wgt[i - 1] 超出剩餘背包容量 c ，則只能選擇不放入背包。

第三步：確定邊界條件和狀態轉移順序

當無物品或背包容量為 0 時最大價值為 0 ，即首列 dp[i, 0] 和首行 dp[0, c] 都等於 0 。

當前狀態 [i, c] 從上方的狀態 [i-1, c] 和左上方的狀態 [i-1, c-wgt[i-1]] 轉移而來，因此透過兩層迴圈正序走訪整個 dp 表即可。

根據以上分析，我們接下來按順序實現暴力搜尋、記憶化搜尋、動態規劃解法。

方法一：暴力搜尋

搜尋程式碼包含以下要素。

• 遞迴參數：狀態 [i, c] 。
• 返回值：子問題的解 dp[i, c] 。
• 終止條件：當物品編號越界 i = 0 或背包剩餘容量為 0 時，終止遞迴並返回價值 0 。
• 剪枝：若當前物品重量超出背包剩餘容量，則只能選擇不放入背包。

[file]{knapsack}-[class]{}-[func]{knapsack_dfs}

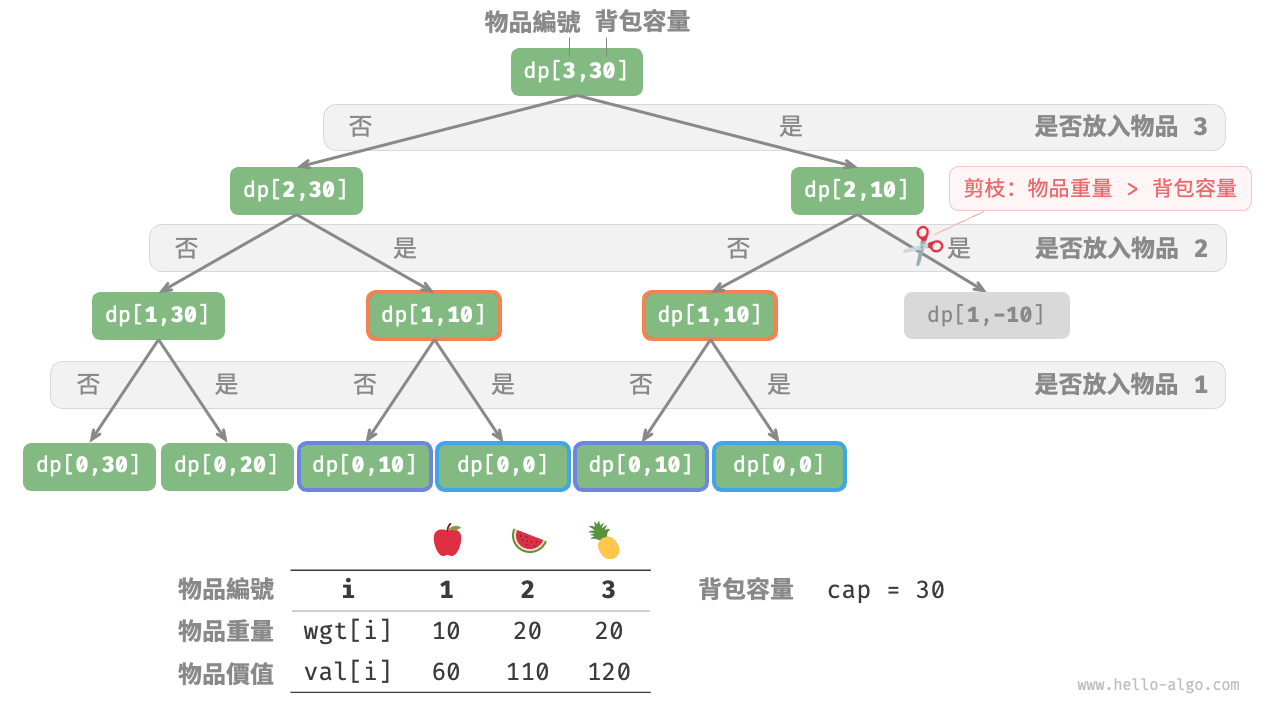
如下圖所示，由於每個物品都會產生不選和選兩條搜尋分支，因此時間複雜度為 O(2^n) 。

觀察遞迴樹，容易發現其中存在重疊子問題，例如 dp[1, 10] 等。而當物品較多、背包容量較大，尤其是相同重量的物品較多時，重疊子問題的數量將會大幅增多。

方法二：記憶化搜尋

為了保證重疊子問題只被計算一次，我們藉助記憶串列 mem 來記錄子問題的解，其中 mem[i][c] 對應 dp[i, c] 。

引入記憶化之後，時間複雜度取決於子問題數量，也就是 O(n \times cap) 。實現程式碼如下：

[file]{knapsack}-[class]{}-[func]{knapsack_dfs_mem}

下圖展示了在記憶化搜尋中被剪掉的搜尋分支。

方法三：動態規劃

動態規劃實質上就是在狀態轉移中填充 dp 表的過程，程式碼如下所示：

[file]{knapsack}-[class]{}-[func]{knapsack_dp}

如下圖所示，時間複雜度和空間複雜度都由陣列 dp 大小決定，即 O(n \times cap) 。

=== "<1>"

=== "<2>"

=== "<3>"

=== "<4>"

=== "<5>"

=== "<6>"

=== "<7>"

=== "<8>"

=== "<9>"

=== "<10>"

=== "<11>"

=== "<12>"

=== "<13>"

=== "<14>"

空間最佳化

由於每個狀態都只與其上一行的狀態有關，因此我們可以使用兩個陣列滾動前進，將空間複雜度從 O(n^2) 降至 O(n) 。

進一步思考，我們能否僅用一個陣列實現空間最佳化呢？觀察可知，每個狀態都是由正上方或左上方的格子轉移過來的。假設只有一個陣列，當開始走訪第 i 行時，該陣列儲存的仍然是第 i-1 行的狀態。

• 如果採取正序走訪，那麼走訪到 dp[i, j] 時，左上方 dp[i-1, 1] ~ dp[i-1, j-1] 值可能已經被覆蓋，此時就無法得到正確的狀態轉移結果。
• 如果採取倒序走訪，則不會發生覆蓋問題，狀態轉移可以正確進行。

下圖展示了在單個陣列下從第 i = 1 行轉換至第 i = 2 行的過程。請思考正序走訪和倒序走訪的區別。

=== "<1>"

=== "<2>"

=== "<3>"

=== "<4>"

=== "<5>"

=== "<6>"

在程式碼實現中，我們僅需將陣列 dp 的第一維 i 直接刪除，並且把內迴圈更改為倒序走訪即可：

[file]{knapsack}-[class]{}-[func]{knapsack_dp_comp}