7.3. 二叉搜索树¶

「二叉搜索树 Binary Search Tree」满足以下条件：

对于根节点，左子树中所有节点的值 \(<\) 根节点的值 \(<\) 右子树中所有节点的值；
任意节点的左子树和右子树也是二叉搜索树，即也满足条件 1. ；

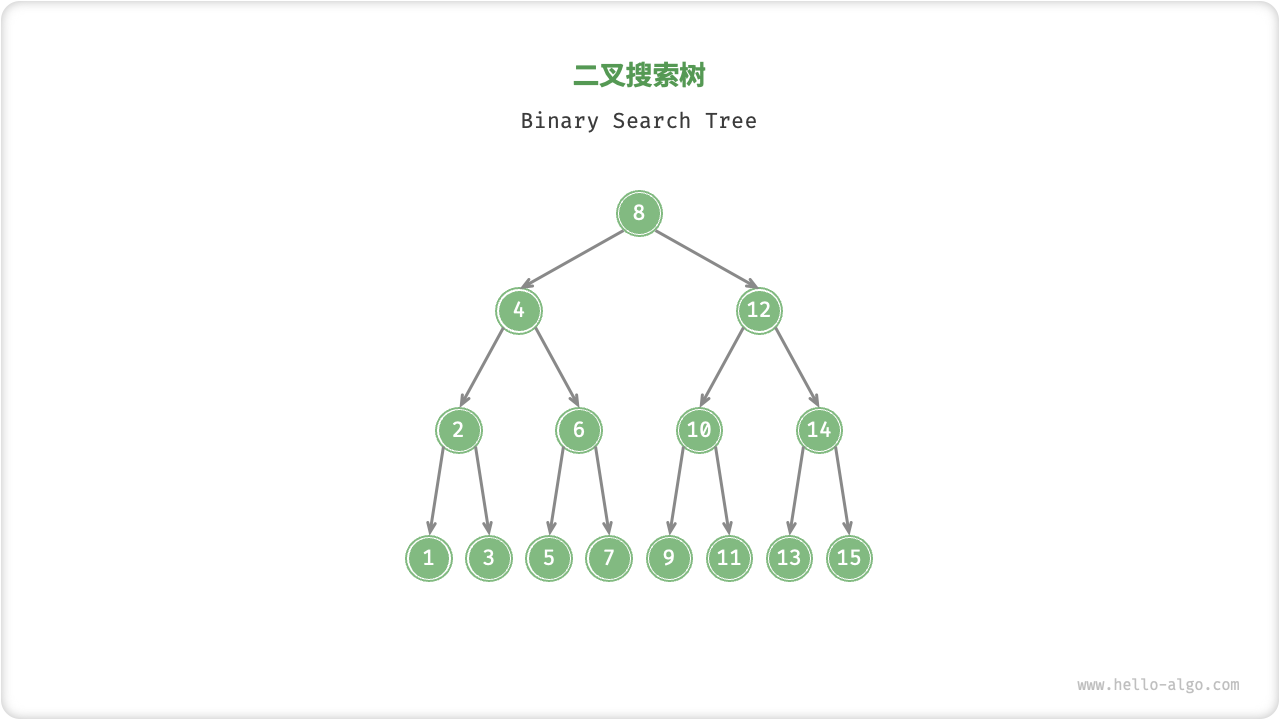
二叉搜索树

Fig. 二叉搜索树

7.3.1. 二叉搜索树的操作¶

查找节点¶

给定目标节点值 num ，可以根据二叉搜索树的性质来查找。我们声明一个节点 cur ，从二叉树的根节点 root 出发，循环比较节点值 cur.val 和 num 之间的大小关系

若 cur.val < num ，说明目标节点在 cur 的右子树中，因此执行 cur = cur.right ；
若 cur.val > num ，说明目标节点在 cur 的左子树中，因此执行 cur = cur.left ；
若 cur.val = num ，说明找到目标节点，跳出循环并返回该节点即可；

<1><2><3><4>

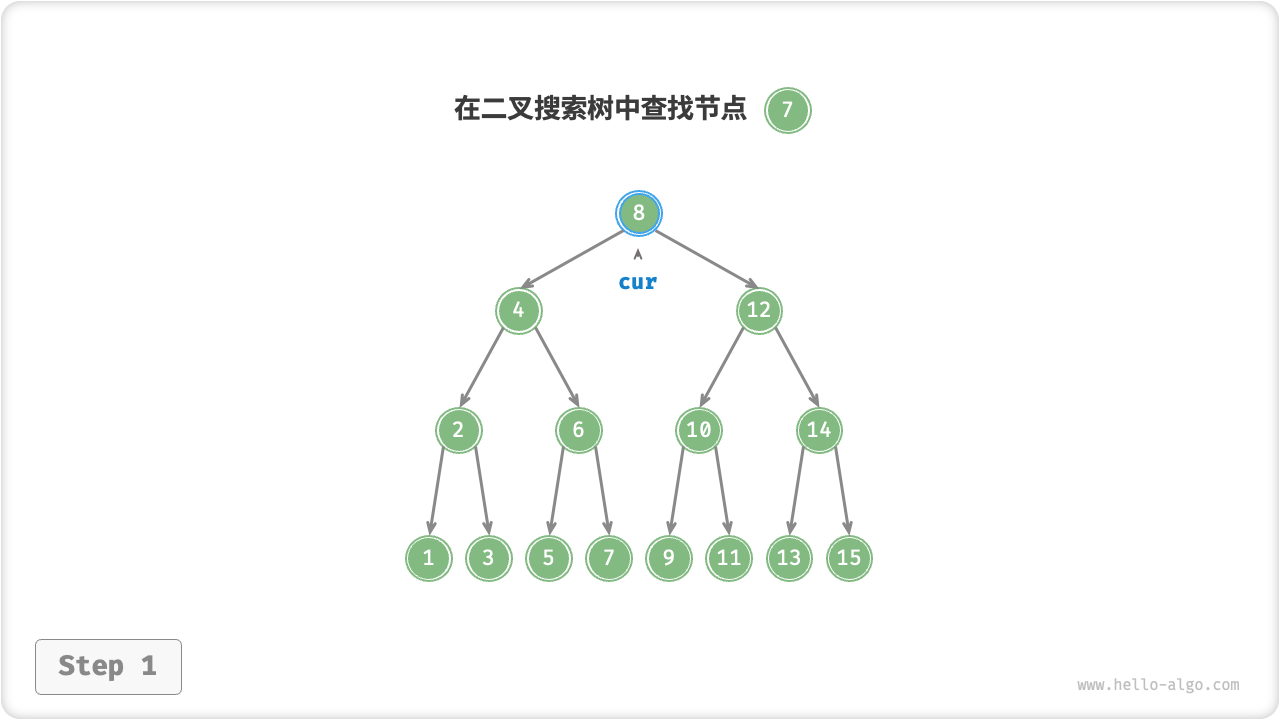
查找节点步骤

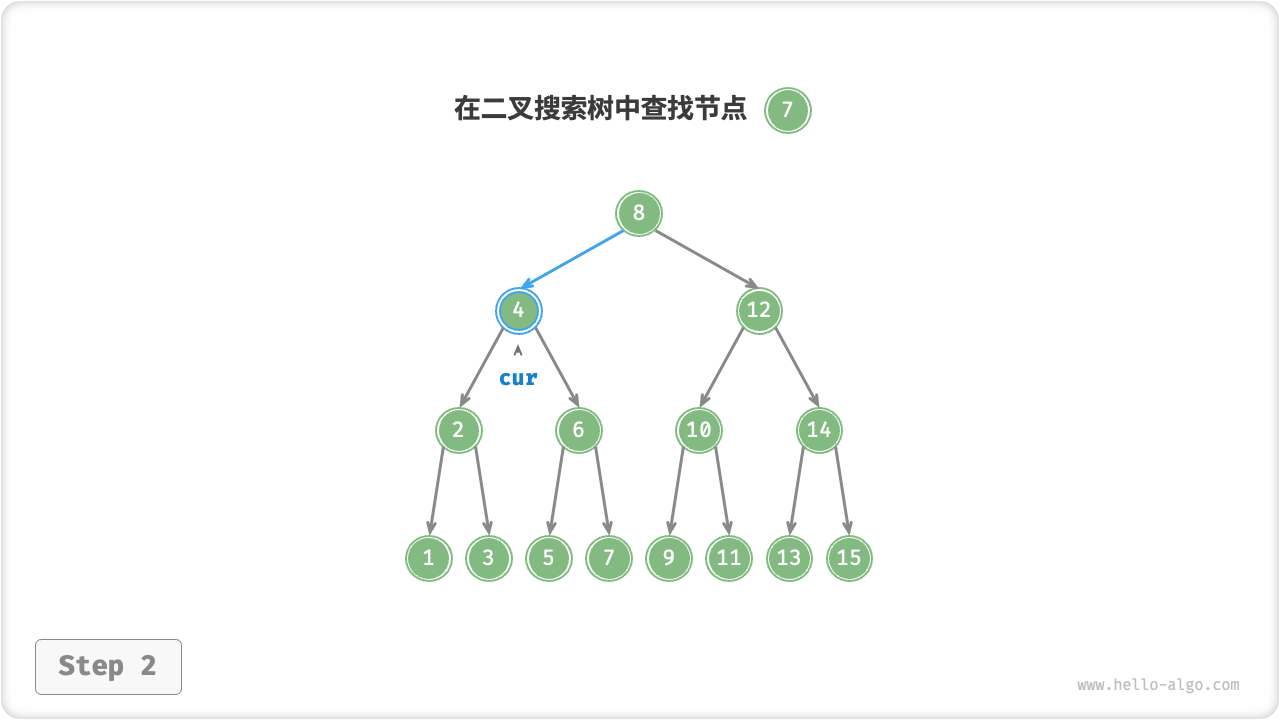
bst_search_step2

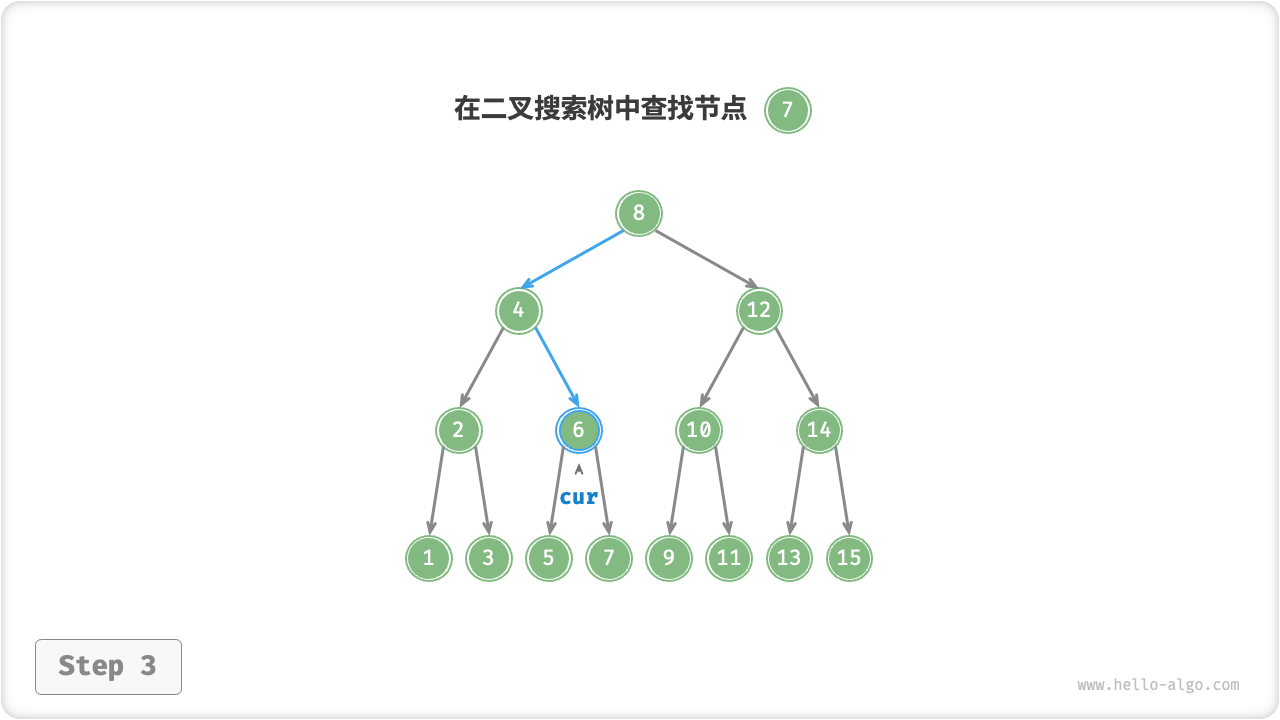
bst_search_step3

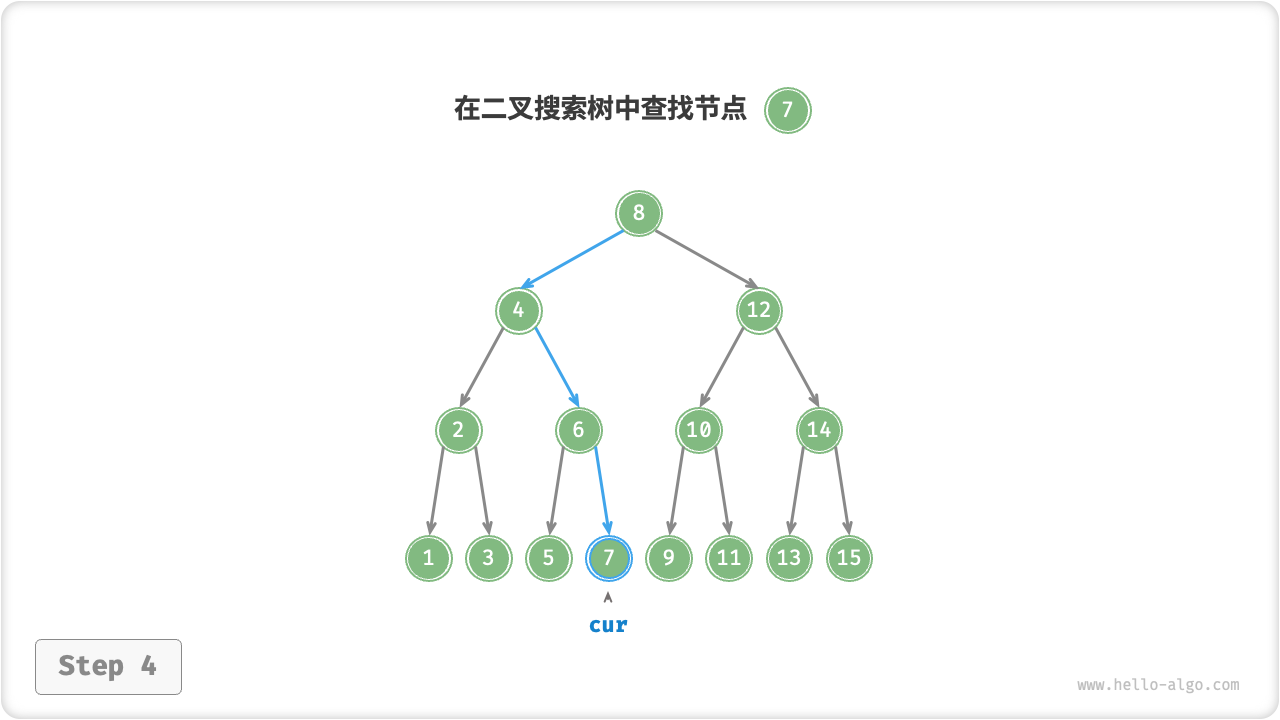
bst_search_step4

二叉搜索树的查找操作和二分查找算法如出一辙，也是在每轮排除一半情况。循环次数最多为二叉树的高度，当二叉树平衡时，使用 \(O(\log n)\) 时间。

JavaC++PythonGoJavaScriptTypeScriptCC#SwiftZig

binary_search_tree.java

/* 查找节点 */
TreeNode search(int num) {
    TreeNode cur = root;
    // 循环查找，越过叶节点后跳出
    while (cur != null) {
        // 目标节点在 cur 的右子树中
        if (cur.val < num) cur = cur.right;
        // 目标节点在 cur 的左子树中
        else if (cur.val > num) cur = cur.left;
        // 找到目标节点，跳出循环
        else break;
    }
    // 返回目标节点
    return cur;
}

binary_search_tree.cpp

/* 查找节点 */
TreeNode* search(int num) {
    TreeNode* cur = root;
    // 循环查找，越过叶节点后跳出
    while (cur != nullptr) {
        // 目标节点在 cur 的右子树中
        if (cur->val < num) cur = cur->right;
        // 目标节点在 cur 的左子树中
        else if (cur->val > num) cur = cur->left;
        // 找到目标节点，跳出循环
        else break;
    }
    // 返回目标节点
    return cur;
}

binary_search_tree.py

def search(self, num: int) -> TreeNode | None:
    """查找节点"""
    cur: TreeNode | None = self.__root
    # 循环查找，越过叶节点后跳出
    while cur is not None:
        # 目标节点在 cur 的右子树中
        if cur.val < num:
            cur = cur.right
        # 目标节点在 cur 的左子树中
        elif cur.val > num:
            cur = cur.left
        # 找到目标节点，跳出循环
        else:
            break
    return cur

binary_search_tree.go

/* 查找节点 */
func (bst *binarySearchTree) search(num int) *TreeNode {
    node := bst.root
    // 循环查找，越过叶节点后跳出
    for node != nil {
        if node.Val < num {
            // 目标节点在 cur 的右子树中
            node = node.Right
        } else if node.Val > num {
            // 目标节点在 cur 的左子树中
            node = node.Left
        } else {
            // 找到目标节点，跳出循环
            break
        }
    }
    // 返回目标节点
    return node
}

binary_search_tree.js

/* 查找节点 */
function search(num) {
    let cur = root;
    // 循环查找，越过叶节点后跳出
    while (cur !== null) {
        // 目标节点在 cur 的右子树中
        if (cur.val < num) cur = cur.right;
        // 目标节点在 cur 的左子树中
        else if (cur.val > num) cur = cur.left;
        // 找到目标节点，跳出循环
        else break;
    }
    // 返回目标节点
    return cur;
}

binary_search_tree.ts

/* 查找节点 */
function search(num: number): TreeNode | null {
    let cur = root;
    // 循环查找，越过叶节点后跳出
    while (cur !== null) {
        if (cur.val < num) {
            cur = cur.right; // 目标节点在 cur 的右子树中
        } else if (cur.val > num) {
            cur = cur.left; // 目标节点在 cur 的左子树中
        } else {
            break; // 找到目标节点，跳出循环
        }
    }
    // 返回目标节点
    return cur;
}

binary_search_tree.c

[class]{binarySearchTree}-[func]{search}

binary_search_tree.cs

/* 查找节点 */
TreeNode? search(int num)
{
    TreeNode? cur = root;
    // 循环查找，越过叶节点后跳出
    while (cur != null)
    {
        // 目标节点在 cur 的右子树中
        if (cur.val < num) cur = cur.right;
        // 目标节点在 cur 的左子树中
        else if (cur.val > num) cur = cur.left;
        // 找到目标节点，跳出循环
        else break;
    }
    // 返回目标节点
    return cur;
}

binary_search_tree.swift

/* 查找节点 */
func search(num: Int) -> TreeNode? {
    var cur = root
    // 循环查找，越过叶节点后跳出
    while cur != nil {
        // 目标节点在 cur 的右子树中
        if cur!.val < num {
            cur = cur?.right
        }
        // 目标节点在 cur 的左子树中
        else if cur!.val > num {
            cur = cur?.left
        }
        // 找到目标节点，跳出循环
        else {
            break
        }
    }
    // 返回目标节点
    return cur
}

binary_search_tree.zig

// 查找节点
fn search(self: *Self, num: T) ?*inc.TreeNode(T) {
    var cur = self.root;
    // 循环查找，越过叶节点后跳出
    while (cur != null) {
        // 目标节点在 cur 的右子树中
        if (cur.?.val < num) {
            cur = cur.?.right;
        // 目标节点在 cur 的左子树中
        } else if (cur.?.val > num) {
            cur = cur.?.left;
        // 找到目标节点，跳出循环
        } else {
            break;
        }
    }
    // 返回目标节点
    return cur;
}

插入节点¶

给定一个待插入元素 num ，为了保持二叉搜索树“左子树 < 根节点 < 右子树”的性质，插入操作分为两步：

查找插入位置：与查找操作类似，我们从根节点出发，根据当前节点值和 num 的大小关系循环向下搜索，直到越过叶节点（遍历到 \(\text{null}\) ）时跳出循环；
在该位置插入节点：初始化节点 num ，将该节点放到 \(\text{null}\) 的位置；

二叉搜索树不允许存在重复节点，否则将会违背其定义。因此若待插入节点在树中已经存在，则不执行插入，直接返回即可。

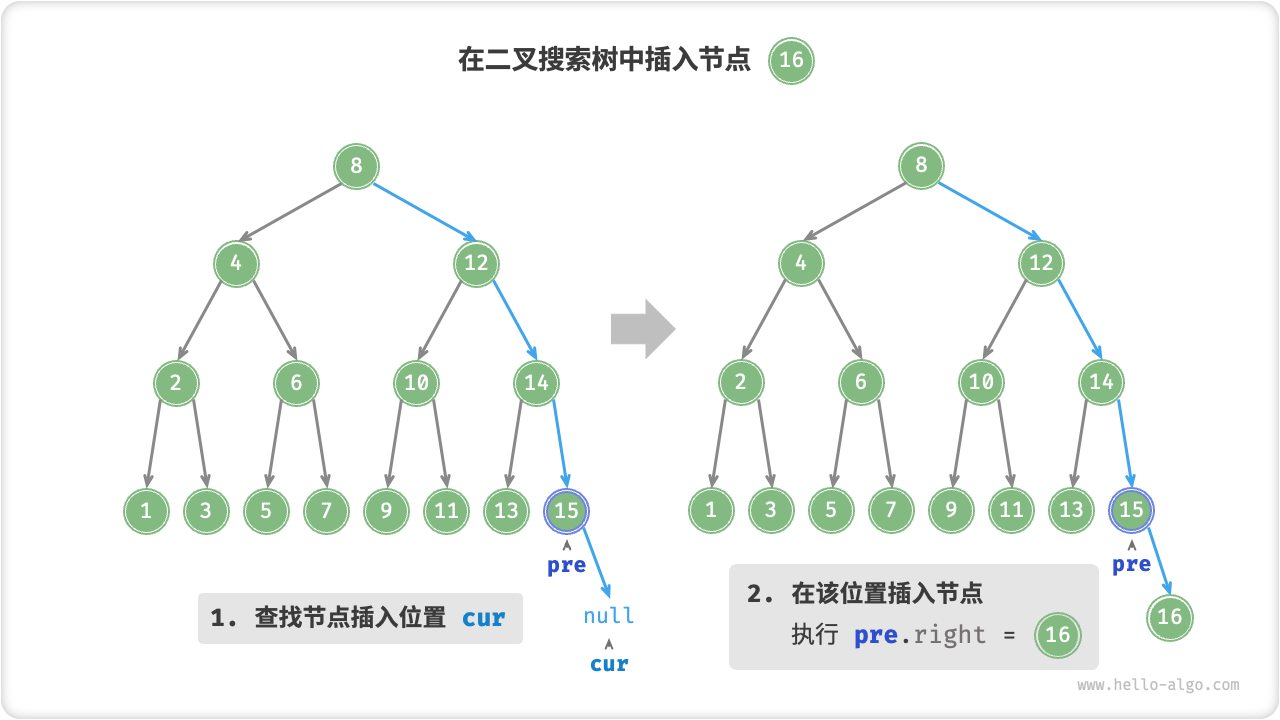
在二叉搜索树中插入节点

Fig. 在二叉搜索树中插入节点

JavaC++PythonGoJavaScriptTypeScriptCC#SwiftZig

binary_search_tree.java

/* 插入节点 */
TreeNode insert(int num) {
    // 若树为空，直接提前返回
    if (root == null) return null;
    TreeNode cur = root, pre = null;
    // 循环查找，越过叶节点后跳出
    while (cur != null) {
        // 找到重复节点，直接返回
        if (cur.val == num) return null;
        pre = cur;
        // 插入位置在 cur 的右子树中
        if (cur.val < num) cur = cur.right;
        // 插入位置在 cur 的左子树中
        else cur = cur.left;
    }
    // 插入节点 val
    TreeNode node = new TreeNode(num);
    if (pre.val < num) pre.right = node;
    else pre.left = node;
    return node;
}

binary_search_tree.cpp

/* 插入节点 */
TreeNode* insert(int num) {
    // 若树为空，直接提前返回
    if (root == nullptr) return nullptr;
    TreeNode *cur = root, *pre = nullptr;
    // 循环查找，越过叶节点后跳出
    while (cur != nullptr) {
        // 找到重复节点，直接返回
        if (cur->val == num) return nullptr;
        pre = cur;
        // 插入位置在 cur 的右子树中
        if (cur->val < num) cur = cur->right;
        // 插入位置在 cur 的左子树中
        else cur = cur->left;
    }
    // 插入节点 val
    TreeNode* node = new TreeNode(num);
    if (pre->val < num) pre->right = node;
    else pre->left = node;
    return node;
}

binary_search_tree.py

def insert(self, num: int) -> TreeNode | None:
    """插入节点"""
    # 若树为空，直接提前返回
    if self.__root is None:
        return None

    # 循环查找，越过叶节点后跳出
    cur, pre = self.__root, None
    while cur is not None:
        # 找到重复节点，直接返回
        if cur.val == num:
            return None
        pre = cur
        # 插入位置在 cur 的右子树中
        if cur.val < num:
            cur = cur.right
        # 插入位置在 cur 的左子树中
        else:
            cur = cur.left

    # 插入节点 val
    node = TreeNode(num)
    if pre.val < num:
        pre.right = node
    else:
        pre.left = node
    return node

binary_search_tree.go

/* 插入节点 */
func (bst *binarySearchTree) insert(num int) *TreeNode {
    cur := bst.root
    // 若树为空，直接提前返回
    if cur == nil {
        return nil
    }
    // 待插入节点之前的节点位置
    var pre *TreeNode = nil
    // 循环查找，越过叶节点后跳出
    for cur != nil {
        if cur.Val == num {
            return nil
        }
        pre = cur
        if cur.Val < num {
            cur = cur.Right
        } else {
            cur = cur.Left
        }
    }
    // 插入节点
    node := NewTreeNode(num)
    if pre.Val < num {
        pre.Right = node
    } else {
        pre.Left = node
    }
    return cur
}

binary_search_tree.js

/* 插入节点 */
function insert(num) {
    // 若树为空，直接提前返回
    if (root === null) return null;
    let cur = root, pre = null;
    // 循环查找，越过叶节点后跳出
    while (cur !== null) {
        // 找到重复节点，直接返回
        if (cur.val === num) return null;
        pre = cur;
        // 插入位置在 cur 的右子树中
        if (cur.val < num) cur = cur.right;
        // 插入位置在 cur 的左子树中
        else cur = cur.left;
    }
    // 插入节点 val
    let node = new TreeNode(num);
    if (pre.val < num) pre.right = node;
    else pre.left = node;
    return node;
}

binary_search_tree.ts

/* 插入节点 */
function insert(num: number): TreeNode | null {
    // 若树为空，直接提前返回
    if (root === null) {
        return null;
    }
    let cur = root,
        pre: TreeNode | null = null;
    // 循环查找，越过叶节点后跳出
    while (cur !== null) {
        if (cur.val === num) {
            return null; // 找到重复节点，直接返回
        }
        pre = cur;
        if (cur.val < num) {
            cur = cur.right as TreeNode; // 插入位置在 cur 的右子树中
        } else {
            cur = cur.left as TreeNode; // 插入位置在 cur 的左子树中
        }
    }
    // 插入节点 val
    let node = new TreeNode(num);
    if (pre!.val < num) {
        pre!.right = node;
    } else {
        pre!.left = node;
    }
    return node;
}

binary_search_tree.c

[class]{binarySearchTree}-[func]{insert}

binary_search_tree.cs

/* 插入节点 */
TreeNode? insert(int num)
{
    // 若树为空，直接提前返回
    if (root == null) return null;
    TreeNode? cur = root, pre = null;
    // 循环查找，越过叶节点后跳出
    while (cur != null)
    {
        // 找到重复节点，直接返回
        if (cur.val == num) return null;
        pre = cur;
        // 插入位置在 cur 的右子树中
        if (cur.val < num) cur = cur.right;
        // 插入位置在 cur 的左子树中
        else cur = cur.left;
    }

    // 插入节点 val
    TreeNode node = new TreeNode(num);
    if (pre != null)
    {
        if (pre.val < num) pre.right = node;
        else pre.left = node;
    }
    return node;
}

binary_search_tree.swift

/* 插入节点 */
func insert(num: Int) -> TreeNode? {
    // 若树为空，直接提前返回
    if root == nil {
        return nil
    }
    var cur = root
    var pre: TreeNode?
    // 循环查找，越过叶节点后跳出
    while cur != nil {
        // 找到重复节点，直接返回
        if cur!.val == num {
            return nil
        }
        pre = cur
        // 插入位置在 cur 的右子树中
        if cur!.val < num {
            cur = cur?.right
        }
        // 插入位置在 cur 的左子树中
        else {
            cur = cur?.left
        }
    }
    // 插入节点 val
    let node = TreeNode(x: num)
    if pre!.val < num {
        pre?.right = node
    } else {
        pre?.left = node
    }
    return node
}

binary_search_tree.zig

// 插入节点
fn insert(self: *Self, num: T) !?*inc.TreeNode(T) {
    // 若树为空，直接提前返回
    if (self.root == null) return null;
    var cur = self.root;
    var pre: ?*inc.TreeNode(T) = null;
    // 循环查找，越过叶节点后跳出
    while (cur != null) {
        // 找到重复节点，直接返回
        if (cur.?.val == num) return null;
        pre = cur;
        // 插入位置在 cur 的右子树中
        if (cur.?.val < num) {
            cur = cur.?.right;
        // 插入位置在 cur 的左子树中
        } else {
            cur = cur.?.left;
        }
    }
    // 插入节点 val
    var node = try self.mem_allocator.create(inc.TreeNode(T));
    node.init(num);
    if (pre.?.val < num) {
        pre.?.right = node;
    } else {
        pre.?.left = node;
    }
    return node;
}

为了插入节点，需要借助 辅助节点 pre 保存上一轮循环的节点，这样在遍历到 \(\text{null}\) 时，我们也可以获取到其父节点，从而完成节点插入操作。

与查找节点相同，插入节点使用 \(O(\log n)\) 时间。

删除节点¶

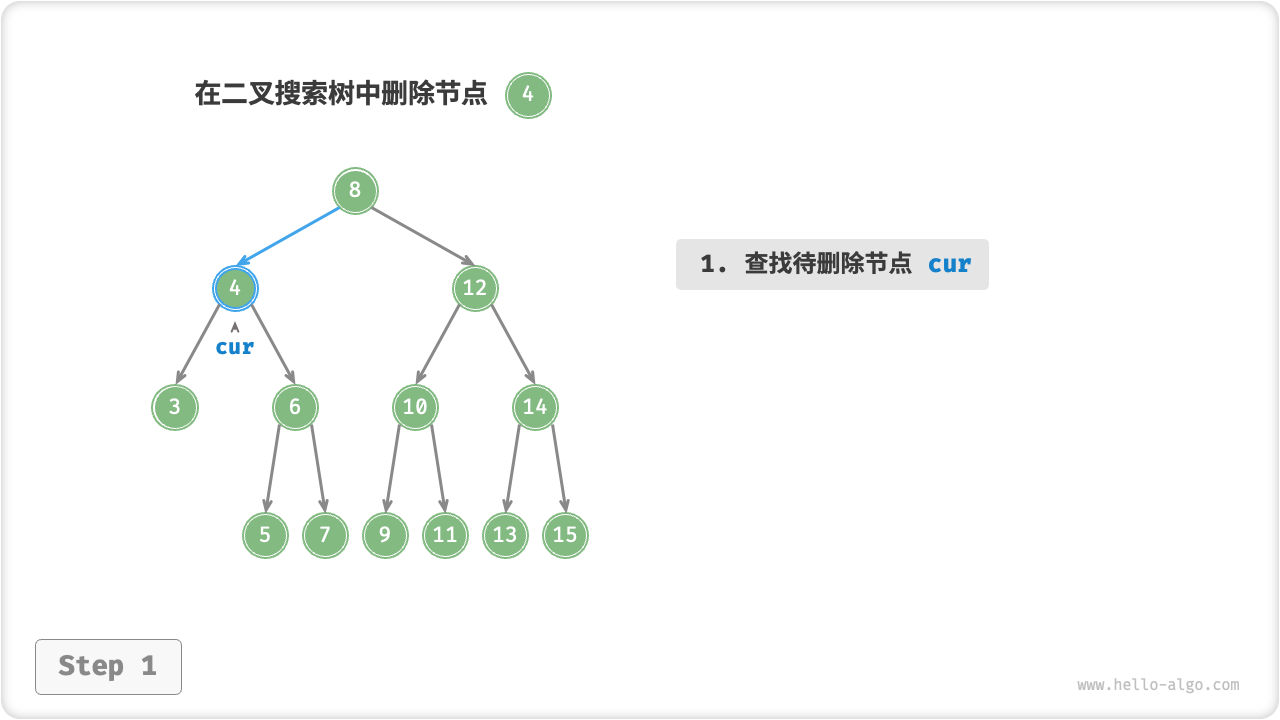
与插入节点一样，我们需要在删除操作后维持二叉搜索树的“左子树 < 根节点 < 右子树”的性质。首先，我们需要在二叉树中执行查找操作，获取待删除节点。接下来，根据待删除节点的子节点数量，删除操作需要分为三种情况：

当待删除节点的子节点数量 \(= 0\) 时，表明待删除节点是叶节点，直接删除即可。

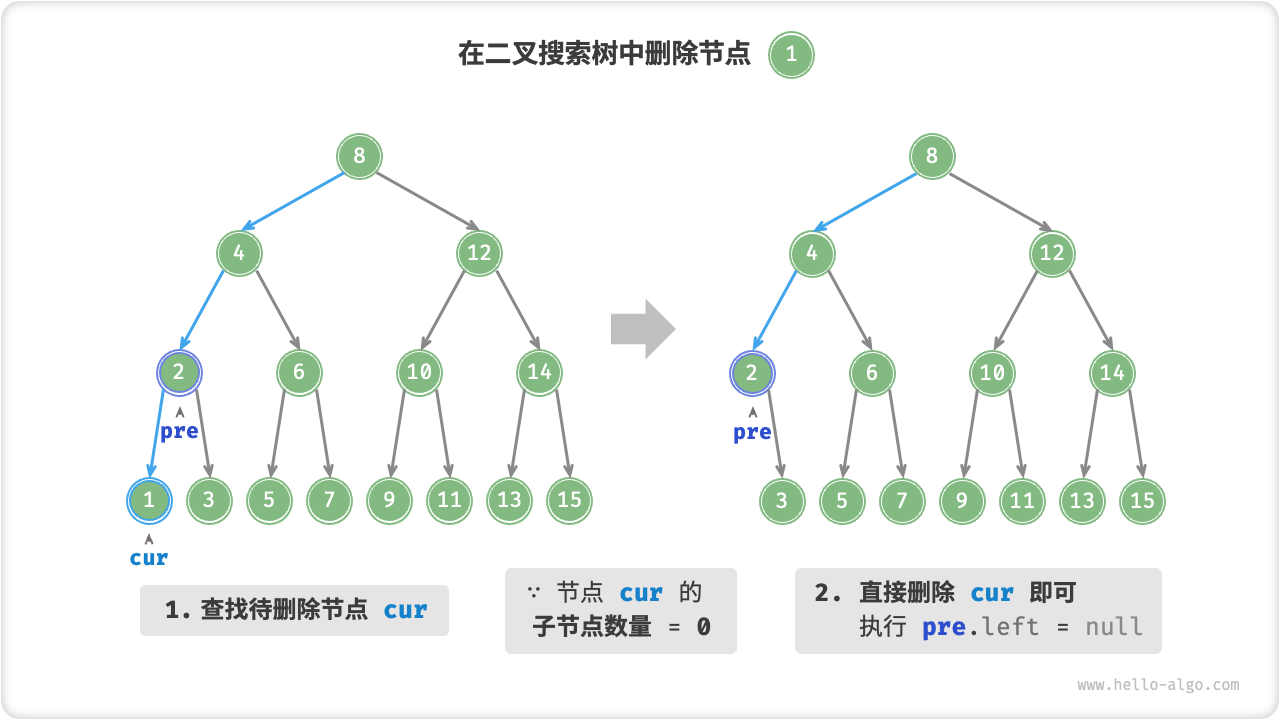
在二叉搜索树中删除节点（度为 0）

Fig. 在二叉搜索树中删除节点（度为 0）

当待删除节点的子节点数量 \(= 1\) 时，将待删除节点替换为其子节点即可。

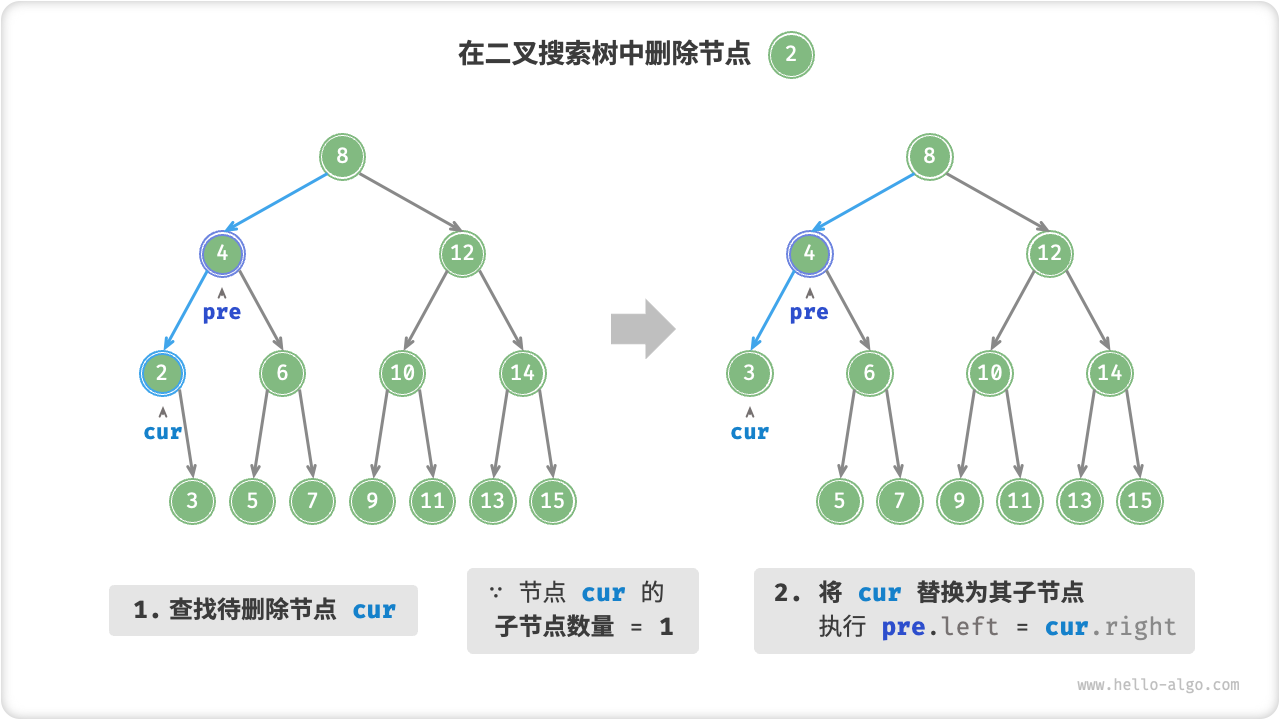
在二叉搜索树中删除节点（度为 1）

Fig. 在二叉搜索树中删除节点（度为 1）

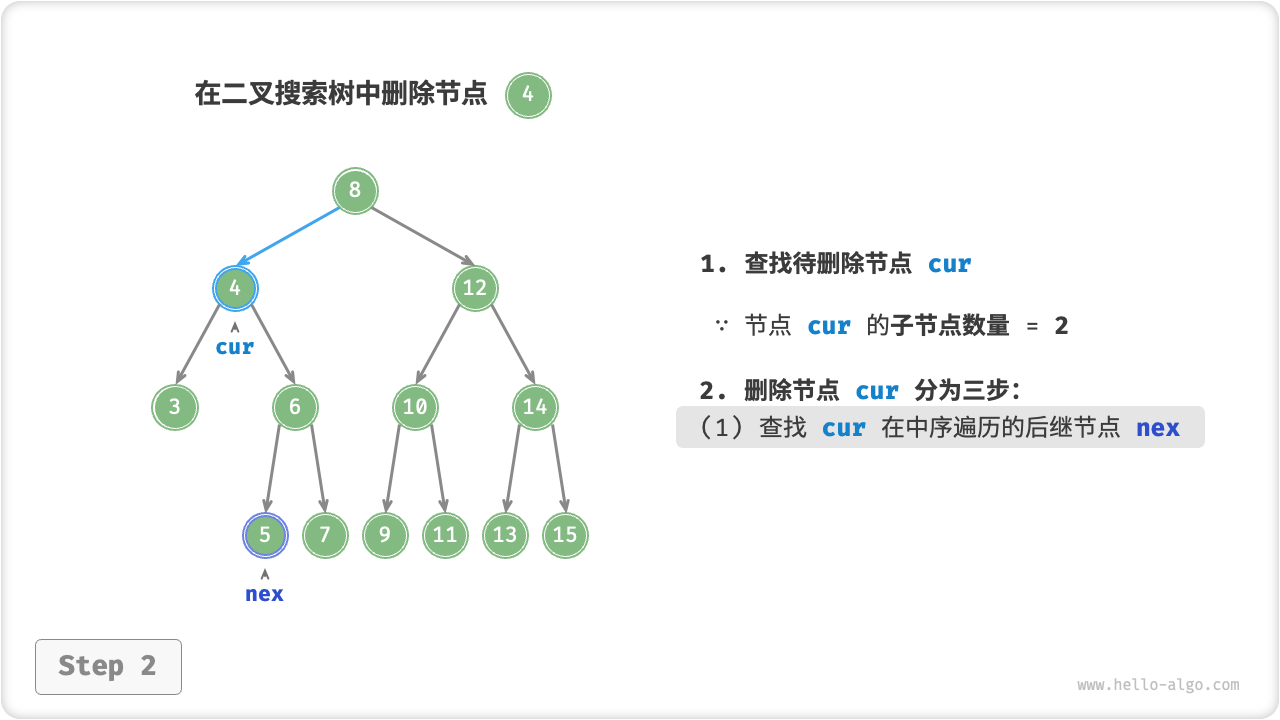
当待删除节点的子节点数量 \(= 2\) 时，删除操作分为三步：

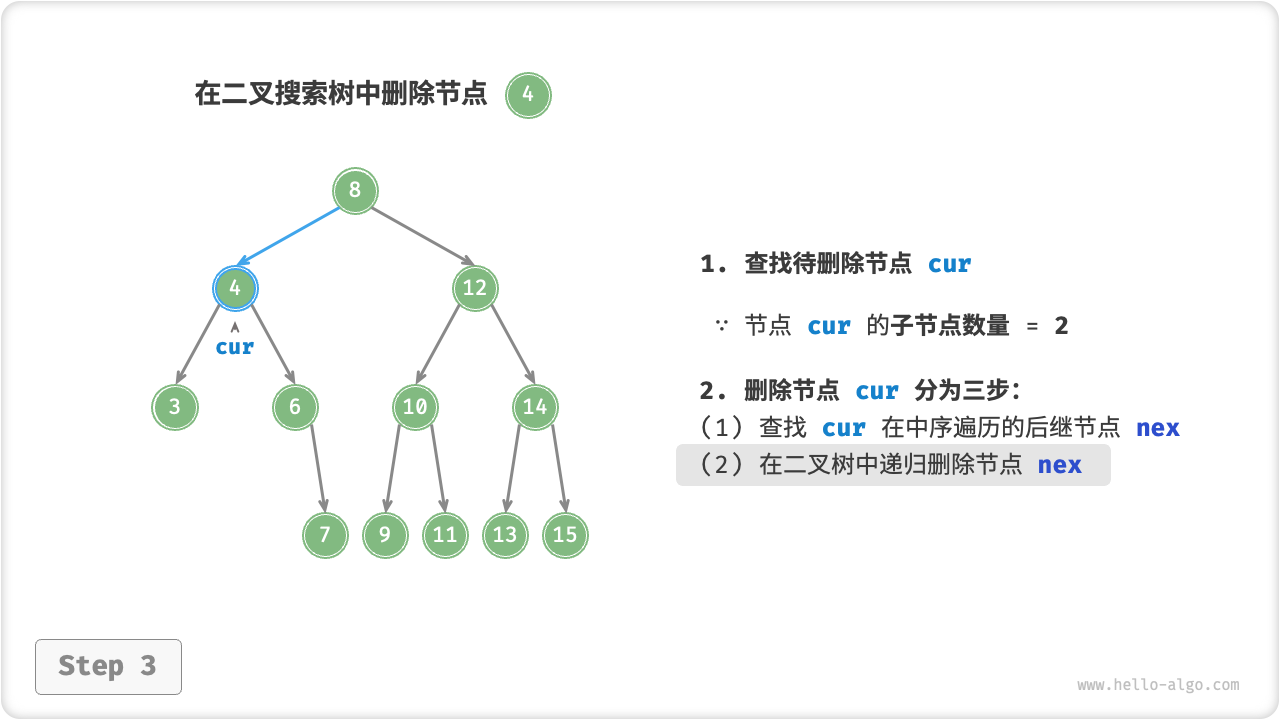
找到待删除节点在 中序遍历序列 中的下一个节点，记为 nex ；
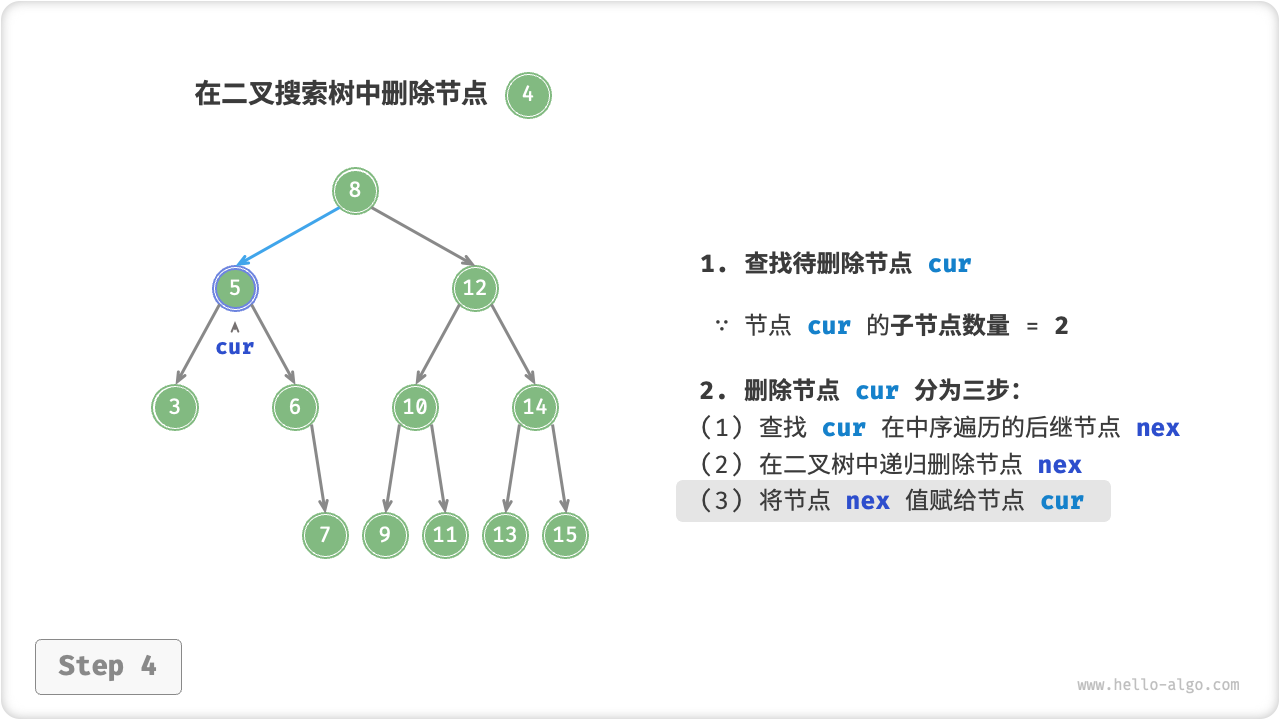
在树中递归删除节点 nex ；
使用 nex 替换待删除节点；

<1><2><3><4>

删除节点（度为 2）步骤

bst_remove_case3_step2

bst_remove_case3_step3

bst_remove_case3_step4

删除节点操作也使用 \(O(\log n)\) 时间，其中查找待删除节点 \(O(\log n)\) ，获取中序遍历后继节点 \(O(\log n)\) 。

JavaC++PythonGoJavaScriptTypeScriptCC#SwiftZig

binary_search_tree.java

/* 删除节点 */
TreeNode remove(int num) {
    // 若树为空，直接提前返回
    if (root == null) return null;
    TreeNode cur = root, pre = null;
    // 循环查找，越过叶节点后跳出
    while (cur != null) {
        // 找到待删除节点，跳出循环
        if (cur.val == num) break;
        pre = cur;
        // 待删除节点在 cur 的右子树中
        if (cur.val < num) cur = cur.right;
        // 待删除节点在 cur 的左子树中
        else cur = cur.left;
    }
    // 若无待删除节点，则直接返回
    if (cur == null) return null;
    // 子节点数量 = 0 or 1
    if (cur.left == null || cur.right == null) {
        // 当子节点数量 = 0 / 1 时， child = null / 该子节点
        TreeNode child = cur.left != null ? cur.left : cur.right;
        // 删除节点 cur
        if (pre.left == cur) pre.left = child;
        else pre.right = child;
    }
    // 子节点数量 = 2
    else {
        // 获取中序遍历中 cur 的下一个节点
        TreeNode nex = getInOrderNext(cur.right);
        int tmp = nex.val;
        // 递归删除节点 nex
        remove(nex.val);
        // 将 nex 的值复制给 cur
        cur.val = tmp;
    }
    return cur;
}

/* 获取中序遍历中的下一个节点（仅适用于 root 有左子节点的情况） */
TreeNode getInOrderNext(TreeNode root) {
    if (root == null) return root;
    // 循环访问左子节点，直到叶节点时为最小节点，跳出
    while (root.left != null) {
        root = root.left;
    }
    return root;
}

binary_search_tree.cpp

/* 删除节点 */
TreeNode* remove(int num) {
    // 若树为空，直接提前返回
    if (root == nullptr) return nullptr;
    TreeNode *cur = root, *pre = nullptr;
    // 循环查找，越过叶节点后跳出
    while (cur != nullptr) {
        // 找到待删除节点，跳出循环
        if (cur->val == num) break;
        pre = cur;
        // 待删除节点在 cur 的右子树中
        if (cur->val < num) cur = cur->right;
        // 待删除节点在 cur 的左子树中
        else cur = cur->left;
    }
    // 若无待删除节点，则直接返回
    if (cur == nullptr) return nullptr;
    // 子节点数量 = 0 or 1
    if (cur->left == nullptr || cur->right == nullptr) {
        // 当子节点数量 = 0 / 1 时， child = nullptr / 该子节点
        TreeNode* child = cur->left != nullptr ? cur->left : cur->right;
        // 删除节点 cur
        if (pre->left == cur) pre->left = child;
        else pre->right = child;
        // 释放内存
        delete cur;
    }
    // 子节点数量 = 2
    else {
        // 获取中序遍历中 cur 的下一个节点
        TreeNode* nex = getInOrderNext(cur->right);
        int tmp = nex->val;
        // 递归删除节点 nex
        remove(nex->val);
        // 将 nex 的值复制给 cur
        cur->val = tmp;
    }
    return cur;
}

/* 获取中序遍历中的下一个节点（仅适用于 root 有左子节点的情况） */
TreeNode* getInOrderNext(TreeNode* root) {
    if (root == nullptr) return root;
    // 循环访问左子节点，直到叶节点时为最小节点，跳出
    while (root->left != nullptr) {
        root = root->left;
    }
    return root;
}

binary_search_tree.py

def remove(self, num: int) -> TreeNode | None:
    """删除节点"""
    # 若树为空，直接提前返回
    if self.__root is None:
        return None

    # 循环查找，越过叶节点后跳出
    cur, pre = self.__root, None
    while cur is not None:
        # 找到待删除节点，跳出循环
        if cur.val == num:
            break
        pre = cur
        if cur.val < num:  # 待删除节点在 cur 的右子树中
            cur = cur.right
        else:  # 待删除节点在 cur 的左子树中
            cur = cur.left
    # 若无待删除节点，则直接返回
    if cur is None:
        return None

    # 子节点数量 = 0 or 1
    if cur.left is None or cur.right is None:
        # 当子节点数量 = 0 / 1 时， child = null / 该子节点
        child = cur.left or cur.right
        # 删除节点 cur
        if pre.left == cur:
            pre.left = child
        else:
            pre.right = child
    # 子节点数量 = 2
    else:
        # 获取中序遍历中 cur 的下一个节点
        nex: TreeNode = self.get_inorder_next(cur.right)
        tmp: int = nex.val
        # 递归删除节点 nex
        self.remove(nex.val)
        # 将 nex 的值复制给 cur
        cur.val = tmp
    return cur

def get_inorder_next(self, root: TreeNode | None) -> TreeNode | None:
    """获取中序遍历中的下一个节点（仅适用于 root 有左子节点的情况）"""
    if root is None:
        return root
    # 循环访问左子节点，直到叶节点时为最小节点，跳出
    while root.left is not None:
        root = root.left
    return root

binary_search_tree.go

/* 删除节点 */
func (bst *binarySearchTree) remove(num int) *TreeNode {
    cur := bst.root
    // 若树为空，直接提前返回
    if cur == nil {
        return nil
    }
    // 待删除节点之前的节点位置
    var pre *TreeNode = nil
    // 循环查找，越过叶节点后跳出
    for cur != nil {
        if cur.Val == num {
            break
        }
        pre = cur
        if cur.Val < num {
            // 待删除节点在右子树中
            cur = cur.Right
        } else {
            // 待删除节点在左子树中
            cur = cur.Left
        }
    }
    // 若无待删除节点，则直接返回
    if cur == nil {
        return nil
    }
    // 子节点数为 0 或 1
    if cur.Left == nil || cur.Right == nil {
        var child *TreeNode = nil
        // 取出待删除节点的子节点
        if cur.Left != nil {
            child = cur.Left
        } else {
            child = cur.Right
        }
        // 将子节点替换为待删除节点
        if pre.Left == cur {
            pre.Left = child
        } else {
            pre.Right = child
        }
        // 子节点数为 2
    } else {
        // 获取中序遍历中待删除节点 cur 的下一个节点
        next := bst.getInOrderNext(cur)
        temp := next.Val
        // 递归删除节点 next
        bst.remove(next.Val)
        // 将 next 的值复制给 cur
        cur.Val = temp
    }
    return cur
}

/* 获取中序遍历的下一个节点（仅适用于 root 有左子节点的情况） */
func (bst *binarySearchTree) getInOrderNext(node *TreeNode) *TreeNode {
    if node == nil {
        return node
    }
    // 循环访问左子节点，直到叶节点时为最小节点，跳出
    for node.Left != nil {
        node = node.Left
    }
    return node
}

binary_search_tree.js

/* 删除节点 */
function remove(num) {
    // 若树为空，直接提前返回
    if (root === null) return null;
    let cur = root, pre = null;
    // 循环查找，越过叶节点后跳出
    while (cur !== null) {
        // 找到待删除节点，跳出循环
        if (cur.val === num) break;
        pre = cur;
        // 待删除节点在 cur 的右子树中
        if (cur.val < num) cur = cur.right;
        // 待删除节点在 cur 的左子树中
        else cur = cur.left;
    }
    // 若无待删除节点，则直接返回
    if (cur === null) return null;
    // 子节点数量 = 0 or 1
    if (cur.left === null || cur.right === null) {
        // 当子节点数量 = 0 / 1 时， child = null / 该子节点
        let child = cur.left !== null ? cur.left : cur.right;
        // 删除节点 cur
        if (pre.left === cur) pre.left = child;
        else pre.right = child;
    }
    // 子节点数量 = 2
    else {
        // 获取中序遍历中 cur 的下一个节点
        let nex = getInOrderNext(cur.right);
        let tmp = nex.val;
        // 递归删除节点 nex
        remove(nex.val);
        // 将 nex 的值复制给 cur
        cur.val = tmp;
    }
    return cur;
}

/* 获取中序遍历中的下一个节点（仅适用于 root 有左子节点的情况） */
function getInOrderNext(root) {
    if (root === null) return root;
    // 循环访问左子节点，直到叶节点时为最小节点，跳出
    while (root.left !== null) {
        root = root.left;
    }
    return root;
}

binary_search_tree.ts

/* 删除节点 */
function remove(num: number): TreeNode | null {
    // 若树为空，直接提前返回
    if (root === null) {
        return null;
    }
    let cur = root,
        pre: TreeNode | null = null;
    // 循环查找，越过叶节点后跳出
    while (cur !== null) {
        // 找到待删除节点，跳出循环
        if (cur.val === num) {
            break;
        }
        pre = cur;
        if (cur.val < num) {
            cur = cur.right as TreeNode; // 待删除节点在 cur 的右子树中
        } else {
            cur = cur.left as TreeNode; // 待删除节点在 cur 的左子树中
        }
    }
    // 若无待删除节点，则直接返回
    if (cur === null) {
        return null;
    }
    // 子节点数量 = 0 or 1
    if (cur.left === null || cur.right === null) {
        // 当子节点数量 = 0 / 1 时， child = null / 该子节点
        let child = cur.left !== null ? cur.left : cur.right;
        // 删除节点 cur
        if (pre!.left === cur) {
            pre!.left = child;
        } else {
            pre!.right = child;
        }
    }
    // 子节点数量 = 2
    else {
        // 获取中序遍历中 cur 的下一个节点
        let next = getInOrderNext(cur.right);
        let tmp = next!.val;
        // 递归删除节点 nex
        remove(next!.val);
        // 将 nex 的值复制给 cur
        cur.val = tmp;
    }
    return cur;
}

/* 获取中序遍历中的下一个节点（仅适用于 root 有左子节点的情况） */
function getInOrderNext(root: TreeNode | null): TreeNode | null {
    if (root === null) {
        return null;
    }
    // 循环访问左子节点，直到叶节点时为最小节点，跳出
    while (root.left !== null) {
        root = root.left;
    }
    return root;
}

binary_search_tree.c

[class]{binarySearchTree}-[func]{remove}

[class]{binarySearchTree}-[func]{getInOrderNext}

binary_search_tree.cs

/* 删除节点 */
TreeNode? remove(int num)
{
    // 若树为空，直接提前返回
    if (root == null) return null;
    TreeNode? cur = root, pre = null;
    // 循环查找，越过叶节点后跳出
    while (cur != null)
    {
        // 找到待删除节点，跳出循环
        if (cur.val == num) break;
        pre = cur;
        // 待删除节点在 cur 的右子树中
        if (cur.val < num) cur = cur.right;
        // 待删除节点在 cur 的左子树中
        else cur = cur.left;
    }
    // 若无待删除节点，则直接返回
    if (cur == null || pre == null) return null;
    // 子节点数量 = 0 or 1
    if (cur.left == null || cur.right == null)
    {
        // 当子节点数量 = 0 / 1 时， child = null / 该子节点
        TreeNode? child = cur.left != null ? cur.left : cur.right;
        // 删除节点 cur
        if (pre.left == cur)
        {
            pre.left = child;
        }
        else
        {
            pre.right = child;
        }
    }
    // 子节点数量 = 2
    else
    {
        // 获取中序遍历中 cur 的下一个节点
        TreeNode? nex = getInOrderNext(cur.right);
        if (nex != null)
        {
            int tmp = nex.val;
            // 递归删除节点 nex
            remove(nex.val);
            // 将 nex 的值复制给 cur
            cur.val = tmp;
        }
    }
    return cur;
}

/* 获取中序遍历中的下一个节点（仅适用于 root 有左子节点的情况） */
TreeNode? getInOrderNext(TreeNode? root)
{
    if (root == null) return root;
    // 循环访问左子节点，直到叶节点时为最小节点，跳出
    while (root.left != null)
    {
        root = root.left;
    }
    return root;
}

binary_search_tree.swift

/* 删除节点 */
@discardableResult
func remove(num: Int) -> TreeNode? {
    // 若树为空，直接提前返回
    if root == nil {
        return nil
    }
    var cur = root
    var pre: TreeNode?
    // 循环查找，越过叶节点后跳出
    while cur != nil {
        // 找到待删除节点，跳出循环
        if cur!.val == num {
            break
        }
        pre = cur
        // 待删除节点在 cur 的右子树中
        if cur!.val < num {
            cur = cur?.right
        }
        // 待删除节点在 cur 的左子树中
        else {
            cur = cur?.left
        }
    }
    // 若无待删除节点，则直接返回
    if cur == nil {
        return nil
    }
    // 子节点数量 = 0 or 1
    if cur?.left == nil || cur?.right == nil {
        // 当子节点数量 = 0 / 1 时， child = null / 该子节点
        let child = cur?.left != nil ? cur?.left : cur?.right
        // 删除节点 cur
        if pre?.left === cur {
            pre?.left = child
        } else {
            pre?.right = child
        }
    }
    // 子节点数量 = 2
    else {
        // 获取中序遍历中 cur 的下一个节点
        let nex = getInOrderNext(root: cur?.right)
        let tmp = nex!.val
        // 递归删除节点 nex
        remove(num: nex!.val)
        // 将 nex 的值复制给 cur
        cur?.val = tmp
    }
    return cur
}

/* 获取中序遍历中的下一个节点（仅适用于 root 有左子节点的情况） */
func getInOrderNext(root: TreeNode?) -> TreeNode? {
    var root = root
    if root == nil {
        return root
    }
    // 循环访问左子节点，直到叶节点时为最小节点，跳出
    while root?.left != nil {
        root = root?.left
    }
    return root
}

binary_search_tree.zig

// 删除节点
fn remove(self: *Self, num: T) ?*inc.TreeNode(T) {
    // 若树为空，直接提前返回
    if (self.root == null) return null;
    var cur = self.root;
    var pre: ?*inc.TreeNode(T) = null;
    // 循环查找，越过叶节点后跳出
    while (cur != null) {
        // 找到待删除节点，跳出循环
        if (cur.?.val == num) break;
        pre = cur;
        // 待删除节点在 cur 的右子树中
        if (cur.?.val < num) {
            cur = cur.?.right;
        // 待删除节点在 cur 的左子树中
        } else {
            cur = cur.?.left;
        }
    }
    // 若无待删除节点，则直接返回
    if (cur == null) return null;
    // 子节点数量 = 0 or 1
    if (cur.?.left == null or cur.?.right == null) {
        // 当子节点数量 = 0 / 1 时， child = null / 该子节点
        var child = if (cur.?.left != null) cur.?.left else cur.?.right;
        // 删除节点 cur
        if (pre.?.left == cur) {
            pre.?.left = child;
        } else {
            pre.?.right = child;
        }
    // 子节点数量 = 2
    } else {
        // 获取中序遍历中 cur 的下一个节点
        var nex = self.getInOrderNext(cur.?.right);
        var tmp = nex.?.val;
        // 递归删除节点 nex
        _ = self.remove(nex.?.val);
        // 将 nex 的值复制给 cur
        cur.?.val = tmp;
    }
    return cur;
}

// 获取中序遍历中的下一个节点（仅适用于 root 有左子节点的情况）
fn getInOrderNext(self: *Self, node: ?*inc.TreeNode(T)) ?*inc.TreeNode(T) {
    _ = self;
    var node_tmp = node;
    if (node_tmp == null) return null;
    // 循环访问左子节点，直到叶节点时为最小节点，跳出
    while (node_tmp.?.left != null) {
        node_tmp = node_tmp.?.left;
    }
    return node_tmp;
}

排序¶

我们知道，「中序遍历」遵循“左 \(\rightarrow\) 根 \(\rightarrow\) 右”的遍历优先级，而二叉搜索树遵循“左子节点 \(<\) 根节点 \(<\) 右子节点”的大小关系。因此，在二叉搜索树中进行中序遍历时，总是会优先遍历下一个最小节点，从而得出一条重要性质：二叉搜索树的中序遍历序列是升序的。

借助中序遍历升序的性质，我们在二叉搜索树中获取有序数据仅需 \(O(n)\) 时间，而无需额外排序，非常高效。

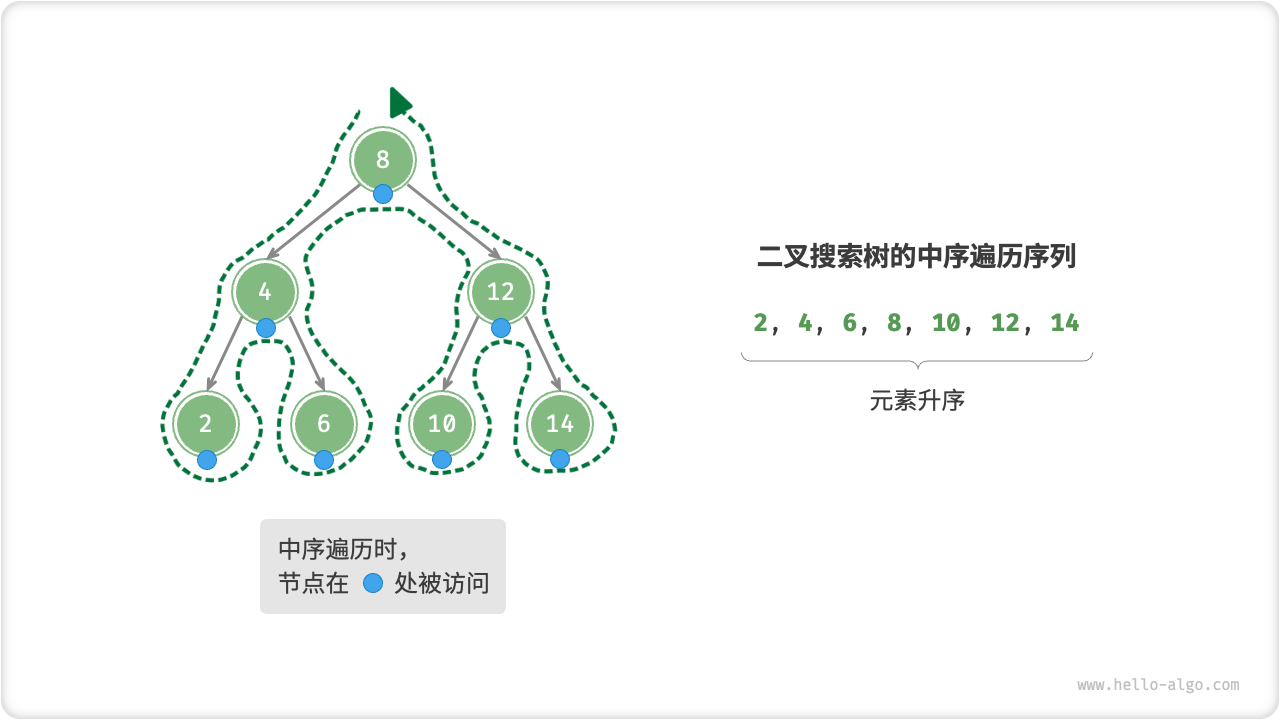
二叉搜索树的中序遍历序列

Fig. 二叉搜索树的中序遍历序列

7.3.2. 二叉搜索树的效率¶

假设给定 \(n\) 个数字，最常用的存储方式是「数组」，那么对于这串乱序的数字，常见操作的效率为：

查找元素：由于数组是无序的，因此需要遍历数组来确定，使用 \(O(n)\) 时间；
插入元素：只需将元素添加至数组尾部即可，使用 \(O(1)\) 时间；
删除元素：先查找元素，使用 \(O(n)\) 时间，再在数组中删除该元素，使用 \(O(n)\) 时间；
获取最小 / 最大元素：需要遍历数组来确定，使用 \(O(n)\) 时间；

为了得到先验信息，我们也可以预先将数组元素进行排序，得到一个「排序数组」，此时操作效率为：

查找元素：由于数组已排序，可以使用二分查找，平均使用 \(O(\log n)\) 时间；
插入元素：先查找插入位置，使用 \(O(\log n)\) 时间，再插入到指定位置，使用 \(O(n)\) 时间；
删除元素：先查找元素，使用 \(O(\log n)\) 时间，再在数组中删除该元素，使用 \(O(n)\) 时间；
获取最小 / 最大元素：数组头部和尾部元素即是最小和最大元素，使用 \(O(1)\) 时间；

观察发现，无序数组和有序数组中的各项操作的时间复杂度是“偏科”的，即有的快有的慢；而二叉搜索树的各项操作的时间复杂度都是对数阶，在数据量 \(n\) 很大时有巨大优势。

	无序数组	有序数组	二叉搜索树
查找指定元素	\(O(n)\)	\(O(\log n)\)	\(O(\log n)\)
插入元素	\(O(1)\)	\(O(n)\)	\(O(\log n)\)
删除元素	\(O(n)\)	\(O(n)\)	\(O(\log n)\)
获取最小 / 最大元素	\(O(n)\)	\(O(1)\)	\(O(\log n)\)

7.3.3. 二叉搜索树的退化¶

理想情况下，我们希望二叉搜索树的是“左右平衡”的（详见「平衡二叉树」章节），此时可以在 \(\log n\) 轮循环内查找任意节点。

如果我们动态地在二叉搜索树中插入与删除节点，则可能导致二叉树退化为链表，此时各种操作的时间复杂度也退化之 \(O(n)\) 。

Note

在实际应用中，如何保持二叉搜索树的平衡，也是一个需要重要考虑的问题。

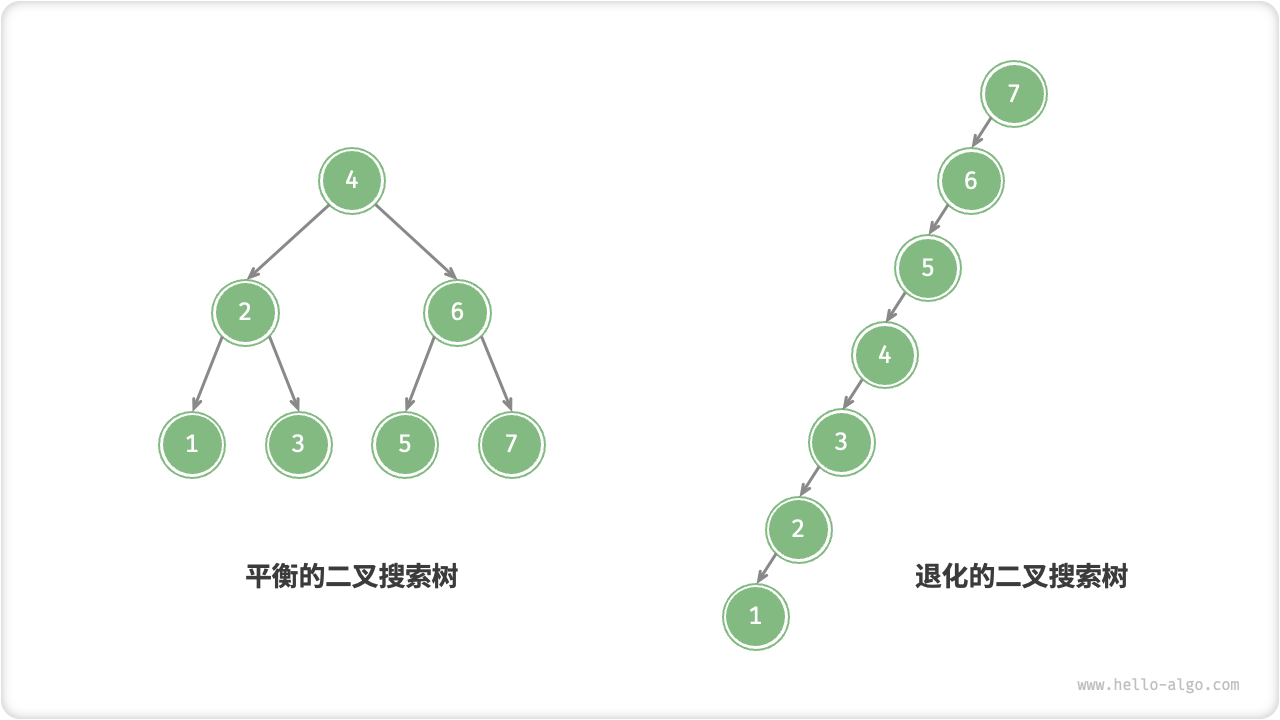
二叉搜索树的平衡与退化

Fig. 二叉搜索树的平衡与退化

7.3.4. 二叉搜索树常见应用¶

系统中的多级索引，高效查找、插入、删除操作。
各种搜索算法的底层数据结构。
存储数据流，保持其已排序。

7.3. 二叉搜索树¶

7.3.1. 二叉搜索树的操作¶

查找节点¶

插入节点¶

删除节点¶

排序¶

7.3.2. 二叉搜索树的效率¶

7.3.3. 二叉搜索树的退化¶

7.3.4. 二叉搜索树常见应用¶

评论