12.4   Tower of Hanoi Problem

In both merge sorting and building binary trees, we decompose the original problem into two subproblems, each half the size of the original problem. However, for the Tower of Hanoi, we adopt a different decomposition strategy.

Question

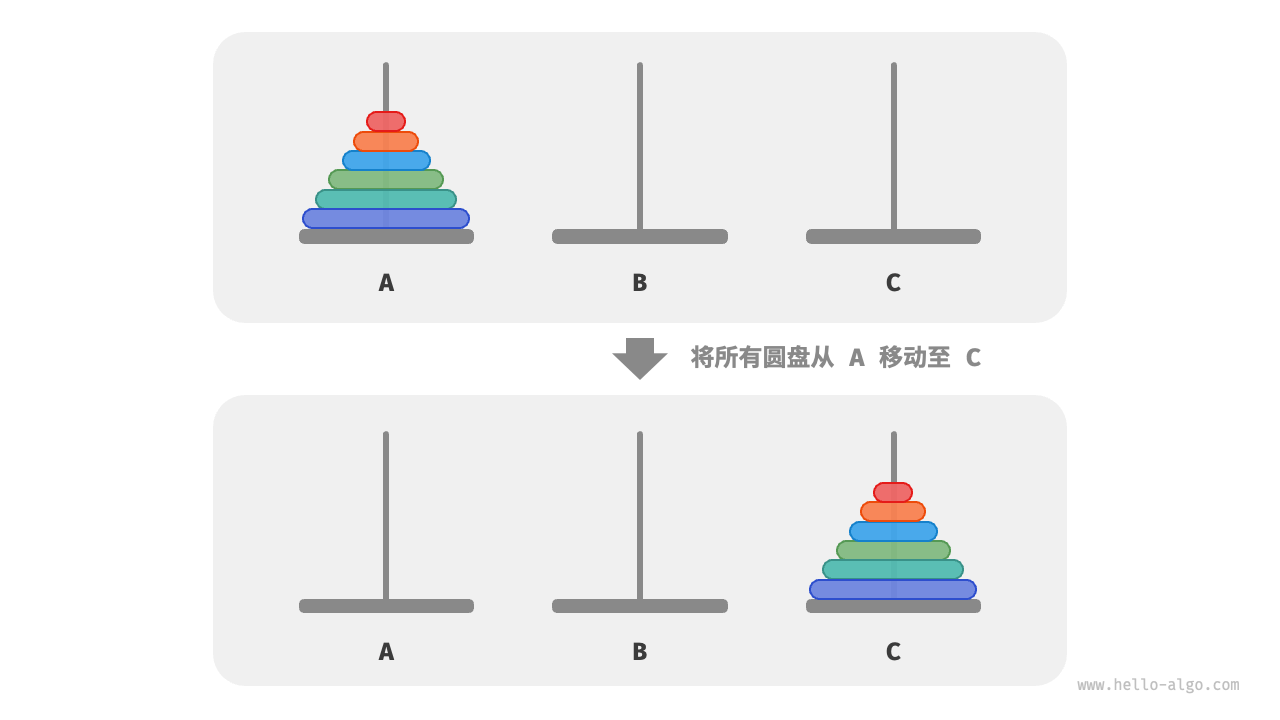
Given three pillars, denoted as A, B, and C. Initially, pillar A is stacked with \(n\) discs, arranged in order from top to bottom from smallest to largest. Our task is to move these \(n\) discs to pillar C, maintaining their original order (as shown below). The following rules must be followed during the disc movement process:

1. A disc can only be picked up from the top of a pillar and placed on top of another pillar.
2. Only one disc can be moved at a time.
3. A smaller disc must always be on top of a larger disc.

Figure 12-10   Example of the Tower of Hanoi

We denote the Tower of Hanoi of size \(i\) as \(f(i)\). For example, \(f(3)\) represents the Tower of Hanoi of moving \(3\) discs from A to C.

1.   Consider the base case

As shown below, for the problem \(f(1)\), i.e., when there is only one disc, we can directly move it from A to C.

<1><2>

Figure 12-11   Solution for a problem of size 1

As shown below, for the problem \(f(2)\), i.e., when there are two discs, since the smaller disc must always be above the larger disc, B is needed to assist in the movement.

1. First, move the smaller disc from A to B.
2. Then move the larger disc from A to C.
3. Finally, move the smaller disc from B to C.

<1><2><3><4>

Figure 12-12   Solution for a problem of size 2

The process of solving the problem \(f(2)\) can be summarized as: moving two discs from A to C with the help of B. Here, C is called the target pillar, and B is called the buffer pillar.

2.   Decomposition of subproblems

For the problem \(f(3)\), i.e., when there are three discs, the situation becomes slightly more complicated.

Since we already know the solutions to \(f(1)\) and \(f(2)\), we can think from a divide-and-conquer perspective and consider the two top discs on A as a unit, performing the steps shown below. This way, the three discs are successfully moved from A to C.

1. Let B be the target pillar and C the buffer pillar, and move the two discs from A to B.
2. Move the remaining disc from A directly to C.
3. Let C be the target pillar and A the buffer pillar, and move the two discs from B to C.

<1><2><3><4>

Figure 12-13   Solution for a problem of size 3

Essentially, we divide the problem \(f(3)\) into two subproblems \(f(2)\) and one subproblem \(f(1)\). By solving these three subproblems in order, the original problem is resolved. This indicates that the subproblems are independent, and their solutions can be merged.

From this, we can summarize the divide-and-conquer strategy for solving the Tower of Hanoi shown in the following image: divide the original problem \(f(n)\) into two subproblems \(f(n-1)\) and one subproblem \(f(1)\), and solve these three subproblems in the following order.

1. Move \(n-1\) discs with the help of C from A to B.
2. Move the remaining one disc directly from A to C.
3. Move \(n-1\) discs with the help of A from B to C.

For these two subproblems \(f(n-1)\), they can be recursively divided in the same manner until the smallest subproblem \(f(1)\) is reached. The solution to \(f(1)\) is already known and requires only one move.

Figure 12-14   Divide and conquer strategy for solving the Tower of Hanoi

3.   Code implementation

In the code, we declare a recursive function dfs(i, src, buf, tar) whose role is to move the \(i\) discs on top of pillar src with the help of buffer pillar buf to the target pillar tar:

PythonC++JavaC#GoSwiftJSTSDartRustCKotlinRubyZig

hanota.py

def move(src: list[int], tar: list[int]):
    """移动一个圆盘"""
    # 从 src 顶部拿出一个圆盘
    pan = src.pop()
    # 将圆盘放入 tar 顶部
    tar.append(pan)

def dfs(i: int, src: list[int], buf: list[int], tar: list[int]):
    """求解汉诺塔问题 f(i)"""
    # 若 src 只剩下一个圆盘，则直接将其移到 tar
    if i == 1:
        move(src, tar)
        return
    # 子问题 f(i-1) ：将 src 顶部 i-1 个圆盘借助 tar 移到 buf
    dfs(i - 1, src, tar, buf)
    # 子问题 f(1) ：将 src 剩余一个圆盘移到 tar
    move(src, tar)
    # 子问题 f(i-1) ：将 buf 顶部 i-1 个圆盘借助 src 移到 tar
    dfs(i - 1, buf, src, tar)

def solve_hanota(A: list[int], B: list[int], C: list[int]):
    """求解汉诺塔问题"""
    n = len(A)
    # 将 A 顶部 n 个圆盘借助 B 移到 C
    dfs(n, A, B, C)

hanota.cpp

/* 移动一个圆盘 */
void move(vector<int> &src, vector<int> &tar) {
    // 从 src 顶部拿出一个圆盘
    int pan = src.back();
    src.pop_back();
    // 将圆盘放入 tar 顶部
    tar.push_back(pan);
}

/* 求解汉诺塔问题 f(i) */
void dfs(int i, vector<int> &src, vector<int> &buf, vector<int> &tar) {
    // 若 src 只剩下一个圆盘，则直接将其移到 tar
    if (i == 1) {
        move(src, tar);
        return;
    }
    // 子问题 f(i-1) ：将 src 顶部 i-1 个圆盘借助 tar 移到 buf
    dfs(i - 1, src, tar, buf);
    // 子问题 f(1) ：将 src 剩余一个圆盘移到 tar
    move(src, tar);
    // 子问题 f(i-1) ：将 buf 顶部 i-1 个圆盘借助 src 移到 tar
    dfs(i - 1, buf, src, tar);
}

/* 求解汉诺塔问题 */
void solveHanota(vector<int> &A, vector<int> &B, vector<int> &C) {
    int n = A.size();
    // 将 A 顶部 n 个圆盘借助 B 移到 C
    dfs(n, A, B, C);
}

hanota.java

/* 移动一个圆盘 */
void move(List<Integer> src, List<Integer> tar) {
    // 从 src 顶部拿出一个圆盘
    Integer pan = src.remove(src.size() - 1);
    // 将圆盘放入 tar 顶部
    tar.add(pan);
}

/* 求解汉诺塔问题 f(i) */
void dfs(int i, List<Integer> src, List<Integer> buf, List<Integer> tar) {
    // 若 src 只剩下一个圆盘，则直接将其移到 tar
    if (i == 1) {
        move(src, tar);
        return;
    }
    // 子问题 f(i-1) ：将 src 顶部 i-1 个圆盘借助 tar 移到 buf
    dfs(i - 1, src, tar, buf);
    // 子问题 f(1) ：将 src 剩余一个圆盘移到 tar
    move(src, tar);
    // 子问题 f(i-1) ：将 buf 顶部 i-1 个圆盘借助 src 移到 tar
    dfs(i - 1, buf, src, tar);
}

/* 求解汉诺塔问题 */
void solveHanota(List<Integer> A, List<Integer> B, List<Integer> C) {
    int n = A.size();
    // 将 A 顶部 n 个圆盘借助 B 移到 C
    dfs(n, A, B, C);
}

hanota.cs

/* 移动一个圆盘 */
void Move(List<int> src, List<int> tar) {
    // 从 src 顶部拿出一个圆盘
    int pan = src[^1];
    src.RemoveAt(src.Count - 1);
    // 将圆盘放入 tar 顶部
    tar.Add(pan);
}

/* 求解汉诺塔问题 f(i) */
void DFS(int i, List<int> src, List<int> buf, List<int> tar) {
    // 若 src 只剩下一个圆盘，则直接将其移到 tar
    if (i == 1) {
        Move(src, tar);
        return;
    }
    // 子问题 f(i-1) ：将 src 顶部 i-1 个圆盘借助 tar 移到 buf
    DFS(i - 1, src, tar, buf);
    // 子问题 f(1) ：将 src 剩余一个圆盘移到 tar
    Move(src, tar);
    // 子问题 f(i-1) ：将 buf 顶部 i-1 个圆盘借助 src 移到 tar
    DFS(i - 1, buf, src, tar);
}

/* 求解汉诺塔问题 */
void SolveHanota(List<int> A, List<int> B, List<int> C) {
    int n = A.Count;
    // 将 A 顶部 n 个圆盘借助 B 移到 C
    DFS(n, A, B, C);
}

hanota.go

/* 移动一个圆盘 */
func move(src, tar *list.List) {
    // 从 src 顶部拿出一个圆盘
    pan := src.Back()
    // 将圆盘放入 tar 顶部
    tar.PushBack(pan.Value)
    // 移除 src 顶部圆盘
    src.Remove(pan)
}

/* 求解汉诺塔问题 f(i) */
func dfsHanota(i int, src, buf, tar *list.List) {
    // 若 src 只剩下一个圆盘，则直接将其移到 tar
    if i == 1 {
        move(src, tar)
        return
    }
    // 子问题 f(i-1) ：将 src 顶部 i-1 个圆盘借助 tar 移到 buf
    dfsHanota(i-1, src, tar, buf)
    // 子问题 f(1) ：将 src 剩余一个圆盘移到 tar
    move(src, tar)
    // 子问题 f(i-1) ：将 buf 顶部 i-1 个圆盘借助 src 移到 tar
    dfsHanota(i-1, buf, src, tar)
}

/* 求解汉诺塔问题 */
func solveHanota(A, B, C *list.List) {
    n := A.Len()
    // 将 A 顶部 n 个圆盘借助 B 移到 C
    dfsHanota(n, A, B, C)
}

hanota.swift

/* 移动一个圆盘 */
func move(src: inout [Int], tar: inout [Int]) {
    // 从 src 顶部拿出一个圆盘
    let pan = src.popLast()!
    // 将圆盘放入 tar 顶部
    tar.append(pan)
}

/* 求解汉诺塔问题 f(i) */
func dfs(i: Int, src: inout [Int], buf: inout [Int], tar: inout [Int]) {
    // 若 src 只剩下一个圆盘，则直接将其移到 tar
    if i == 1 {
        move(src: &src, tar: &tar)
        return
    }
    // 子问题 f(i-1) ：将 src 顶部 i-1 个圆盘借助 tar 移到 buf
    dfs(i: i - 1, src: &src, buf: &tar, tar: &buf)
    // 子问题 f(1) ：将 src 剩余一个圆盘移到 tar
    move(src: &src, tar: &tar)
    // 子问题 f(i-1) ：将 buf 顶部 i-1 个圆盘借助 src 移到 tar
    dfs(i: i - 1, src: &buf, buf: &src, tar: &tar)
}

/* 求解汉诺塔问题 */
func solveHanota(A: inout [Int], B: inout [Int], C: inout [Int]) {
    let n = A.count
    // 列表尾部是柱子顶部
    // 将 src 顶部 n 个圆盘借助 B 移到 C
    dfs(i: n, src: &A, buf: &B, tar: &C)
}

hanota.js

/* 移动一个圆盘 */
function move(src, tar) {
    // 从 src 顶部拿出一个圆盘
    const pan = src.pop();
    // 将圆盘放入 tar 顶部
    tar.push(pan);
}

/* 求解汉诺塔问题 f(i) */
function dfs(i, src, buf, tar) {
    // 若 src 只剩下一个圆盘，则直接将其移到 tar
    if (i === 1) {
        move(src, tar);
        return;
    }
    // 子问题 f(i-1) ：将 src 顶部 i-1 个圆盘借助 tar 移到 buf
    dfs(i - 1, src, tar, buf);
    // 子问题 f(1) ：将 src 剩余一个圆盘移到 tar
    move(src, tar);
    // 子问题 f(i-1) ：将 buf 顶部 i-1 个圆盘借助 src 移到 tar
    dfs(i - 1, buf, src, tar);
}

/* 求解汉诺塔问题 */
function solveHanota(A, B, C) {
    const n = A.length;
    // 将 A 顶部 n 个圆盘借助 B 移到 C
    dfs(n, A, B, C);
}

hanota.ts

/* 移动一个圆盘 */
function move(src: number[], tar: number[]): void {
    // 从 src 顶部拿出一个圆盘
    const pan = src.pop();
    // 将圆盘放入 tar 顶部
    tar.push(pan);
}

/* 求解汉诺塔问题 f(i) */
function dfs(i: number, src: number[], buf: number[], tar: number[]): void {
    // 若 src 只剩下一个圆盘，则直接将其移到 tar
    if (i === 1) {
        move(src, tar);
        return;
    }
    // 子问题 f(i-1) ：将 src 顶部 i-1 个圆盘借助 tar 移到 buf
    dfs(i - 1, src, tar, buf);
    // 子问题 f(1) ：将 src 剩余一个圆盘移到 tar
    move(src, tar);
    // 子问题 f(i-1) ：将 buf 顶部 i-1 个圆盘借助 src 移到 tar
    dfs(i - 1, buf, src, tar);
}

/* 求解汉诺塔问题 */
function solveHanota(A: number[], B: number[], C: number[]): void {
    const n = A.length;
    // 将 A 顶部 n 个圆盘借助 B 移到 C
    dfs(n, A, B, C);
}

hanota.dart

/* 移动一个圆盘 */
void move(List<int> src, List<int> tar) {
  // 从 src 顶部拿出一个圆盘
  int pan = src.removeLast();
  // 将圆盘放入 tar 顶部
  tar.add(pan);
}

/* 求解汉诺塔问题 f(i) */
void dfs(int i, List<int> src, List<int> buf, List<int> tar) {
  // 若 src 只剩下一个圆盘，则直接将其移到 tar
  if (i == 1) {
    move(src, tar);
    return;
  }
  // 子问题 f(i-1) ：将 src 顶部 i-1 个圆盘借助 tar 移到 buf
  dfs(i - 1, src, tar, buf);
  // 子问题 f(1) ：将 src 剩余一个圆盘移到 tar
  move(src, tar);
  // 子问题 f(i-1) ：将 buf 顶部 i-1 个圆盘借助 src 移到 tar
  dfs(i - 1, buf, src, tar);
}

/* 求解汉诺塔问题 */
void solveHanota(List<int> A, List<int> B, List<int> C) {
  int n = A.length;
  // 将 A 顶部 n 个圆盘借助 B 移到 C
  dfs(n, A, B, C);
}

hanota.rs

/* 移动一个圆盘 */
fn move_pan(src: &mut Vec<i32>, tar: &mut Vec<i32>) {
    // 从 src 顶部拿出一个圆盘
    let pan = src.remove(src.len() - 1);
    // 将圆盘放入 tar 顶部
    tar.push(pan);
}

/* 求解汉诺塔问题 f(i) */
fn dfs(i: i32, src: &mut Vec<i32>, buf: &mut Vec<i32>, tar: &mut Vec<i32>) {
    // 若 src 只剩下一个圆盘，则直接将其移到 tar
    if i == 1 {
        move_pan(src, tar);
        return;
    }
    // 子问题 f(i-1) ：将 src 顶部 i-1 个圆盘借助 tar 移到 buf
    dfs(i - 1, src, tar, buf);
    // 子问题 f(1) ：将 src 剩余一个圆盘移到 tar
    move_pan(src, tar);
    // 子问题 f(i-1) ：将 buf 顶部 i-1 个圆盘借助 src 移到 tar
    dfs(i - 1, buf, src, tar);
}

/* 求解汉诺塔问题 */
fn solve_hanota(A: &mut Vec<i32>, B: &mut Vec<i32>, C: &mut Vec<i32>) {
    let n = A.len() as i32;
    // 将 A 顶部 n 个圆盘借助 B 移到 C
    dfs(n, A, B, C);
}

hanota.c

/* 移动一个圆盘 */
void move(int *src, int *srcSize, int *tar, int *tarSize) {
    // 从 src 顶部拿出一个圆盘
    int pan = src[*srcSize - 1];
    src[*srcSize - 1] = 0;
    (*srcSize)--;
    // 将圆盘放入 tar 顶部
    tar[*tarSize] = pan;
    (*tarSize)++;
}

/* 求解汉诺塔问题 f(i) */
void dfs(int i, int *src, int *srcSize, int *buf, int *bufSize, int *tar, int *tarSize) {
    // 若 src 只剩下一个圆盘，则直接将其移到 tar
    if (i == 1) {
        move(src, srcSize, tar, tarSize);
        return;
    }
    // 子问题 f(i-1) ：将 src 顶部 i-1 个圆盘借助 tar 移到 buf
    dfs(i - 1, src, srcSize, tar, tarSize, buf, bufSize);
    // 子问题 f(1) ：将 src 剩余一个圆盘移到 tar
    move(src, srcSize, tar, tarSize);
    // 子问题 f(i-1) ：将 buf 顶部 i-1 个圆盘借助 src 移到 tar
    dfs(i - 1, buf, bufSize, src, srcSize, tar, tarSize);
}

/* 求解汉诺塔问题 */
void solveHanota(int *A, int *ASize, int *B, int *BSize, int *C, int *CSize) {
    // 将 A 顶部 n 个圆盘借助 B 移到 C
    dfs(*ASize, A, ASize, B, BSize, C, CSize);
}

hanota.kt

/* 移动一个圆盘 */
fun move(src: MutableList<Int>, tar: MutableList<Int>) {
    // 从 src 顶部拿出一个圆盘
    val pan = src.removeAt(src.size - 1)
    // 将圆盘放入 tar 顶部
    tar.add(pan)
}

/* 求解汉诺塔问题 f(i) */
fun dfs(i: Int, src: MutableList<Int>, buf: MutableList<Int>, tar: MutableList<Int>) {
    // 若 src 只剩下一个圆盘，则直接将其移到 tar
    if (i == 1) {
        move(src, tar)
        return
    }
    // 子问题 f(i-1) ：将 src 顶部 i-1 个圆盘借助 tar 移到 buf
    dfs(i - 1, src, tar, buf)
    // 子问题 f(1) ：将 src 剩余一个圆盘移到 tar
    move(src, tar)
    // 子问题 f(i-1) ：将 buf 顶部 i-1 个圆盘借助 src 移到 tar
    dfs(i - 1, buf, src, tar)
}

/* 求解汉诺塔问题 */
fun solveHanota(A: MutableList<Int>, B: MutableList<Int>, C: MutableList<Int>) {
    val n = A.size
    // 将 A 顶部 n 个圆盘借助 B 移到 C
    dfs(n, A, B, C)
}

hanota.rb

[class]{}-[func]{move}

[class]{}-[func]{dfs}

[class]{}-[func]{solve_hanota}

hanota.zig

[class]{}-[func]{move}

[class]{}-[func]{dfs}

[class]{}-[func]{solveHanota}

Code Visualization

Full Screen >

As shown below, the Tower of Hanoi forms a recursive tree with a height of \(n\), each node representing a subproblem, corresponding to an open dfs() function, thus the time complexity is \(O(2^n)\), and the space complexity is \(O(n)\).

Figure 12-15   Recursive tree of the Tower of Hanoi

Quote

The Tower of Hanoi originates from an ancient legend. In a temple in ancient India, monks had three tall diamond pillars and \(64\) differently sized golden discs. The monks continuously moved the discs, believing that when the last disc is correctly placed, the world would end.

However, even if the monks moved a disc every second, it would take about \(2^{64} \approx 1.84×10^{19}\) seconds, approximately 585 billion years, far exceeding current estimates of the age of the universe. Thus, if the legend is true, we probably do not need to worry about the world ending.

Feel free to drop your insights, questions or suggestions