13.4 n queens problem¶
Question
According to the rules of chess, a queen can attack pieces in the same row, column, or on a diagonal line. Given \(n\) queens and an \(n \times n\) chessboard, find arrangements where no two queens can attack each other.
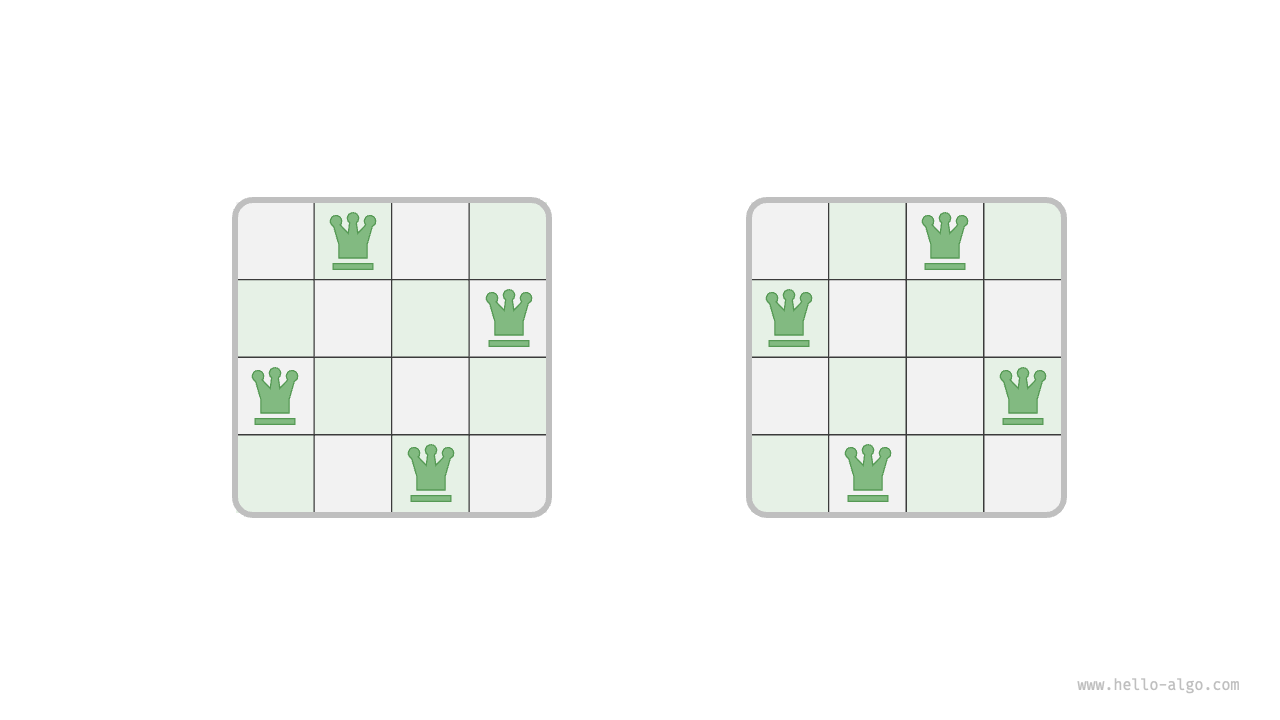
As shown in the Figure 13-15 , when \(n = 4\), there are two solutions. From the perspective of the backtracking algorithm, an \(n \times n\) chessboard has \(n^2\) squares, presenting all possible choices choices. The state of the chessboard state changes continuously as each queen is placed.
Figure 13-15 Solution to the 4 queens problem
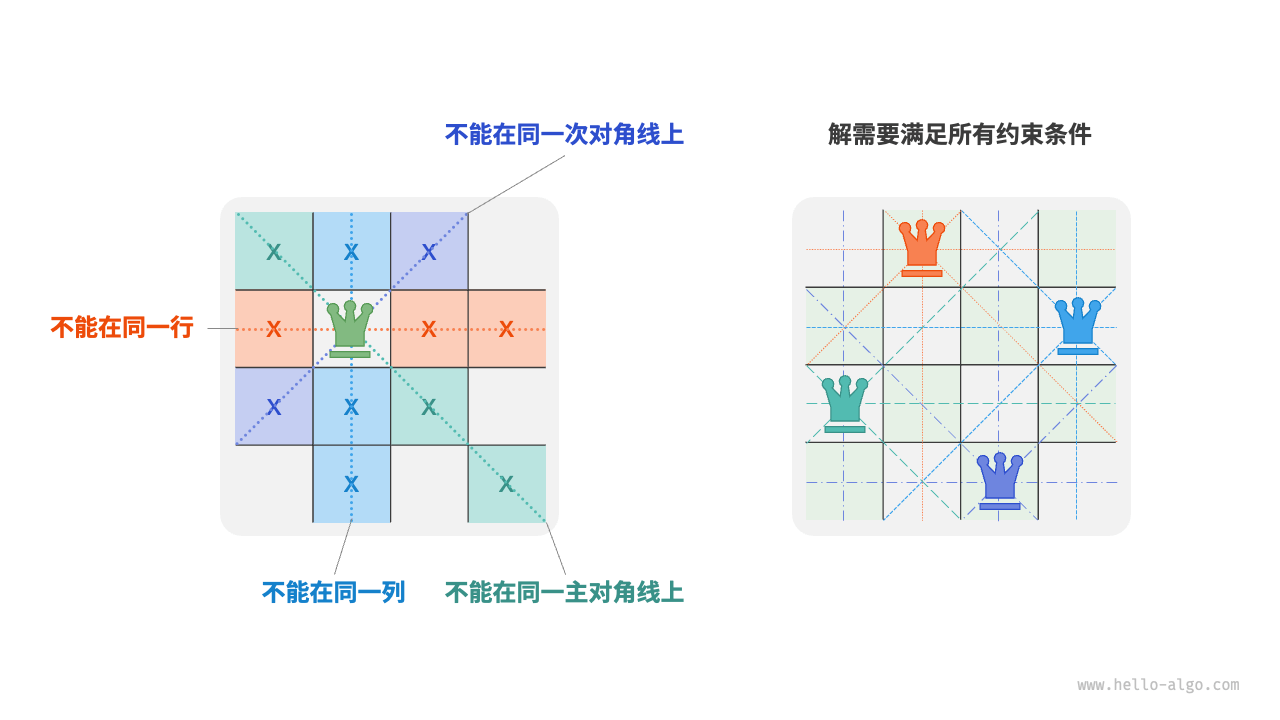
The following image shows the three constraints of this problem: multiple queens cannot be on the same row, column, or diagonal. It is important to note that diagonals are divided into the main diagonal \ and the secondary diagonal /.
Figure 13-16 Constraints of the n queens problem
1. Row-by-row placing strategy¶
As the number of queens equals the number of rows on the chessboard, both being \(n\), it is easy to conclude: each row on the chessboard allows and only allows one queen to be placed.
This means that we can adopt a row-by-row placing strategy: starting from the first row, place one queen per row until the last row is reached.
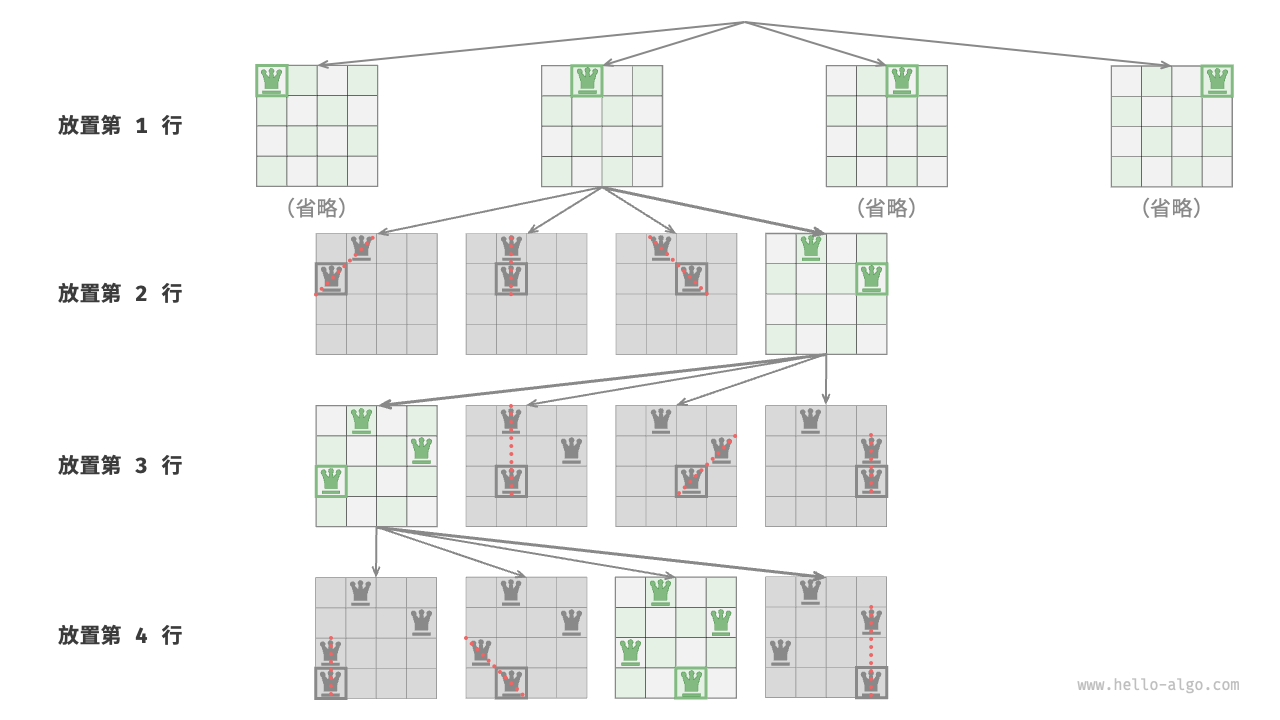
The image below shows the row-by-row placing process for the 4 queens problem. Due to space limitations, the image only expands one search branch of the first row, and prunes any placements that do not meet the column and diagonal constraints.
Figure 13-17 Row-by-row placing strategy
Essentially, the row-by-row placing strategy serves as a pruning function, avoiding all search branches that would place multiple queens in the same row.
2. Column and diagonal pruning¶
To satisfy column constraints, we can use a boolean array cols of length \(n\) to track whether a queen occupies each column. Before each placement decision, cols is used to prune the columns that already have queens, and it is dynamically updated during backtracking.
How about the diagonal constraints? Let the row and column indices of a cell on the chessboard be \((row, col)\). By selecting a specific main diagonal, we notice that the difference \(row - col\) is the same for all cells on that diagonal, meaning that \(row - col\) is a constant value on that diagonal.
Thus, if two cells satisfy \(row_1 - col_1 = row_2 - col_2\), they are definitely on the same main diagonal. Using this pattern, we can utilize the array diags1 shown below to track whether a queen is on any main diagonal.
Similarly, the sum \(row + col\) is a constant value for all cells on a secondary diagonal. We can also use the array diags2 to handle secondary diagonal constraints.
Figure 13-18 Handling column and diagonal constraints
3. Code implementation¶
Please note, in an \(n\)-dimensional matrix, the range of \(row - col\) is \([-n + 1, n - 1]\), and the range of \(row + col\) is \([0, 2n - 2]\), thus the number of both main and secondary diagonals is \(2n - 1\), meaning the length of both arrays diags1 and diags2 is \(2n - 1\).
def backtrack(
row: int,
n: int,
state: list[list[str]],
res: list[list[list[str]]],
cols: list[bool],
diags1: list[bool],
diags2: list[bool],
):
"""回溯算法:n 皇后"""
# 当放置完所有行时,记录解
if row == n:
res.append([list(row) for row in state])
return
# 遍历所有列
for col in range(n):
# 计算该格子对应的主对角线和次对角线
diag1 = row - col + n - 1
diag2 = row + col
# 剪枝:不允许该格子所在列、主对角线、次对角线上存在皇后
if not cols[col] and not diags1[diag1] and not diags2[diag2]:
# 尝试:将皇后放置在该格子
state[row][col] = "Q"
cols[col] = diags1[diag1] = diags2[diag2] = True
# 放置下一行
backtrack(row + 1, n, state, res, cols, diags1, diags2)
# 回退:将该格子恢复为空位
state[row][col] = "#"
cols[col] = diags1[diag1] = diags2[diag2] = False
def n_queens(n: int) -> list[list[list[str]]]:
"""求解 n 皇后"""
# 初始化 n*n 大小的棋盘,其中 'Q' 代表皇后,'#' 代表空位
state = [["#" for _ in range(n)] for _ in range(n)]
cols = [False] * n # 记录列是否有皇后
diags1 = [False] * (2 * n - 1) # 记录主对角线上是否有皇后
diags2 = [False] * (2 * n - 1) # 记录次对角线上是否有皇后
res = []
backtrack(0, n, state, res, cols, diags1, diags2)
return res
/* 回溯算法:n 皇后 */
void backtrack(int row, int n, vector<vector<string>> &state, vector<vector<vector<string>>> &res, vector<bool> &cols,
vector<bool> &diags1, vector<bool> &diags2) {
// 当放置完所有行时,记录解
if (row == n) {
res.push_back(state);
return;
}
// 遍历所有列
for (int col = 0; col < n; col++) {
// 计算该格子对应的主对角线和次对角线
int diag1 = row - col + n - 1;
int diag2 = row + col;
// 剪枝:不允许该格子所在列、主对角线、次对角线上存在皇后
if (!cols[col] && !diags1[diag1] && !diags2[diag2]) {
// 尝试:将皇后放置在该格子
state[row][col] = "Q";
cols[col] = diags1[diag1] = diags2[diag2] = true;
// 放置下一行
backtrack(row + 1, n, state, res, cols, diags1, diags2);
// 回退:将该格子恢复为空位
state[row][col] = "#";
cols[col] = diags1[diag1] = diags2[diag2] = false;
}
}
}
/* 求解 n 皇后 */
vector<vector<vector<string>>> nQueens(int n) {
// 初始化 n*n 大小的棋盘,其中 'Q' 代表皇后,'#' 代表空位
vector<vector<string>> state(n, vector<string>(n, "#"));
vector<bool> cols(n, false); // 记录列是否有皇后
vector<bool> diags1(2 * n - 1, false); // 记录主对角线上是否有皇后
vector<bool> diags2(2 * n - 1, false); // 记录次对角线上是否有皇后
vector<vector<vector<string>>> res;
backtrack(0, n, state, res, cols, diags1, diags2);
return res;
}
/* 回溯算法:n 皇后 */
void backtrack(int row, int n, List<List<String>> state, List<List<List<String>>> res,
boolean[] cols, boolean[] diags1, boolean[] diags2) {
// 当放置完所有行时,记录解
if (row == n) {
List<List<String>> copyState = new ArrayList<>();
for (List<String> sRow : state) {
copyState.add(new ArrayList<>(sRow));
}
res.add(copyState);
return;
}
// 遍历所有列
for (int col = 0; col < n; col++) {
// 计算该格子对应的主对角线和次对角线
int diag1 = row - col + n - 1;
int diag2 = row + col;
// 剪枝:不允许该格子所在列、主对角线、次对角线上存在皇后
if (!cols[col] && !diags1[diag1] && !diags2[diag2]) {
// 尝试:将皇后放置在该格子
state.get(row).set(col, "Q");
cols[col] = diags1[diag1] = diags2[diag2] = true;
// 放置下一行
backtrack(row + 1, n, state, res, cols, diags1, diags2);
// 回退:将该格子恢复为空位
state.get(row).set(col, "#");
cols[col] = diags1[diag1] = diags2[diag2] = false;
}
}
}
/* 求解 n 皇后 */
List<List<List<String>>> nQueens(int n) {
// 初始化 n*n 大小的棋盘,其中 'Q' 代表皇后,'#' 代表空位
List<List<String>> state = new ArrayList<>();
for (int i = 0; i < n; i++) {
List<String> row = new ArrayList<>();
for (int j = 0; j < n; j++) {
row.add("#");
}
state.add(row);
}
boolean[] cols = new boolean[n]; // 记录列是否有皇后
boolean[] diags1 = new boolean[2 * n - 1]; // 记录主对角线上是否有皇后
boolean[] diags2 = new boolean[2 * n - 1]; // 记录次对角线上是否有皇后
List<List<List<String>>> res = new ArrayList<>();
backtrack(0, n, state, res, cols, diags1, diags2);
return res;
}
/* 回溯算法:n 皇后 */
void Backtrack(int row, int n, List<List<string>> state, List<List<List<string>>> res,
bool[] cols, bool[] diags1, bool[] diags2) {
// 当放置完所有行时,记录解
if (row == n) {
List<List<string>> copyState = [];
foreach (List<string> sRow in state) {
copyState.Add(new List<string>(sRow));
}
res.Add(copyState);
return;
}
// 遍历所有列
for (int col = 0; col < n; col++) {
// 计算该格子对应的主对角线和次对角线
int diag1 = row - col + n - 1;
int diag2 = row + col;
// 剪枝:不允许该格子所在列、主对角线、次对角线上存在皇后
if (!cols[col] && !diags1[diag1] && !diags2[diag2]) {
// 尝试:将皇后放置在该格子
state[row][col] = "Q";
cols[col] = diags1[diag1] = diags2[diag2] = true;
// 放置下一行
Backtrack(row + 1, n, state, res, cols, diags1, diags2);
// 回退:将该格子恢复为空位
state[row][col] = "#";
cols[col] = diags1[diag1] = diags2[diag2] = false;
}
}
}
/* 求解 n 皇后 */
List<List<List<string>>> NQueens(int n) {
// 初始化 n*n 大小的棋盘,其中 'Q' 代表皇后,'#' 代表空位
List<List<string>> state = [];
for (int i = 0; i < n; i++) {
List<string> row = [];
for (int j = 0; j < n; j++) {
row.Add("#");
}
state.Add(row);
}
bool[] cols = new bool[n]; // 记录列是否有皇后
bool[] diags1 = new bool[2 * n - 1]; // 记录主对角线上是否有皇后
bool[] diags2 = new bool[2 * n - 1]; // 记录次对角线上是否有皇后
List<List<List<string>>> res = [];
Backtrack(0, n, state, res, cols, diags1, diags2);
return res;
}
/* 回溯算法:n 皇后 */
func backtrack(row, n int, state *[][]string, res *[][][]string, cols, diags1, diags2 *[]bool) {
// 当放置完所有行时,记录解
if row == n {
newState := make([][]string, len(*state))
for i, _ := range newState {
newState[i] = make([]string, len((*state)[0]))
copy(newState[i], (*state)[i])
}
*res = append(*res, newState)
}
// 遍历所有列
for col := 0; col < n; col++ {
// 计算该格子对应的主对角线和次对角线
diag1 := row - col + n - 1
diag2 := row + col
// 剪枝:不允许该格子所在列、主对角线、次对角线上存在皇后
if !(*cols)[col] && !(*diags1)[diag1] && !(*diags2)[diag2] {
// 尝试:将皇后放置在该格子
(*state)[row][col] = "Q"
(*cols)[col], (*diags1)[diag1], (*diags2)[diag2] = true, true, true
// 放置下一行
backtrack(row+1, n, state, res, cols, diags1, diags2)
// 回退:将该格子恢复为空位
(*state)[row][col] = "#"
(*cols)[col], (*diags1)[diag1], (*diags2)[diag2] = false, false, false
}
}
}
/* 求解 n 皇后 */
func nQueens(n int) [][][]string {
// 初始化 n*n 大小的棋盘,其中 'Q' 代表皇后,'#' 代表空位
state := make([][]string, n)
for i := 0; i < n; i++ {
row := make([]string, n)
for i := 0; i < n; i++ {
row[i] = "#"
}
state[i] = row
}
// 记录列是否有皇后
cols := make([]bool, n)
diags1 := make([]bool, 2*n-1)
diags2 := make([]bool, 2*n-1)
res := make([][][]string, 0)
backtrack(0, n, &state, &res, &cols, &diags1, &diags2)
return res
}
/* 回溯算法:n 皇后 */
func backtrack(row: Int, n: Int, state: inout [[String]], res: inout [[[String]]], cols: inout [Bool], diags1: inout [Bool], diags2: inout [Bool]) {
// 当放置完所有行时,记录解
if row == n {
res.append(state)
return
}
// 遍历所有列
for col in 0 ..< n {
// 计算该格子对应的主对角线和次对角线
let diag1 = row - col + n - 1
let diag2 = row + col
// 剪枝:不允许该格子所在列、主对角线、次对角线上存在皇后
if !cols[col] && !diags1[diag1] && !diags2[diag2] {
// 尝试:将皇后放置在该格子
state[row][col] = "Q"
cols[col] = true
diags1[diag1] = true
diags2[diag2] = true
// 放置下一行
backtrack(row: row + 1, n: n, state: &state, res: &res, cols: &cols, diags1: &diags1, diags2: &diags2)
// 回退:将该格子恢复为空位
state[row][col] = "#"
cols[col] = false
diags1[diag1] = false
diags2[diag2] = false
}
}
}
/* 求解 n 皇后 */
func nQueens(n: Int) -> [[[String]]] {
// 初始化 n*n 大小的棋盘,其中 'Q' 代表皇后,'#' 代表空位
var state = Array(repeating: Array(repeating: "#", count: n), count: n)
var cols = Array(repeating: false, count: n) // 记录列是否有皇后
var diags1 = Array(repeating: false, count: 2 * n - 1) // 记录主对角线上是否有皇后
var diags2 = Array(repeating: false, count: 2 * n - 1) // 记录次对角线上是否有皇后
var res: [[[String]]] = []
backtrack(row: 0, n: n, state: &state, res: &res, cols: &cols, diags1: &diags1, diags2: &diags2)
return res
}
/* 回溯算法:n 皇后 */
function backtrack(row, n, state, res, cols, diags1, diags2) {
// 当放置完所有行时,记录解
if (row === n) {
res.push(state.map((row) => row.slice()));
return;
}
// 遍历所有列
for (let col = 0; col < n; col++) {
// 计算该格子对应的主对角线和次对角线
const diag1 = row - col + n - 1;
const diag2 = row + col;
// 剪枝:不允许该格子所在列、主对角线、次对角线上存在皇后
if (!cols[col] && !diags1[diag1] && !diags2[diag2]) {
// 尝试:将皇后放置在该格子
state[row][col] = 'Q';
cols[col] = diags1[diag1] = diags2[diag2] = true;
// 放置下一行
backtrack(row + 1, n, state, res, cols, diags1, diags2);
// 回退:将该格子恢复为空位
state[row][col] = '#';
cols[col] = diags1[diag1] = diags2[diag2] = false;
}
}
}
/* 求解 n 皇后 */
function nQueens(n) {
// 初始化 n*n 大小的棋盘,其中 'Q' 代表皇后,'#' 代表空位
const state = Array.from({ length: n }, () => Array(n).fill('#'));
const cols = Array(n).fill(false); // 记录列是否有皇后
const diags1 = Array(2 * n - 1).fill(false); // 记录主对角线上是否有皇后
const diags2 = Array(2 * n - 1).fill(false); // 记录次对角线上是否有皇后
const res = [];
backtrack(0, n, state, res, cols, diags1, diags2);
return res;
}
/* 回溯算法:n 皇后 */
function backtrack(
row: number,
n: number,
state: string[][],
res: string[][][],
cols: boolean[],
diags1: boolean[],
diags2: boolean[]
): void {
// 当放置完所有行时,记录解
if (row === n) {
res.push(state.map((row) => row.slice()));
return;
}
// 遍历所有列
for (let col = 0; col < n; col++) {
// 计算该格子对应的主对角线和次对角线
const diag1 = row - col + n - 1;
const diag2 = row + col;
// 剪枝:不允许该格子所在列、主对角线、次对角线上存在皇后
if (!cols[col] && !diags1[diag1] && !diags2[diag2]) {
// 尝试:将皇后放置在该格子
state[row][col] = 'Q';
cols[col] = diags1[diag1] = diags2[diag2] = true;
// 放置下一行
backtrack(row + 1, n, state, res, cols, diags1, diags2);
// 回退:将该格子恢复为空位
state[row][col] = '#';
cols[col] = diags1[diag1] = diags2[diag2] = false;
}
}
}
/* 求解 n 皇后 */
function nQueens(n: number): string[][][] {
// 初始化 n*n 大小的棋盘,其中 'Q' 代表皇后,'#' 代表空位
const state = Array.from({ length: n }, () => Array(n).fill('#'));
const cols = Array(n).fill(false); // 记录列是否有皇后
const diags1 = Array(2 * n - 1).fill(false); // 记录主对角线上是否有皇后
const diags2 = Array(2 * n - 1).fill(false); // 记录次对角线上是否有皇后
const res: string[][][] = [];
backtrack(0, n, state, res, cols, diags1, diags2);
return res;
}
/* 回溯算法:n 皇后 */
void backtrack(
int row,
int n,
List<List<String>> state,
List<List<List<String>>> res,
List<bool> cols,
List<bool> diags1,
List<bool> diags2,
) {
// 当放置完所有行时,记录解
if (row == n) {
List<List<String>> copyState = [];
for (List<String> sRow in state) {
copyState.add(List.from(sRow));
}
res.add(copyState);
return;
}
// 遍历所有列
for (int col = 0; col < n; col++) {
// 计算该格子对应的主对角线和次对角线
int diag1 = row - col + n - 1;
int diag2 = row + col;
// 剪枝:不允许该格子所在列、主对角线、次对角线上存在皇后
if (!cols[col] && !diags1[diag1] && !diags2[diag2]) {
// 尝试:将皇后放置在该格子
state[row][col] = "Q";
cols[col] = true;
diags1[diag1] = true;
diags2[diag2] = true;
// 放置下一行
backtrack(row + 1, n, state, res, cols, diags1, diags2);
// 回退:将该格子恢复为空位
state[row][col] = "#";
cols[col] = false;
diags1[diag1] = false;
diags2[diag2] = false;
}
}
}
/* 求解 n 皇后 */
List<List<List<String>>> nQueens(int n) {
// 初始化 n*n 大小的棋盘,其中 'Q' 代表皇后,'#' 代表空位
List<List<String>> state = List.generate(n, (index) => List.filled(n, "#"));
List<bool> cols = List.filled(n, false); // 记录列是否有皇后
List<bool> diags1 = List.filled(2 * n - 1, false); // 记录主对角线上是否有皇后
List<bool> diags2 = List.filled(2 * n - 1, false); // 记录次对角线上是否有皇后
List<List<List<String>>> res = [];
backtrack(0, n, state, res, cols, diags1, diags2);
return res;
}
/* 回溯算法:n 皇后 */
fn backtrack(
row: usize,
n: usize,
state: &mut Vec<Vec<String>>,
res: &mut Vec<Vec<Vec<String>>>,
cols: &mut [bool],
diags1: &mut [bool],
diags2: &mut [bool],
) {
// 当放置完所有行时,记录解
if row == n {
let mut copy_state: Vec<Vec<String>> = Vec::new();
for s_row in state.clone() {
copy_state.push(s_row);
}
res.push(copy_state);
return;
}
// 遍历所有列
for col in 0..n {
// 计算该格子对应的主对角线和次对角线
let diag1 = row + n - 1 - col;
let diag2 = row + col;
// 剪枝:不允许该格子所在列、主对角线、次对角线上存在皇后
if !cols[col] && !diags1[diag1] && !diags2[diag2] {
// 尝试:将皇后放置在该格子
state.get_mut(row).unwrap()[col] = "Q".into();
(cols[col], diags1[diag1], diags2[diag2]) = (true, true, true);
// 放置下一行
backtrack(row + 1, n, state, res, cols, diags1, diags2);
// 回退:将该格子恢复为空位
state.get_mut(row).unwrap()[col] = "#".into();
(cols[col], diags1[diag1], diags2[diag2]) = (false, false, false);
}
}
}
/* 求解 n 皇后 */
fn n_queens(n: usize) -> Vec<Vec<Vec<String>>> {
// 初始化 n*n 大小的棋盘,其中 'Q' 代表皇后,'#' 代表空位
let mut state: Vec<Vec<String>> = Vec::new();
for _ in 0..n {
let mut row: Vec<String> = Vec::new();
for _ in 0..n {
row.push("#".into());
}
state.push(row);
}
let mut cols = vec![false; n]; // 记录列是否有皇后
let mut diags1 = vec![false; 2 * n - 1]; // 记录主对角线上是否有皇后
let mut diags2 = vec![false; 2 * n - 1]; // 记录次对角线上是否有皇后
let mut res: Vec<Vec<Vec<String>>> = Vec::new();
backtrack(
0,
n,
&mut state,
&mut res,
&mut cols,
&mut diags1,
&mut diags2,
);
res
}
/* 回溯算法:n 皇后 */
void backtrack(int row, int n, char state[MAX_SIZE][MAX_SIZE], char ***res, int *resSize, bool cols[MAX_SIZE],
bool diags1[2 * MAX_SIZE - 1], bool diags2[2 * MAX_SIZE - 1]) {
// 当放置完所有行时,记录解
if (row == n) {
res[*resSize] = (char **)malloc(sizeof(char *) * n);
for (int i = 0; i < n; ++i) {
res[*resSize][i] = (char *)malloc(sizeof(char) * (n + 1));
strcpy(res[*resSize][i], state[i]);
}
(*resSize)++;
return;
}
// 遍历所有列
for (int col = 0; col < n; col++) {
// 计算该格子对应的主对角线和次对角线
int diag1 = row - col + n - 1;
int diag2 = row + col;
// 剪枝:不允许该格子所在列、主对角线、次对角线上存在皇后
if (!cols[col] && !diags1[diag1] && !diags2[diag2]) {
// 尝试:将皇后放置在该格子
state[row][col] = 'Q';
cols[col] = diags1[diag1] = diags2[diag2] = true;
// 放置下一行
backtrack(row + 1, n, state, res, resSize, cols, diags1, diags2);
// 回退:将该格子恢复为空位
state[row][col] = '#';
cols[col] = diags1[diag1] = diags2[diag2] = false;
}
}
}
/* 求解 n 皇后 */
char ***nQueens(int n, int *returnSize) {
char state[MAX_SIZE][MAX_SIZE];
// 初始化 n*n 大小的棋盘,其中 'Q' 代表皇后,'#' 代表空位
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
state[i][j] = '#';
}
state[i][n] = '\0';
}
bool cols[MAX_SIZE] = {false}; // 记录列是否有皇后
bool diags1[2 * MAX_SIZE - 1] = {false}; // 记录主对角线上是否有皇后
bool diags2[2 * MAX_SIZE - 1] = {false}; // 记录次对角线上是否有皇后
char ***res = (char ***)malloc(sizeof(char **) * MAX_SIZE);
*returnSize = 0;
backtrack(0, n, state, res, returnSize, cols, diags1, diags2);
return res;
}
/* 回溯算法:n 皇后 */
fun backtrack(
row: Int,
n: Int,
state: MutableList<MutableList<String>>,
res: MutableList<MutableList<MutableList<String>>?>,
cols: BooleanArray,
diags1: BooleanArray,
diags2: BooleanArray
) {
// 当放置完所有行时,记录解
if (row == n) {
val copyState = mutableListOf<MutableList<String>>()
for (sRow in state) {
copyState.add(sRow.toMutableList())
}
res.add(copyState)
return
}
// 遍历所有列
for (col in 0..<n) {
// 计算该格子对应的主对角线和次对角线
val diag1 = row - col + n - 1
val diag2 = row + col
// 剪枝:不允许该格子所在列、主对角线、次对角线上存在皇后
if (!cols[col] && !diags1[diag1] && !diags2[diag2]) {
// 尝试:将皇后放置在该格子
state[row][col] = "Q"
diags2[diag2] = true
diags1[diag1] = diags2[diag2]
cols[col] = diags1[diag1]
// 放置下一行
backtrack(row + 1, n, state, res, cols, diags1, diags2)
// 回退:将该格子恢复为空位
state[row][col] = "#"
diags2[diag2] = false
diags1[diag1] = diags2[diag2]
cols[col] = diags1[diag1]
}
}
}
/* 求解 n 皇后 */
fun nQueens(n: Int): MutableList<MutableList<MutableList<String>>?> {
// 初始化 n*n 大小的棋盘,其中 'Q' 代表皇后,'#' 代表空位
val state = mutableListOf<MutableList<String>>()
for (i in 0..<n) {
val row = mutableListOf<String>()
for (j in 0..<n) {
row.add("#")
}
state.add(row)
}
val cols = BooleanArray(n) // 记录列是否有皇后
val diags1 = BooleanArray(2 * n - 1) // 记录主对角线上是否有皇后
val diags2 = BooleanArray(2 * n - 1) // 记录次对角线上是否有皇后
val res = mutableListOf<MutableList<MutableList<String>>?>()
backtrack(0, n, state, res, cols, diags1, diags2)
return res
}
Code Visualization
Placing \(n\) queens row-by-row, considering column constraints, from the first row to the last row there are \(n\), \(n-1\), \(\dots\), \(2\), \(1\) choices, using \(O(n!)\) time. When recording a solution, it is necessary to copy the matrix state and add it to res, with the copying operation using \(O(n^2)\) time. Therefore, the overall time complexity is \(O(n! \cdot n^2)\). In practice, pruning based on diagonal constraints can significantly reduce the search space, thus often the search efficiency is better than the above time complexity.
Array state uses \(O(n^2)\) space, and arrays cols, diags1, and diags2 each use \(O(n)\) space. The maximum recursion depth is \(n\), using \(O(n)\) stack space. Therefore, the space complexity is \(O(n^2)\).