12.3. 子集和问题¶

Question

给定一个正整数数组 nums 和一个目标正整数 target ，请找出所有可能的组合，使得组合中的元素和等于 target 。给定数组无重复元素，每个元素可以被选取多次。请以列表形式返回这些组合，列表中不应包含重复组合。

例如，输入集合 \(\{3, 4, 5\}\) 和目标整数 \(9\) ，由于集合中的数字可以被重复选取，因此解为 \(\{3, 3, 3\}, \{4, 5\}\) 。请注意，子集是不区分元素顺序的，例如 \(\{4, 5\}\) 和 \(\{5, 4\}\) 是同一个子集。

12.3.1. 从全排列引出解法¶

类似于上节全排列问题的解法，我们可以把子集的生成过程想象成一系列选择的结果，并在选择过程中实时更新“元素和”，当元素和等于 target 时，就将子集记录至结果列表。

而与全排列问题不同的是，本题允许重复选取同一元素，因此无需借助 selected 布尔列表来记录元素是否已被选择。我们可以对全排列代码进行小幅修改，初步得到解题代码。

JavaC++PythonGoJavaScriptTypeScriptCC#SwiftZigDart

subset_sum_i_naive.java

/* 回溯算法：子集和 I */
void backtrack(List<Integer> state, int target, int total, int[] choices, List<List<Integer>> res) {
    // 子集和等于 target 时，记录解
    if (total == target) {
        res.add(new ArrayList<>(state));
        return;
    }
    // 遍历所有选择
    for (int i = 0; i < choices.length; i++) {
        // 剪枝：若子集和超过 target ，则跳过该选择
        if (total + choices[i] > target) {
            continue;
        }
        // 尝试：做出选择，更新元素和 total
        state.add(choices[i]);
        // 进行下一轮选择
        backtrack(state, target, total + choices[i], choices, res);
        // 回退：撤销选择，恢复到之前的状态
        state.remove(state.size() - 1);
    }
}

/* 求解子集和 I（包含重复子集） */
List<List<Integer>> subsetSumINaive(int[] nums, int target) {
    List<Integer> state = new ArrayList<>(); // 状态（子集）
    int total = 0; // 子集和
    List<List<Integer>> res = new ArrayList<>(); // 结果列表（子集列表）
    backtrack(state, target, total, nums, res);
    return res;
}

subset_sum_i_naive.cpp

/* 回溯算法：子集和 I */
void backtrack(vector<int> &state, int target, int total, vector<int> &choices, vector<vector<int>> &res) {
    // 子集和等于 target 时，记录解
    if (total == target) {
        res.push_back(state);
        return;
    }
    // 遍历所有选择
    for (size_t i = 0; i < choices.size(); i++) {
        // 剪枝：若子集和超过 target ，则跳过该选择
        if (total + choices[i] > target) {
            continue;
        }
        // 尝试：做出选择，更新元素和 total
        state.push_back(choices[i]);
        // 进行下一轮选择
        backtrack(state, target, total + choices[i], choices, res);
        // 回退：撤销选择，恢复到之前的状态
        state.pop_back();
    }
}

/* 求解子集和 I（包含重复子集） */
vector<vector<int>> subsetSumINaive(vector<int> &nums, int target) {
    vector<int> state;       // 状态（子集）
    int total = 0;           // 子集和
    vector<vector<int>> res; // 结果列表（子集列表）
    backtrack(state, target, total, nums, res);
    return res;
}

subset_sum_i_naive.py

def backtrack(
    state: list[int],
    target: int,
    total: int,
    choices: list[int],
    res: list[list[int]],
):
    """回溯算法：子集和 I"""
    # 子集和等于 target 时，记录解
    if total == target:
        res.append(list(state))
        return
    # 遍历所有选择
    for i in range(len(choices)):
        # 剪枝：若子集和超过 target ，则跳过该选择
        if total + choices[i] > target:
            continue
        # 尝试：做出选择，更新元素和 total
        state.append(choices[i])
        # 进行下一轮选择
        backtrack(state, target, total + choices[i], choices, res)
        # 回退：撤销选择，恢复到之前的状态
        state.pop()

def subset_sum_i_naive(nums: list[int], target: int) -> list[list[int]]:
    """求解子集和 I（包含重复子集）"""
    state = []  # 状态（子集）
    total = 0  # 子集和
    res = []  # 结果列表（子集列表）
    backtrack(state, target, total, nums, res)
    return res

subset_sum_i_naive.go

[class]{}-[func]{backtrackINaive}

/* 求解子集和 I（包含重复子集） */
func subsetSumINaive(nums []int, target int) [][]int {
    s := subset{}
    state := make([]int, 0) // 状态（子集）
    total := 0              // 子集和
    res := make([][]int, 0) // 结果列表（子集列表）
    s.backtrack(total, target, &state, &nums, &res)
    return res
}

subset_sum_i_naive.js

[class]{}-[func]{backtrack}

[class]{}-[func]{subsetSumINaive}

subset_sum_i_naive.ts

[class]{}-[func]{backtrack}

[class]{}-[func]{subsetSumINaive}

subset_sum_i_naive.c

[class]{}-[func]{backtrack}

[class]{}-[func]{subsetSumINaive}

subset_sum_i_naive.cs

/* 回溯算法：子集和 I */
void backtrack(List<int> state, int target, int total, int[] choices, List<List<int>> res) {
    // 子集和等于 target 时，记录解
    if (total == target) {
        res.Add(new List<int>(state));
        return;
    }
    // 遍历所有选择
    for (int i = 0; i < choices.Length; i++) {
        // 剪枝：若子集和超过 target ，则跳过该选择
        if (total + choices[i] > target) {
            continue;
        }
        // 尝试：做出选择，更新元素和 total
        state.Add(choices[i]);
        // 进行下一轮选择
        backtrack(state, target, total + choices[i], choices, res);
        // 回退：撤销选择，恢复到之前的状态
        state.RemoveAt(state.Count - 1);
    }
}

/* 求解子集和 I（包含重复子集） */
List<List<int>> subsetSumINaive(int[] nums, int target) {
    List<int> state = new List<int>(); // 状态（子集）
    int total = 0; // 子集和
    List<List<int>> res = new List<List<int>>(); // 结果列表（子集列表）
    backtrack(state, target, total, nums, res);
    return res;
}

subset_sum_i_naive.swift

[class]{}-[func]{backtrack}

[class]{}-[func]{subsetSumINaive}

subset_sum_i_naive.zig

[class]{}-[func]{backtrack}

[class]{}-[func]{subsetSumINaive}

subset_sum_i_naive.dart

[class]{}-[func]{backtrack}

[class]{}-[func]{subsetSumINaive}

向以上代码输入数组 \([3, 4, 5]\) 和目标元素 \(9\) ，输出结果为 \([3, 3, 3], [4, 5], [5, 4]\) 。虽然成功找出了所有和为 \(9\) 的子集，但其中存在重复的子集 \([4, 5]\) 和 \([5, 4]\) 。这是因为搜索过程是区分选择顺序的，如下图所示，先选 \(4\) 后选 \(5\) 与先选 \(5\) 后选 \(4\) 是两种不同的情况。

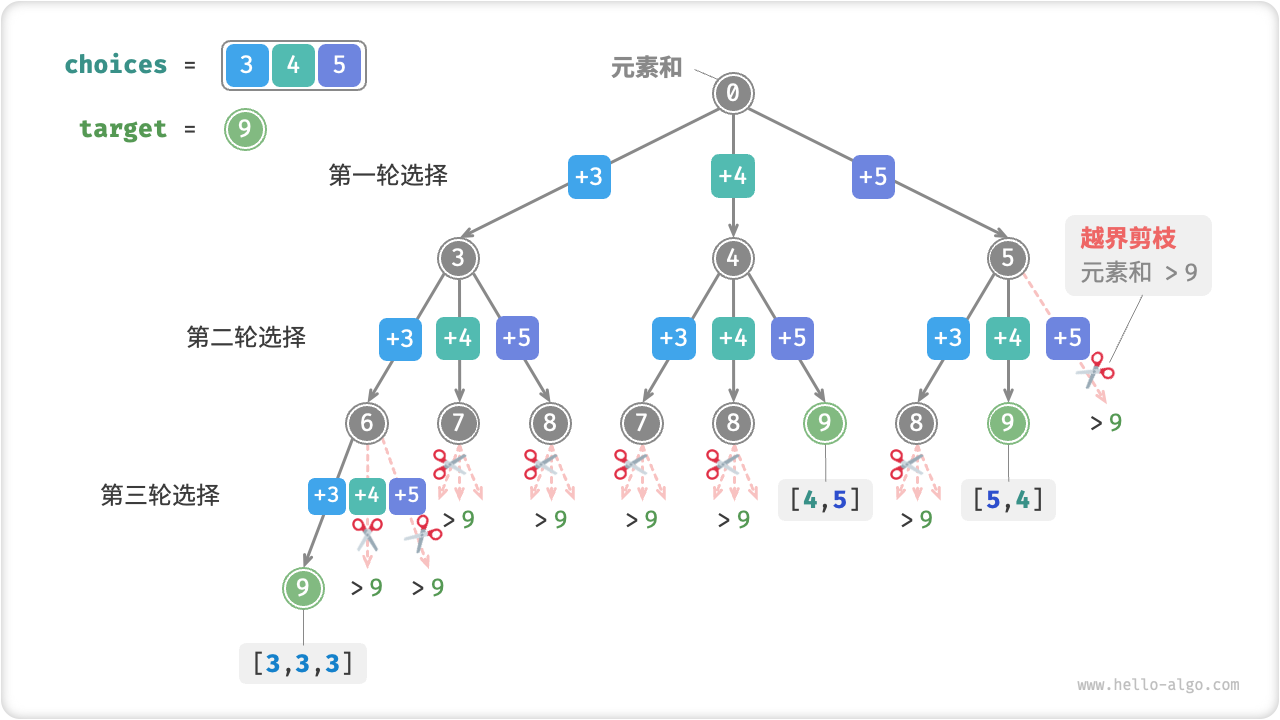
子集搜索与越界剪枝

Fig. 子集搜索与越界剪枝

12.3.2. 重复子集剪枝¶

为了去除重复子集，一种直接的思路是对结果列表进行去重。但这个方法效率很低，因为：

当数组元素较多，尤其是当 target 较大时，搜索过程会产生大量的重复子集。
比较子集（数组）的异同是很耗时的，需要先排序数组，再比较数组中每个元素的异同。

为了达到最佳效率，我们希望在搜索过程中通过剪枝进行去重。观察下图，重复子集是在以不同顺序选择数组元素时产生的，具体来看：

第一轮和第二轮分别选择 \(3\) , \(4\) ，会生成包含这两个元素的所有子集，记为 \([3, 4, \cdots]\) 。
若第一轮选择 \(4\) ，则第二轮应该跳过 \(3\) ，因为该选择产生的子集 \([4, 3, \cdots]\) 和 1. 中提到的子集完全重复。
同理，若第一轮选择 \(5\) ，则第二轮应该跳过 \(3\) 和 \(4\) ，因为子集 \([5, 3, \cdots]\) 和子集 \([5, 4, \cdots]\) 和之前的子集重复。

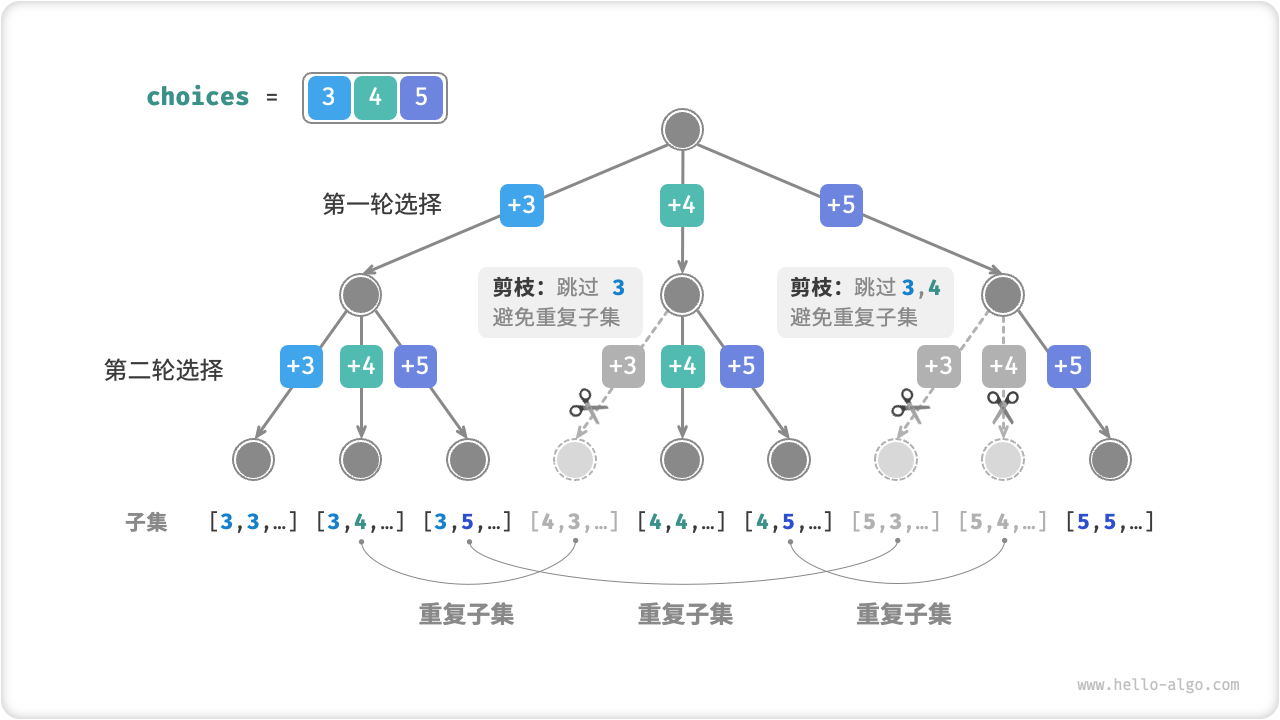
不同选择顺序导致的重复子集

Fig. 不同选择顺序导致的重复子集

总结来看，给定输入数组 \([x_1, x_2, \cdots, x_n]\) ，设搜索过程中的选择序列为 \([x_{i_1}, x_{i_2}, \cdots , x_{i_m}]\) ，则该选择序列需要满足 \(i_1 \leq i_2 \leq \cdots \leq i_m\) 。不满足该条件的选择序列都是重复子集。

为实现该剪枝，我们初始化变量 start ，用于指示遍历起点。当做出选择 \(x_{i}\) 后，设定下一轮从索引 \(i\) 开始遍历，从而完成子集去重。

除此之外，我们还对代码进行了两项优化。首先，我们在开启搜索前将数组 nums 排序，在搜索过程中，当子集和超过 target 时直接结束循环，因为后边的元素更大，其子集和都一定会超过 target 。其次，我们通过在 target 上执行减法来统计元素和，当 target 等于 \(0\) 时记录解，省去了元素和变量 total 。

JavaC++PythonGoJavaScriptTypeScriptCC#SwiftZigDart

subset_sum_i.java

/* 回溯算法：子集和 I */
void backtrack(List<Integer> state, int target, int[] choices, int start, List<List<Integer>> res) {
    // 子集和等于 target 时，记录解
    if (target == 0) {
        res.add(new ArrayList<>(state));
        return;
    }
    // 遍历所有选择
    // 剪枝二：从 start 开始遍历，避免生成重复子集
    for (int i = start; i < choices.length; i++) {
        // 剪枝一：若子集和超过 target ，则直接结束循环
        // 这是因为数组已排序，后边元素更大，子集和一定超过 target
        if (target - choices[i] < 0) {
            break;
        }
        // 尝试：做出选择，更新 target, start
        state.add(choices[i]);
        // 进行下一轮选择
        backtrack(state, target - choices[i], choices, i, res);
        // 回退：撤销选择，恢复到之前的状态
        state.remove(state.size() - 1);
    }
}

/* 求解子集和 I */
List<List<Integer>> subsetSumI(int[] nums, int target) {
    List<Integer> state = new ArrayList<>(); // 状态（子集）
    Arrays.sort(nums); // 对 nums 进行排序
    int start = 0; // 遍历起始点
    List<List<Integer>> res = new ArrayList<>(); // 结果列表（子集列表）
    backtrack(state, target, nums, start, res);
    return res;
}

subset_sum_i.cpp

/* 回溯算法：子集和 I */
void backtrack(vector<int> &state, int target, vector<int> &choices, int start, vector<vector<int>> &res) {
    // 子集和等于 target 时，记录解
    if (target == 0) {
        res.push_back(state);
        return;
    }
    // 遍历所有选择
    // 剪枝二：从 start 开始遍历，避免生成重复子集
    for (int i = start; i < choices.size(); i++) {
        // 剪枝一：若子集和超过 target ，则直接结束循环
        // 这是因为数组已排序，后边元素更大，子集和一定超过 target
        if (target - choices[i] < 0) {
            break;
        }
        // 尝试：做出选择，更新 target, start
        state.push_back(choices[i]);
        // 进行下一轮选择
        backtrack(state, target - choices[i], choices, i, res);
        // 回退：撤销选择，恢复到之前的状态
        state.pop_back();
    }
}

/* 求解子集和 I */
vector<vector<int>> subsetSumI(vector<int> &nums, int target) {
    vector<int> state;              // 状态（子集）
    sort(nums.begin(), nums.end()); // 对 nums 进行排序
    int start = 0;                  // 遍历起始点
    vector<vector<int>> res;        // 结果列表（子集列表）
    backtrack(state, target, nums, start, res);
    return res;
}

subset_sum_i.py

def backtrack(
    state: list[int], target: int, choices: list[int], start: int, res: list[list[int]]
):
    """回溯算法：子集和 I"""
    # 子集和等于 target 时，记录解
    if target == 0:
        res.append(list(state))
        return
    # 遍历所有选择
    # 剪枝二：从 start 开始遍历，避免生成重复子集
    for i in range(start, len(choices)):
        # 剪枝一：若子集和超过 target ，则直接结束循环
        # 这是因为数组已排序，后边元素更大，子集和一定超过 target
        if target - choices[i] < 0:
            break
        # 尝试：做出选择，更新 target, start
        state.append(choices[i])
        # 进行下一轮选择
        backtrack(state, target - choices[i], choices, i, res)
        # 回退：撤销选择，恢复到之前的状态
        state.pop()

def subset_sum_i(nums: list[int], target: int) -> list[list[int]]:
    """求解子集和 I"""
    state = []  # 状态（子集）
    nums.sort()  # 对 nums 进行排序
    start = 0  # 遍历起始点
    res = []  # 结果列表（子集列表）
    backtrack(state, target, nums, start, res)
    return res

subset_sum_i.go

[class]{}-[func]{backtrackI}

/* 求解子集和 I */
func subsetSumI(nums []int, target int) [][]int {
    s := subsetI{}
    state := make([]int, 0) // 状态（子集）
    sort.Ints(nums)         // 对 nums 进行排序
    start := 0              // 遍历起始点
    res := make([][]int, 0) // 结果列表（子集列表）
    s.backtrack(start, target, &state, &nums, &res)
    return res
}

subset_sum_i.js

[class]{}-[func]{backtrack}

[class]{}-[func]{subsetSumI}

subset_sum_i.ts

[class]{}-[func]{backtrack}

[class]{}-[func]{subsetSumI}

subset_sum_i.c

[class]{}-[func]{backtrack}

[class]{}-[func]{subsetSumI}

subset_sum_i.cs

/* 回溯算法：子集和 I */
void backtrack(List<int> state, int target, int[] choices, int start, List<List<int>> res) {
    // 子集和等于 target 时，记录解
    if (target == 0) {
        res.Add(new List<int>(state));
        return;
    }
    // 遍历所有选择
    // 剪枝二：从 start 开始遍历，避免生成重复子集
    for (int i = start; i < choices.Length; i++) {
        // 剪枝一：若子集和超过 target ，则直接结束循环
        // 这是因为数组已排序，后边元素更大，子集和一定超过 target
        if (target - choices[i] < 0) {
            break;
        }
        // 尝试：做出选择，更新 target, start
        state.Add(choices[i]);
        // 进行下一轮选择
        backtrack(state, target - choices[i], choices, i, res);
        // 回退：撤销选择，恢复到之前的状态
        state.RemoveAt(state.Count - 1);
    }
}

/* 求解子集和 I */
List<List<int>> subsetSumI(int[] nums, int target) {
    List<int> state = new List<int>(); // 状态（子集）
    Array.Sort(nums); // 对 nums 进行排序
    int start = 0; // 遍历起始点
    List<List<int>> res = new List<List<int>>(); // 结果列表（子集列表）
    backtrack(state, target, nums, start, res);
    return res;
}

subset_sum_i.swift

[class]{}-[func]{backtrack}

[class]{}-[func]{subsetSumI}

subset_sum_i.zig

[class]{}-[func]{backtrack}

[class]{}-[func]{subsetSumI}

subset_sum_i.dart

[class]{}-[func]{backtrack}

[class]{}-[func]{subsetSumI}

如下图所示，为将数组 \([3, 4, 5]\) 和目标元素 \(9\) 输入到以上代码后的整体回溯过程。

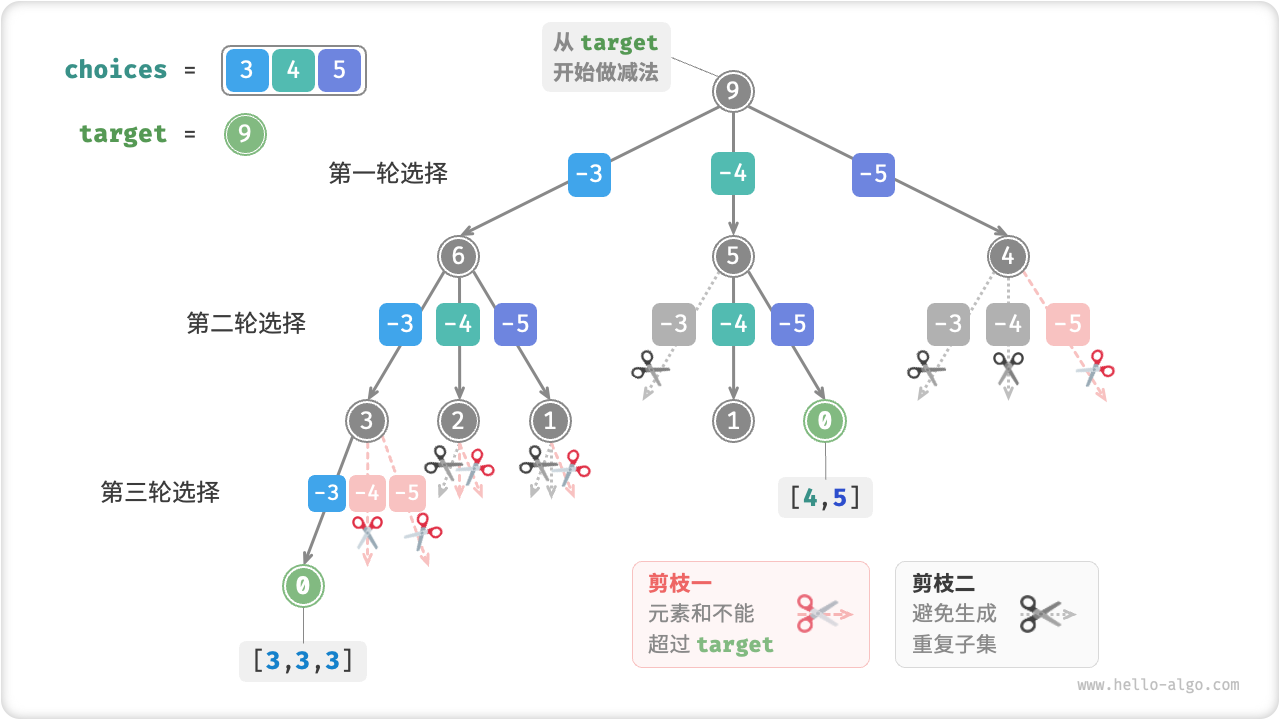
子集和 I 回溯过程

Fig. 子集和 I 回溯过程

12.3.3. 相等元素剪枝¶

Question

给定一个正整数数组 nums 和一个目标正整数 target ，请找出所有可能的组合，使得组合中的元素和等于 target 。给定数组可能包含重复元素，每个元素只可被选择一次。请以列表形式返回这些组合，列表中不应包含重复组合。

相比于上题，本题的输入数组可能包含重复元素，这引入了新的问题。例如，给定数组 \([4, \hat{4}, 5]\) 和目标元素 \(9\) ，则现有代码的输出结果为 \([4, 5], [\hat{4}, 5]\) ，也出现了重复子集。造成这种重复的原因是相等元素在某轮中被多次选择。如下图所示，第一轮共有三个选择，其中两个都为 \(4\) ，会产生两个重复的搜索分支，从而输出重复子集；同理，第二轮的两个 \(4\) 也会产生重复子集。

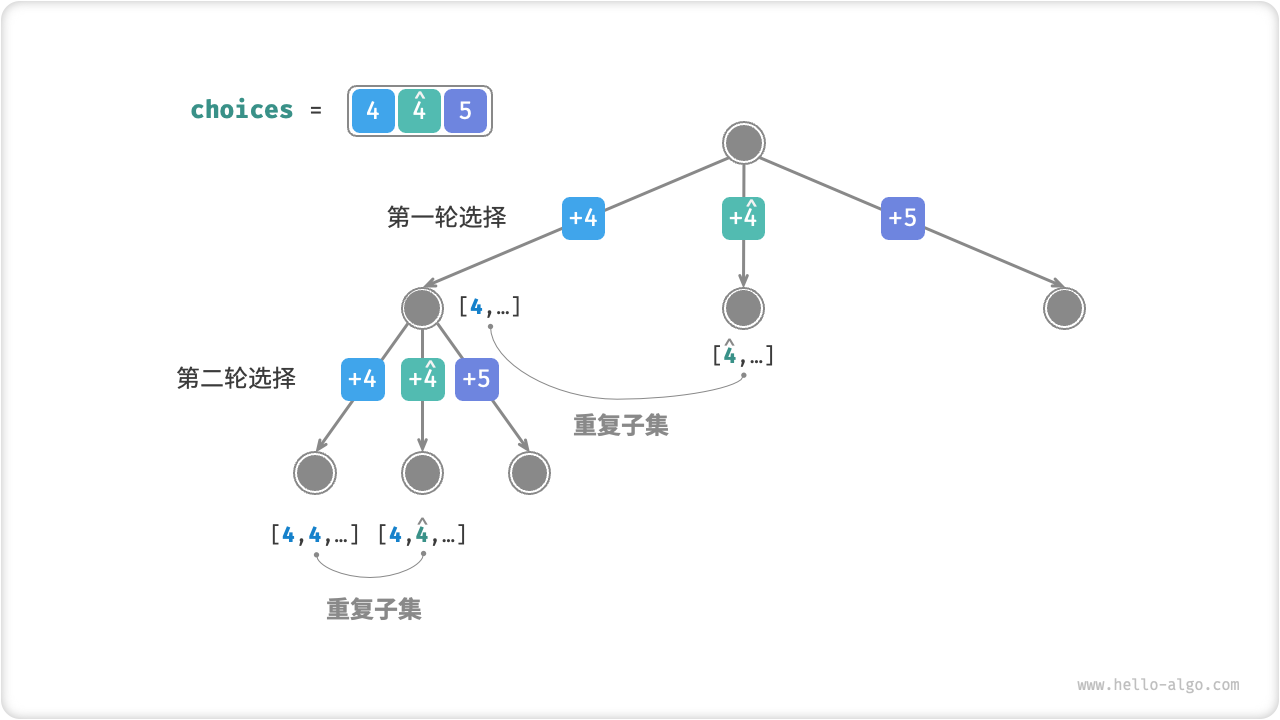
相等元素导致的重复子集

Fig. 相等元素导致的重复子集

为解决此问题，我们需要限制相等元素在每一轮中只被选择一次。实现方式比较巧妙：由于数组是已排序的，因此相等元素都是相邻的。利用该特性，在某轮选择中，若当前元素与其左边元素相等，则说明它已经被选择过，因此直接跳过当前元素。

与此同时，本题规定数组元素只能被选择一次。幸运的是，我们也可以利用变量 start 来满足该约束：当做出选择 \(x_{i}\) 后，设定下一轮从索引 \(i + 1\) 开始向后遍历。这样即能去除重复子集，也能避免重复选择相等元素。

JavaC++PythonGoJavaScriptTypeScriptCC#SwiftZigDart

subset_sum_ii.java

/* 回溯算法：子集和 II */
void backtrack(List<Integer> state, int target, int[] choices, int start, List<List<Integer>> res) {
    // 子集和等于 target 时，记录解
    if (target == 0) {
        res.add(new ArrayList<>(state));
        return;
    }
    // 遍历所有选择
    // 剪枝二：从 start 开始遍历，避免生成重复子集
    // 剪枝三：从 start 开始遍历，避免重复选择同一元素
    for (int i = start; i < choices.length; i++) {
        // 剪枝一：若子集和超过 target ，则直接结束循环
        // 这是因为数组已排序，后边元素更大，子集和一定超过 target
        if (target - choices[i] < 0) {
            break;
        }
        // 剪枝四：如果该元素与左边元素相等，说明该搜索分支重复，直接跳过
        if (i > start && choices[i] == choices[i - 1]) {
            continue;
        }
        // 尝试：做出选择，更新 target, start
        state.add(choices[i]);
        // 进行下一轮选择
        backtrack(state, target - choices[i], choices, i + 1, res);
        // 回退：撤销选择，恢复到之前的状态
        state.remove(state.size() - 1);
    }
}

/* 求解子集和 II */
List<List<Integer>> subsetSumII(int[] nums, int target) {
    List<Integer> state = new ArrayList<>(); // 状态（子集）
    Arrays.sort(nums); // 对 nums 进行排序
    int start = 0; // 遍历起始点
    List<List<Integer>> res = new ArrayList<>(); // 结果列表（子集列表）
    backtrack(state, target, nums, start, res);
    return res;
}

subset_sum_ii.cpp

/* 回溯算法：子集和 II */
void backtrack(vector<int> &state, int target, vector<int> &choices, int start, vector<vector<int>> &res) {
    // 子集和等于 target 时，记录解
    if (target == 0) {
        res.push_back(state);
        return;
    }
    // 遍历所有选择
    // 剪枝二：从 start 开始遍历，避免生成重复子集
    // 剪枝三：从 start 开始遍历，避免重复选择同一元素
    for (int i = start; i < choices.size(); i++) {
        // 剪枝一：若子集和超过 target ，则直接结束循环
        // 这是因为数组已排序，后边元素更大，子集和一定超过 target
        if (target - choices[i] < 0) {
            break;
        }
        // 剪枝四：如果该元素与左边元素相等，说明该搜索分支重复，直接跳过
        if (i > start && choices[i] == choices[i - 1]) {
            continue;
        }
        // 尝试：做出选择，更新 target, start
        state.push_back(choices[i]);
        // 进行下一轮选择
        backtrack(state, target - choices[i], choices, i + 1, res);
        // 回退：撤销选择，恢复到之前的状态
        state.pop_back();
    }
}

/* 求解子集和 II */
vector<vector<int>> subsetSumII(vector<int> &nums, int target) {
    vector<int> state;              // 状态（子集）
    sort(nums.begin(), nums.end()); // 对 nums 进行排序
    int start = 0;                  // 遍历起始点
    vector<vector<int>> res;        // 结果列表（子集列表）
    backtrack(state, target, nums, start, res);
    return res;
}

subset_sum_ii.py

def backtrack(
    state: list[int], target: int, choices: list[int], start: int, res: list[list[int]]
):
    """回溯算法：子集和 II"""
    # 子集和等于 target 时，记录解
    if target == 0:
        res.append(list(state))
        return
    # 遍历所有选择
    # 剪枝二：从 start 开始遍历，避免生成重复子集
    # 剪枝三：从 start 开始遍历，避免重复选择同一元素
    for i in range(start, len(choices)):
        # 剪枝一：若子集和超过 target ，则直接结束循环
        # 这是因为数组已排序，后边元素更大，子集和一定超过 target
        if target - choices[i] < 0:
            break
        # 剪枝四：如果该元素与左边元素相等，说明该搜索分支重复，直接跳过
        if i > start and choices[i] == choices[i - 1]:
            continue
        # 尝试：做出选择，更新 target, start
        state.append(choices[i])
        # 进行下一轮选择
        backtrack(state, target - choices[i], choices, i + 1, res)
        # 回退：撤销选择，恢复到之前的状态
        state.pop()

def subset_sum_ii(nums: list[int], target: int) -> list[list[int]]:
    """求解子集和 II"""
    state = []  # 状态（子集）
    nums.sort()  # 对 nums 进行排序
    start = 0  # 遍历起始点
    res = []  # 结果列表（子集列表）
    backtrack(state, target, nums, start, res)
    return res

subset_sum_ii.go

[class]{}-[func]{backtrackII}

/* 求解子集和 II */
func subsetSumII(nums []int, target int) [][]int {
    s := subsetII{}
    state := make([]int, 0) // 状态（子集）
    sort.Ints(nums)         // 对 nums 进行排序
    start := 0              // 遍历起始点
    res := make([][]int, 0) // 结果列表（子集列表）
    s.backtrack(start, target, &state, &nums, &res)
    return res
}

subset_sum_ii.js

[class]{}-[func]{backtrack}

[class]{}-[func]{subsetSumII}

subset_sum_ii.ts

[class]{}-[func]{backtrack}

[class]{}-[func]{subsetSumII}

subset_sum_ii.c

[class]{}-[func]{backtrack}

[class]{}-[func]{subsetSumII}

subset_sum_ii.cs

/* 回溯算法：子集和 II */
void backtrack(List<int> state, int target, int[] choices, int start, List<List<int>> res) {
    // 子集和等于 target 时，记录解
    if (target == 0) {
        res.Add(new List<int>(state));
        return;
    }
    // 遍历所有选择
    // 剪枝二：从 start 开始遍历，避免生成重复子集
    // 剪枝三：从 start 开始遍历，避免重复选择同一元素
    for (int i = start; i < choices.Length; i++) {
        // 剪枝一：若子集和超过 target ，则直接结束循环
        // 这是因为数组已排序，后边元素更大，子集和一定超过 target
        if (target - choices[i] < 0) {
            break;
        }
        // 剪枝四：如果该元素与左边元素相等，说明该搜索分支重复，直接跳过
        if (i > start && choices[i] == choices[i - 1]) {
            continue;
        }
        // 尝试：做出选择，更新 target, start
        state.Add(choices[i]);
        // 进行下一轮选择
        backtrack(state, target - choices[i], choices, i + 1, res);
        // 回退：撤销选择，恢复到之前的状态
        state.RemoveAt(state.Count - 1);
    }
}

/* 求解子集和 II */
List<List<int>> subsetSumII(int[] nums, int target) {
    List<int> state = new List<int>(); // 状态（子集）
    Array.Sort(nums); // 对 nums 进行排序
    int start = 0; // 遍历起始点
    List<List<int>> res = new List<List<int>>(); // 结果列表（子集列表）
    backtrack(state, target, nums, start, res);
    return res;
}

subset_sum_ii.swift

[class]{}-[func]{backtrack}

[class]{}-[func]{subsetSumII}

subset_sum_ii.zig

[class]{}-[func]{backtrack}

[class]{}-[func]{subsetSumII}

subset_sum_ii.dart

[class]{}-[func]{backtrack}

[class]{}-[func]{subsetSumII}

下图展示了数组 \([4, 4, 5]\) 和目标元素 \(9\) 的回溯过程，共包含四种剪枝操作。建议你将图示与代码注释相结合，理解整个搜索过程，以及每种剪枝操作是如何工作的。

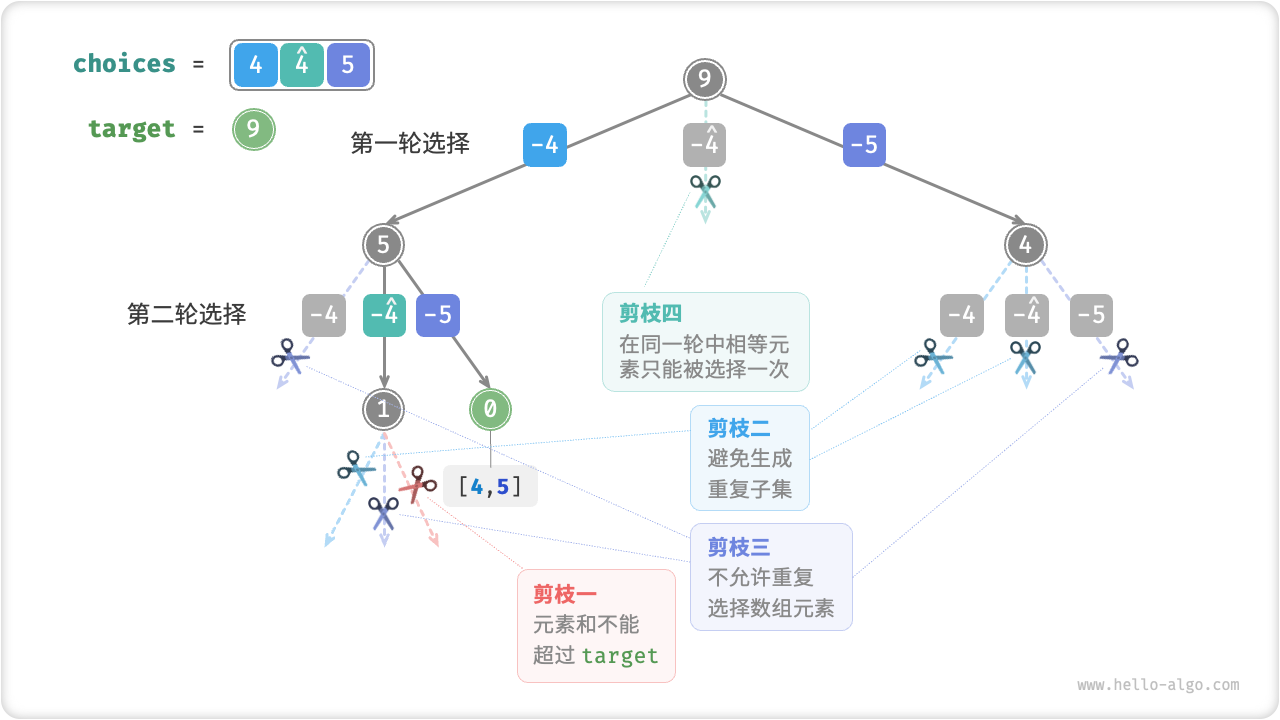
子集和 II 回溯过程

Fig. 子集和 II 回溯过程

12.3. 子集和问题¶

12.3.1. 从全排列引出解法¶

12.3.2. 重复子集剪枝¶

12.3.3. 相等元素剪枝¶

评论