7.2 Binary tree traversal¶
From the perspective of physical structure, a tree is a data structure based on linked lists, hence its traversal method involves accessing nodes one by one through pointers. However, a tree is a non-linear data structure, which makes traversing a tree more complex than traversing a linked list, requiring the assistance of search algorithms to achieve.
Common traversal methods for binary trees include level-order traversal, pre-order traversal, in-order traversal, and post-order traversal, among others.
7.2.1 Level-order traversal¶
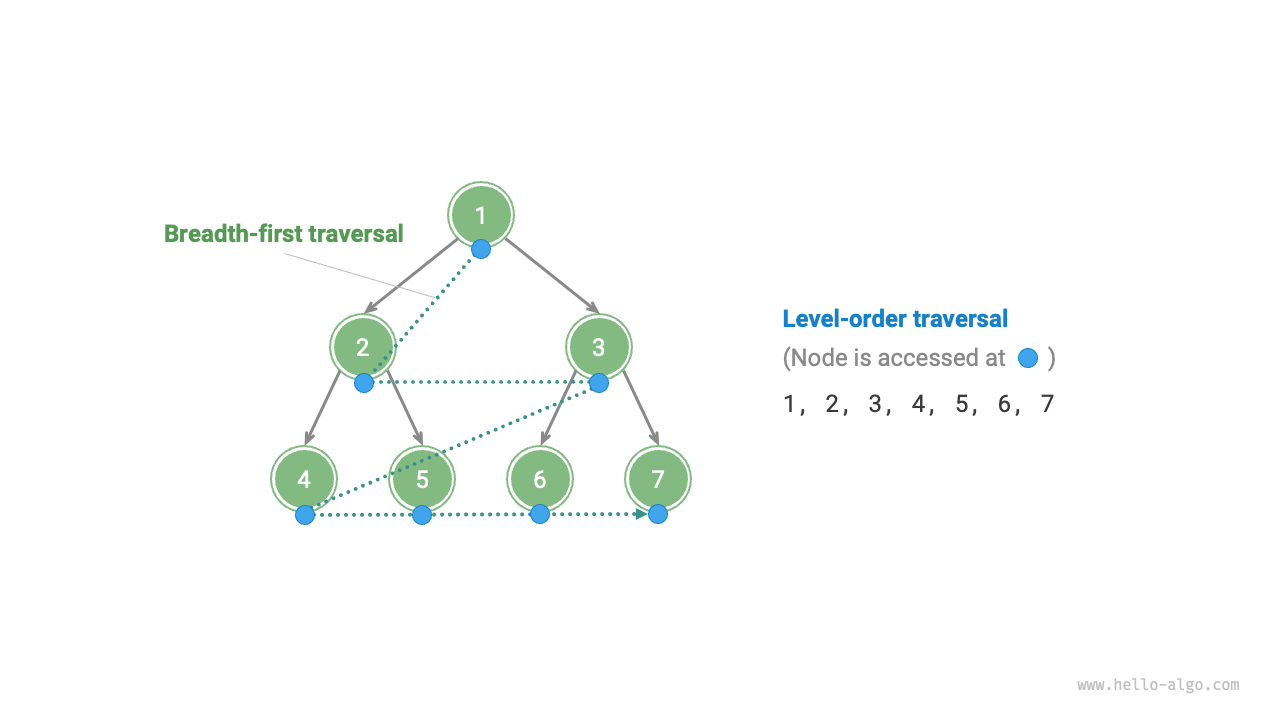
As shown in Figure 7-9, level-order traversal traverses the binary tree from top to bottom, layer by layer, and accesses nodes in each layer in a left-to-right order.
Level-order traversal essentially belongs to breadth-first traversal, also known as breadth-first search (BFS), which embodies a "circumferentially outward expanding" layer-by-layer traversal method.
Figure 7-9 Level-order traversal of a binary tree
1. Code implementation¶
Breadth-first traversal is usually implemented with the help of a "queue". The queue follows the "first in, first out" rule, while breadth-first traversal follows the "layer-by-layer progression" rule, the underlying ideas of the two are consistent. The implementation code is as follows:
def level_order(root: TreeNode | None) -> list[int]:
"""Level-order traversal"""
# Initialize queue, add root node
queue: deque[TreeNode] = deque()
queue.append(root)
# Initialize a list to store the traversal sequence
res = []
while queue:
node: TreeNode = queue.popleft() # Queue dequeues
res.append(node.val) # Save node value
if node.left is not None:
queue.append(node.left) # Left child node enqueues
if node.right is not None:
queue.append(node.right) # Right child node enqueues
return res
/* Level-order traversal */
vector<int> levelOrder(TreeNode *root) {
// Initialize queue, add root node
queue<TreeNode *> queue;
queue.push(root);
// Initialize a list to store the traversal sequence
vector<int> vec;
while (!queue.empty()) {
TreeNode *node = queue.front();
queue.pop(); // Queue dequeues
vec.push_back(node->val); // Save node value
if (node->left != nullptr)
queue.push(node->left); // Left child node enqueues
if (node->right != nullptr)
queue.push(node->right); // Right child node enqueues
}
return vec;
}
/* Level-order traversal */
List<Integer> levelOrder(TreeNode root) {
// Initialize queue, add root node
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
// Initialize a list to store the traversal sequence
List<Integer> list = new ArrayList<>();
while (!queue.isEmpty()) {
TreeNode node = queue.poll(); // Queue dequeues
list.add(node.val); // Save node value
if (node.left != null)
queue.offer(node.left); // Left child node enqueues
if (node.right != null)
queue.offer(node.right); // Right child node enqueues
}
return list;
}
2. Complexity analysis¶
- Time complexity is \(O(n)\): All nodes are visited once, using \(O(n)\) time, where \(n\) is the number of nodes.
- Space complexity is \(O(n)\): In the worst case, i.e., a full binary tree, before traversing to the lowest level, the queue can contain at most \((n + 1) / 2\) nodes at the same time, occupying \(O(n)\) space.
7.2.2 Preorder, in-order, and post-order traversal¶
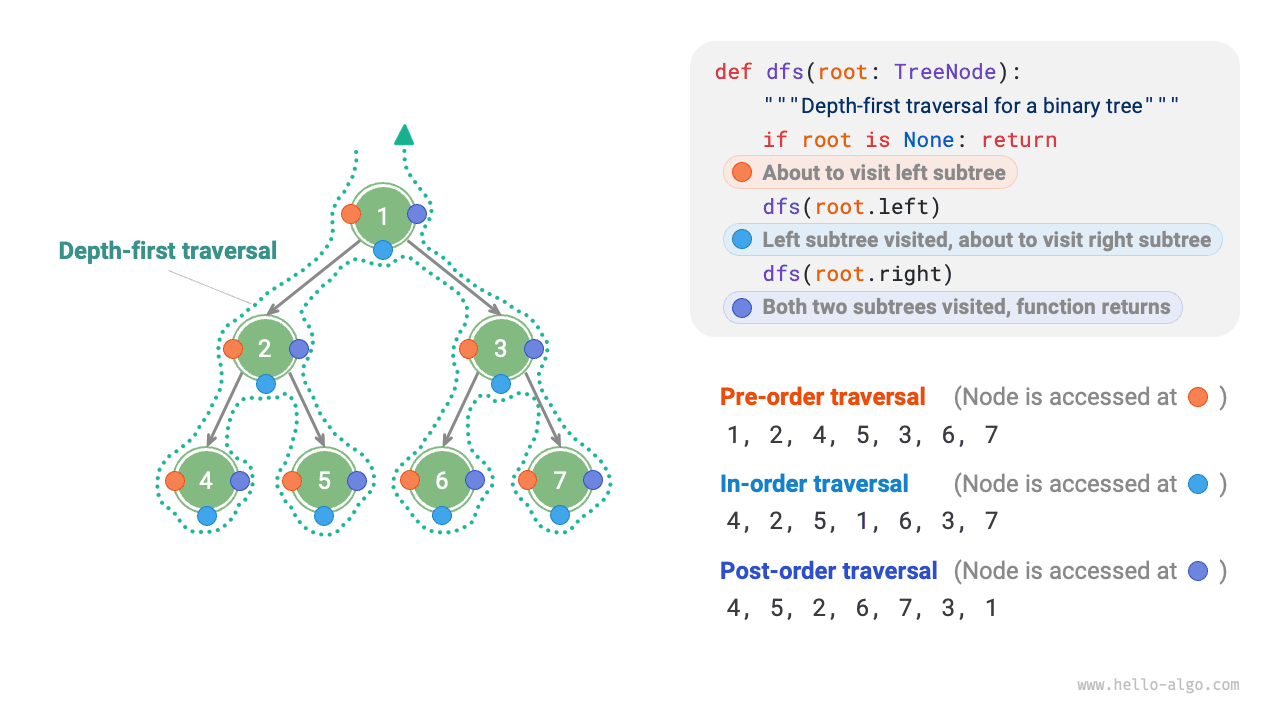
Correspondingly, pre-order, in-order, and post-order traversal all belong to depth-first traversal, also known as depth-first search (DFS), which embodies a "proceed to the end first, then backtrack and continue" traversal method.
Figure 7-10 shows the working principle of performing a depth-first traversal on a binary tree. Depth-first traversal is like walking around the perimeter of the entire binary tree, encountering three positions at each node, corresponding to pre-order traversal, in-order traversal, and post-order traversal.
Figure 7-10 Preorder, in-order, and post-order traversal of a binary search tree
1. Code implementation¶
Depth-first search is usually implemented based on recursion:
def pre_order(root: TreeNode | None):
"""Pre-order traversal"""
if root is None:
return
# Visit priority: root node -> left subtree -> right subtree
res.append(root.val)
pre_order(root=root.left)
pre_order(root=root.right)
def in_order(root: TreeNode | None):
"""In-order traversal"""
if root is None:
return
# Visit priority: left subtree -> root node -> right subtree
in_order(root=root.left)
res.append(root.val)
in_order(root=root.right)
def post_order(root: TreeNode | None):
"""Post-order traversal"""
if root is None:
return
# Visit priority: left subtree -> right subtree -> root node
post_order(root=root.left)
post_order(root=root.right)
res.append(root.val)
/* Pre-order traversal */
void preOrder(TreeNode *root) {
if (root == nullptr)
return;
// Visit priority: root node -> left subtree -> right subtree
vec.push_back(root->val);
preOrder(root->left);
preOrder(root->right);
}
/* In-order traversal */
void inOrder(TreeNode *root) {
if (root == nullptr)
return;
// Visit priority: left subtree -> root node -> right subtree
inOrder(root->left);
vec.push_back(root->val);
inOrder(root->right);
}
/* Post-order traversal */
void postOrder(TreeNode *root) {
if (root == nullptr)
return;
// Visit priority: left subtree -> right subtree -> root node
postOrder(root->left);
postOrder(root->right);
vec.push_back(root->val);
}
/* Pre-order traversal */
void preOrder(TreeNode root) {
if (root == null)
return;
// Visit priority: root node -> left subtree -> right subtree
list.add(root.val);
preOrder(root.left);
preOrder(root.right);
}
/* In-order traversal */
void inOrder(TreeNode root) {
if (root == null)
return;
// Visit priority: left subtree -> root node -> right subtree
inOrder(root.left);
list.add(root.val);
inOrder(root.right);
}
/* Post-order traversal */
void postOrder(TreeNode root) {
if (root == null)
return;
// Visit priority: left subtree -> right subtree -> root node
postOrder(root.left);
postOrder(root.right);
list.add(root.val);
}
Tip
Depth-first search can also be implemented based on iteration, interested readers can study this on their own.
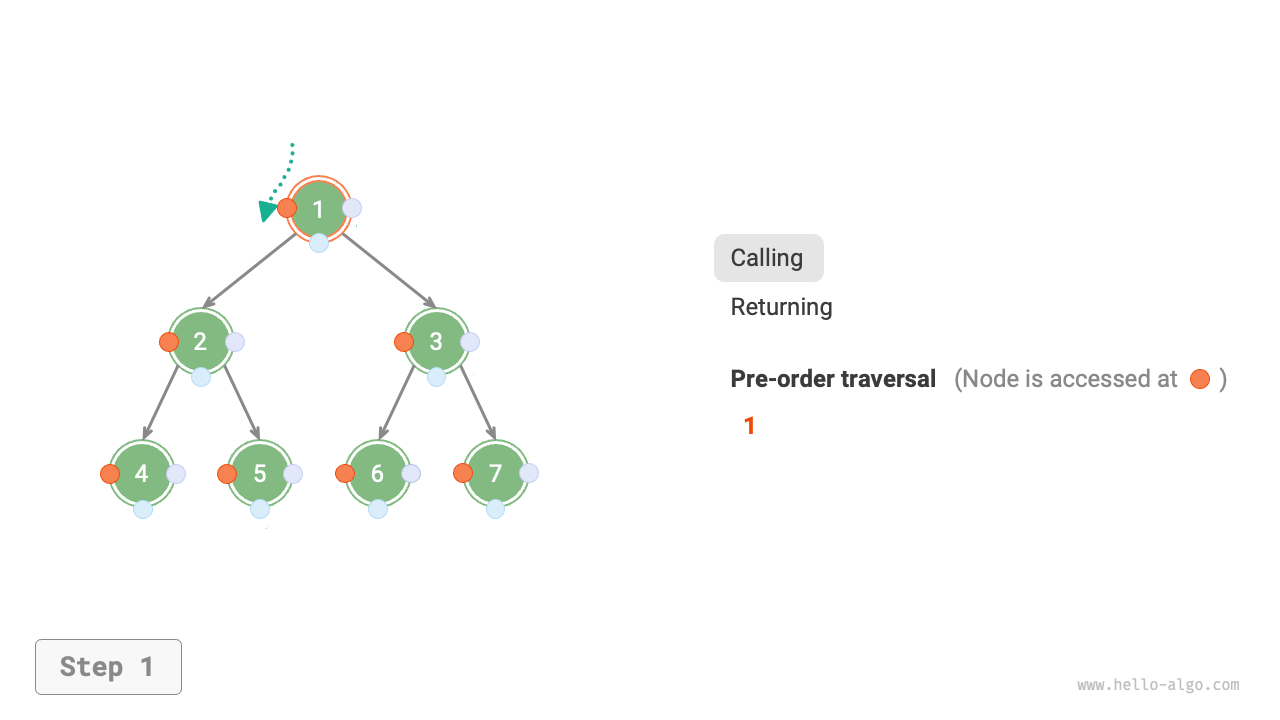
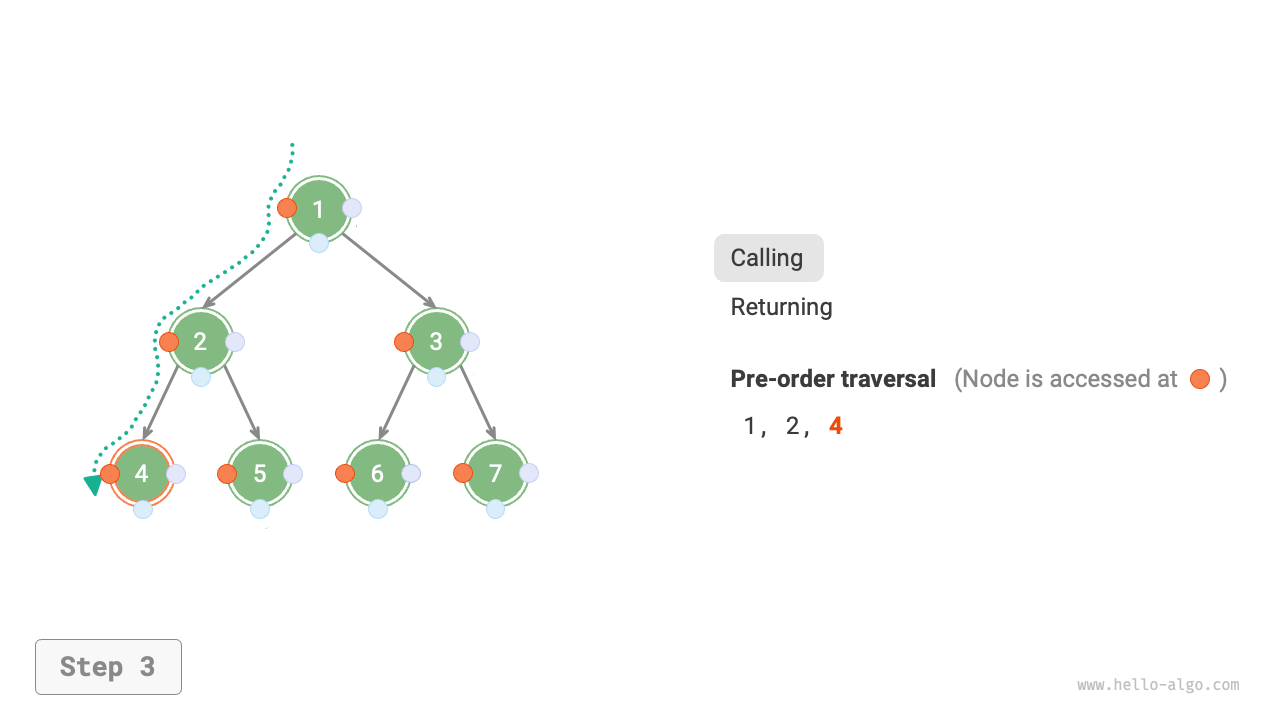
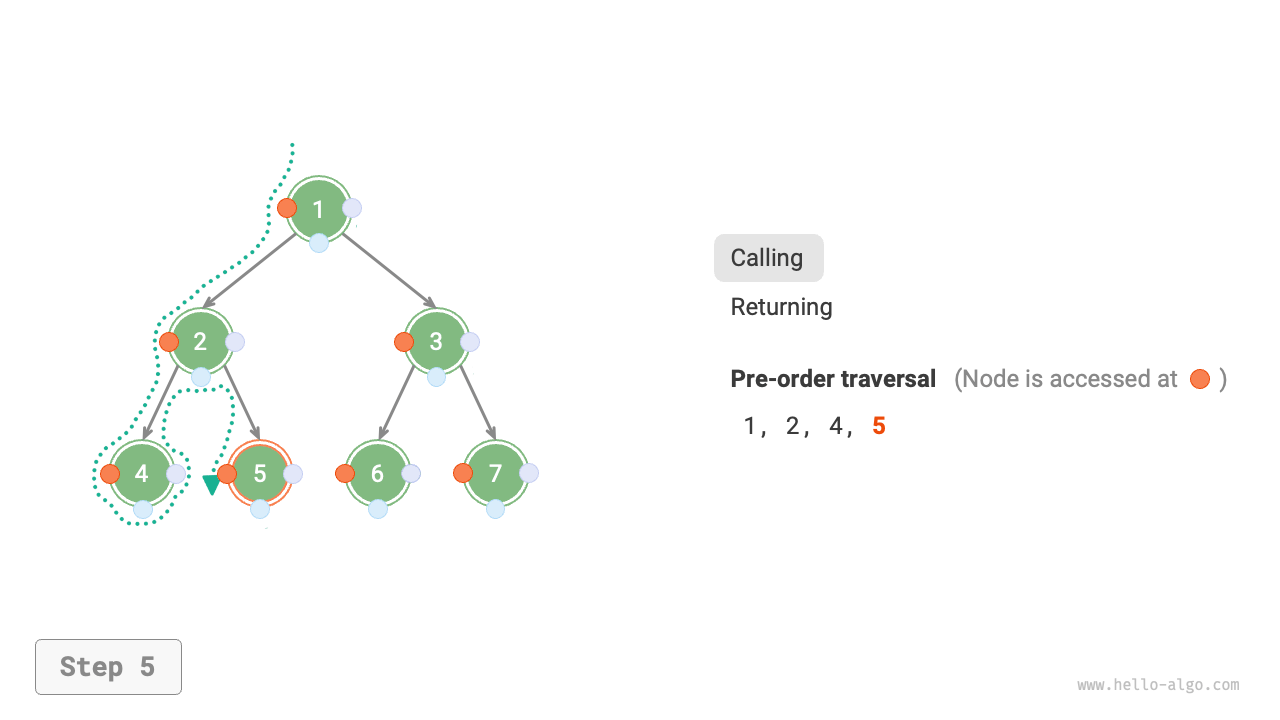
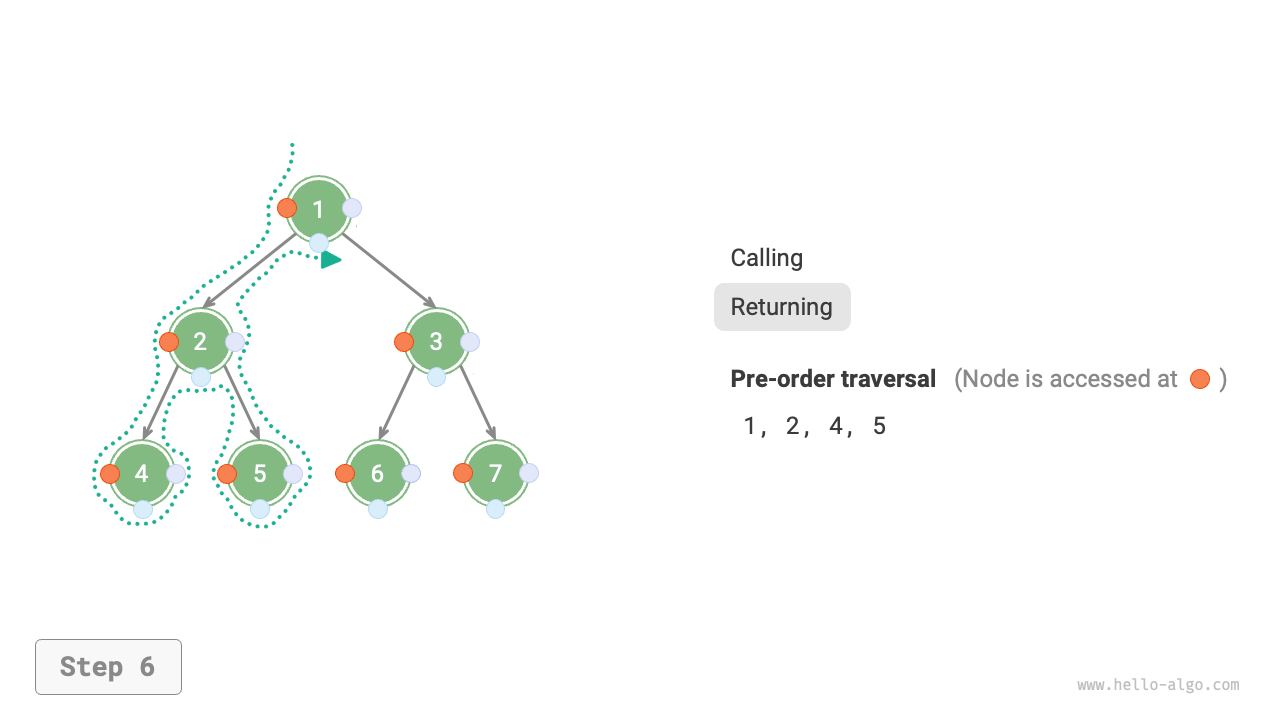
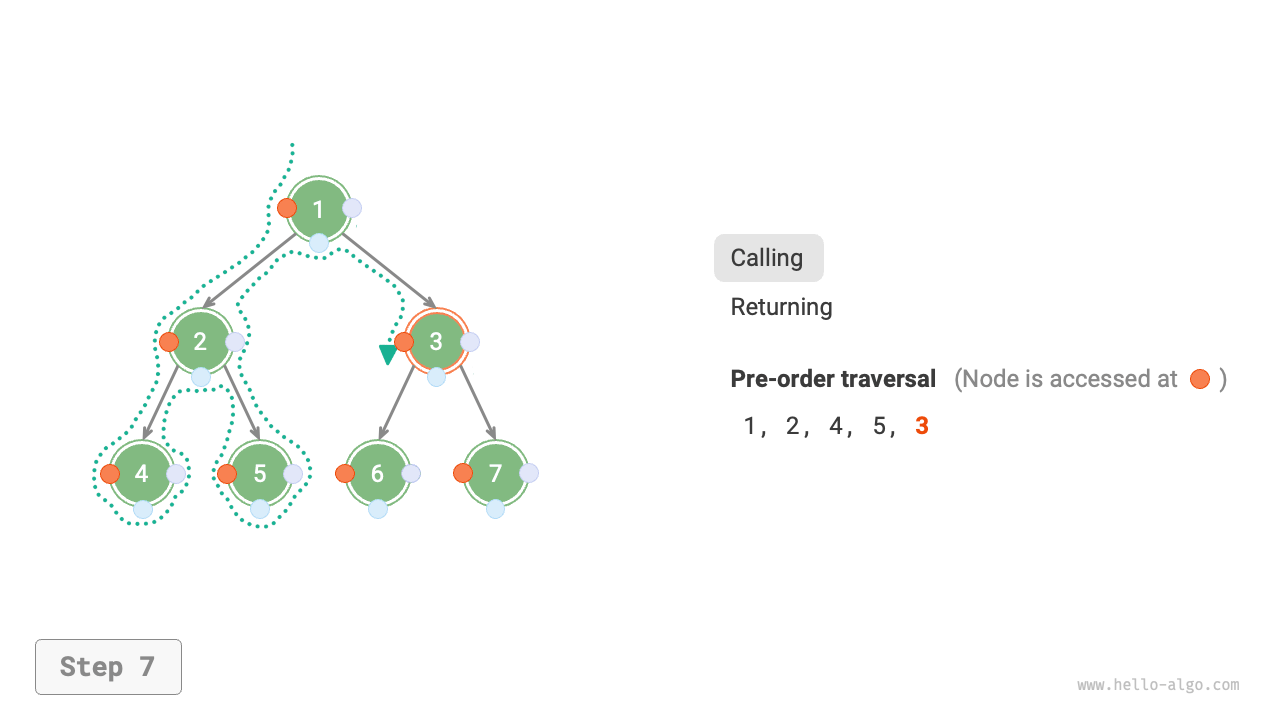
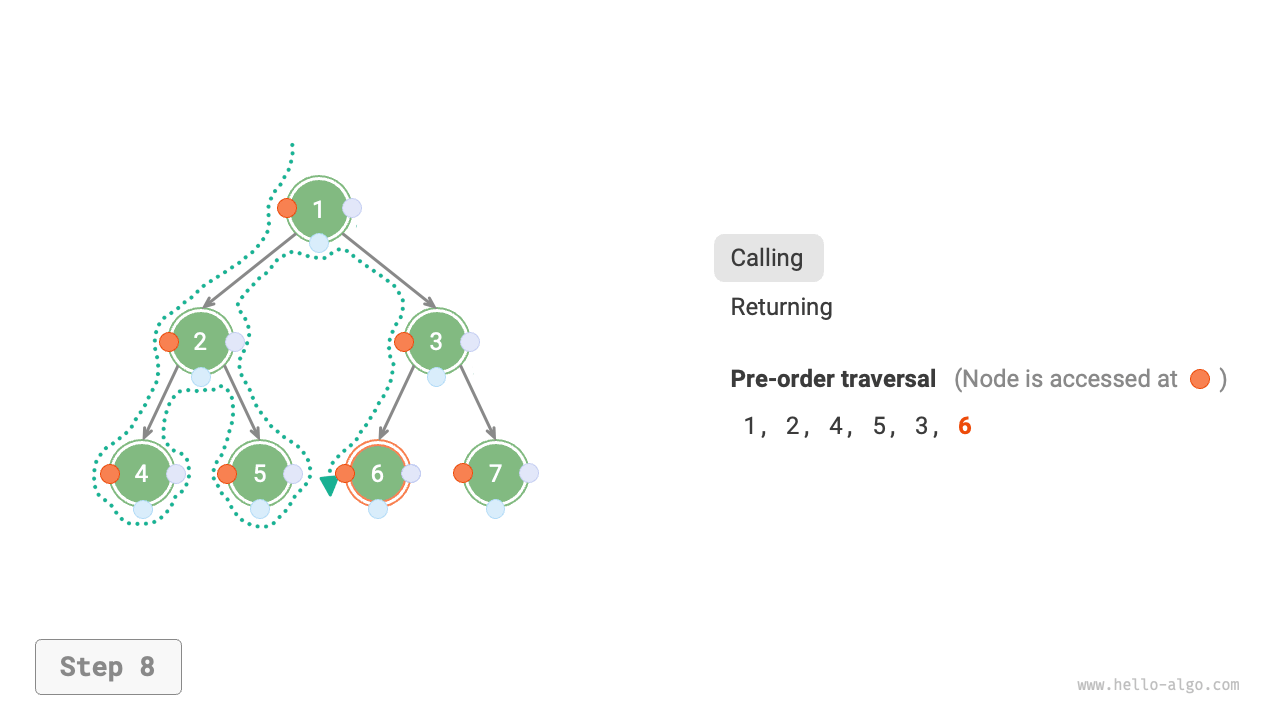
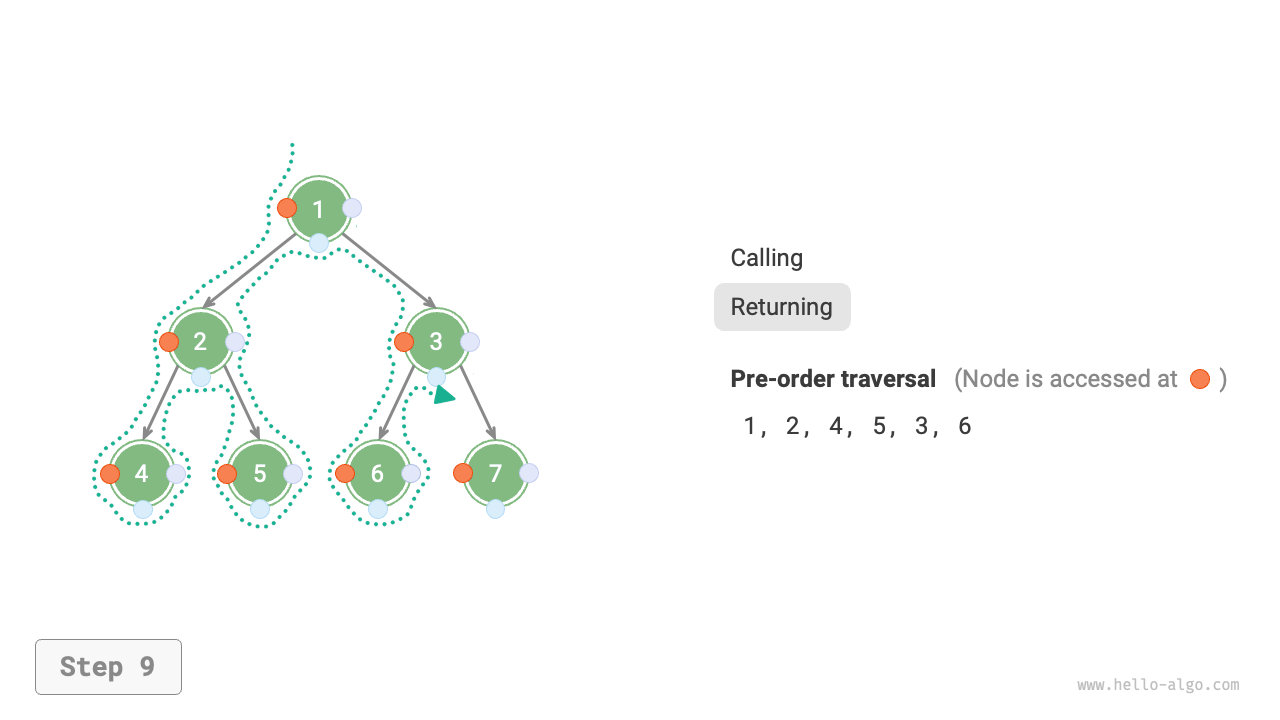
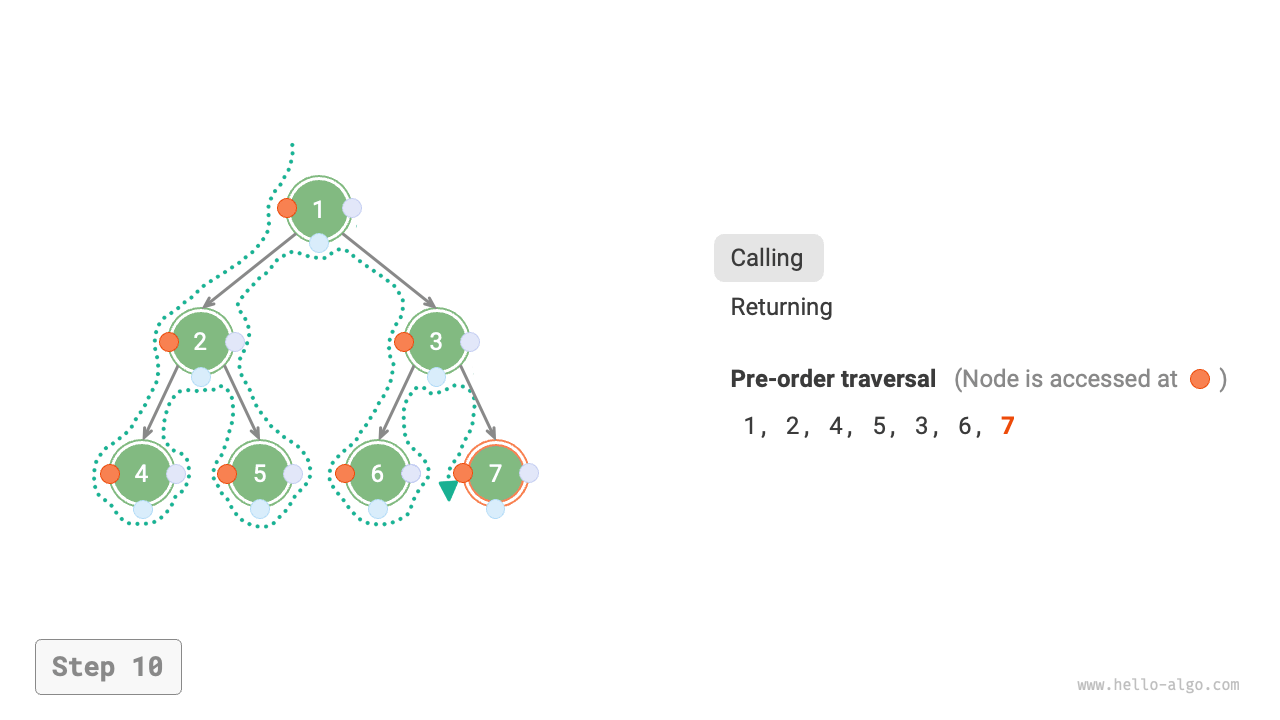
Figure 7-11 shows the recursive process of pre-order traversal of a binary tree, which can be divided into two opposite parts: "recursion" and "return".
- "Recursion" means starting a new method, the program accesses the next node in this process.
- "Return" means the function returns, indicating the current node has been fully accessed.
Figure 7-11 The recursive process of pre-order traversal
2. Complexity analysis¶
- Time complexity is \(O(n)\): All nodes are visited once, using \(O(n)\) time.
- Space complexity is \(O(n)\): In the worst case, i.e., the tree degrades into a linked list, the recursion depth reaches \(n\), the system occupies \(O(n)\) stack frame space.