7.4. AVL 树 *¶

在「二叉搜索树」章节中提到，在进行多次插入与删除操作后，二叉搜索树可能会退化为链表。此时所有操作的时间复杂度都会由 \(O(\log n)\) 劣化至 \(O(n)\) 。

如下图所示，执行两步删除结点后，该二叉搜索树就会退化为链表。

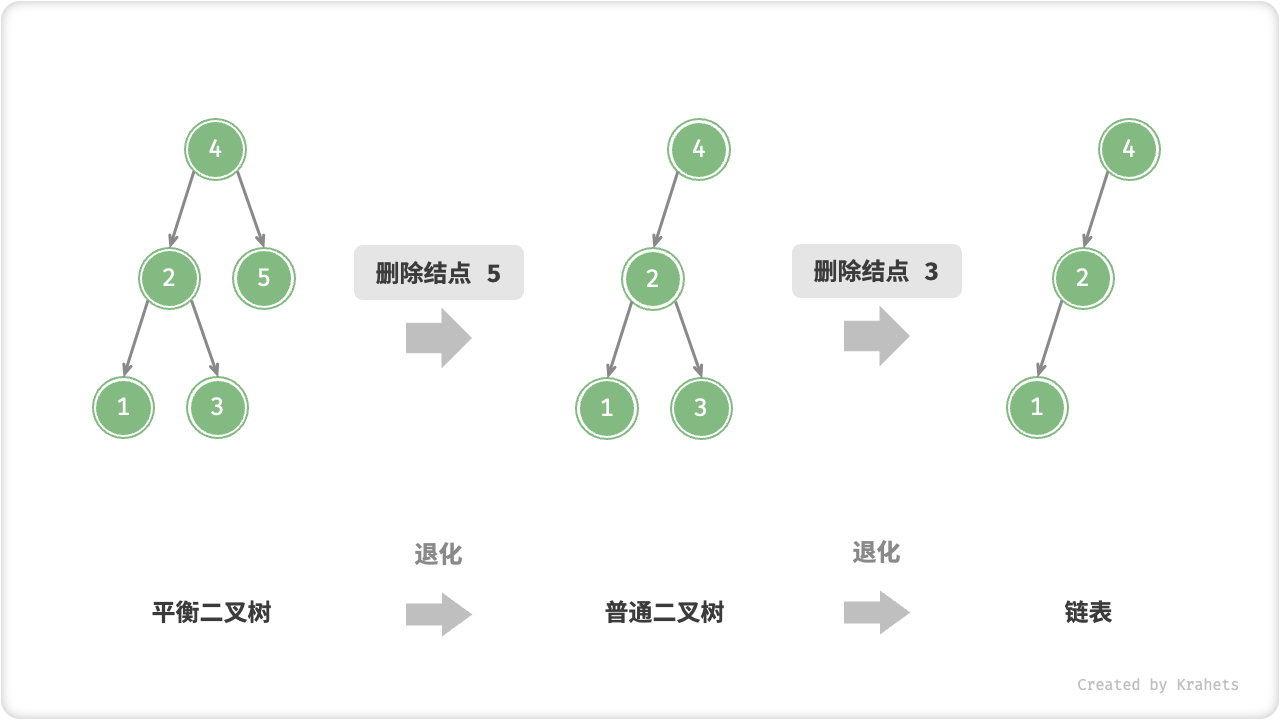
AVL 树在删除结点后发生退化

Fig. AVL 树在删除结点后发生退化

再比如，在以下完美二叉树中插入两个结点后，树严重向左偏斜，查找操作的时间复杂度也随之发生劣化。

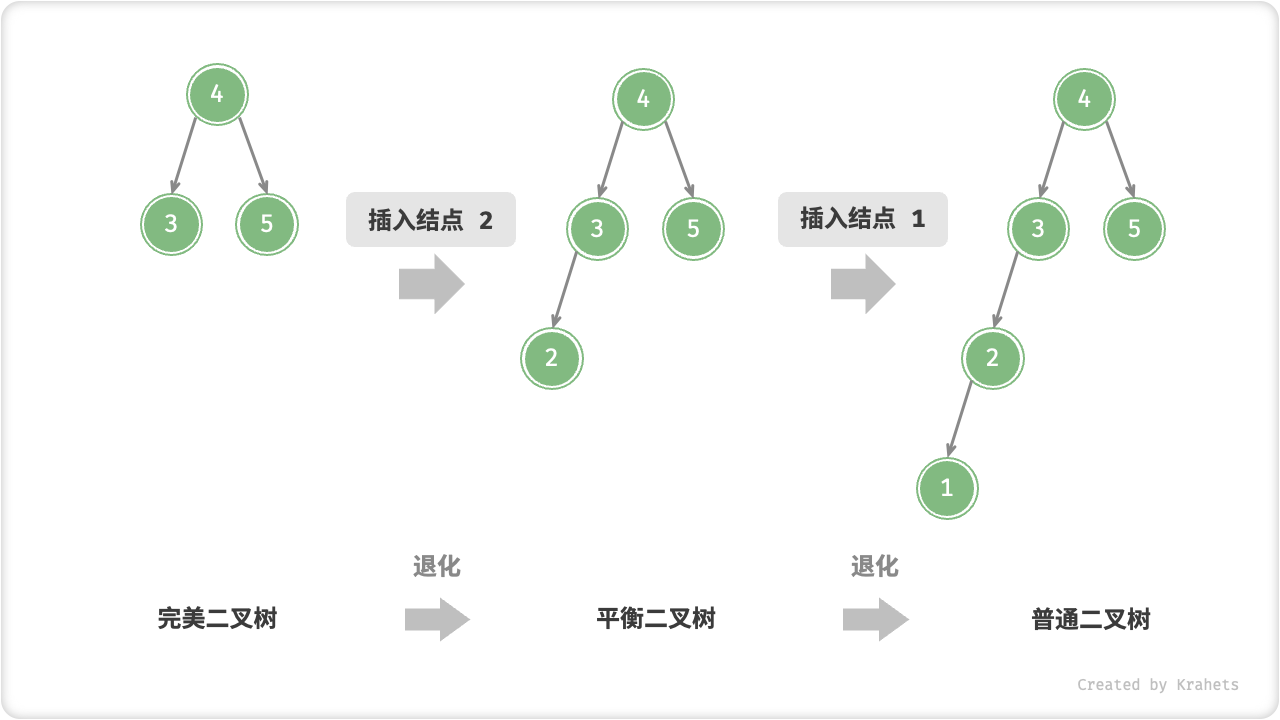
AVL 树在插入结点后发生退化

Fig. AVL 树在插入结点后发生退化

G. M. Adelson-Velsky 和 E. M. Landis 在其 1962 年发表的论文 "An algorithm for the organization of information" 中提出了「AVL 树」。论文中描述了一系列操作，使得在不断添加与删除结点后，AVL 树仍然不会发生退化，进而使得各种操作的时间复杂度均能保持在 \(O(\log n)\) 级别。

换言之，在频繁增删查改的使用场景中，AVL 树可始终保持很高的数据增删查改效率，具有很好的应用价值。

7.4.1. AVL 树常见术语¶

「AVL 树」既是「二叉搜索树」又是「平衡二叉树」，同时满足这两种二叉树的所有性质，因此又被称为「平衡二叉搜索树」。

结点高度¶

在 AVL 树的操作中，需要获取结点「高度 Height」，所以给 AVL 树的结点类添加 height 变量。

JavaC++PythonGoJavaScriptTypeScriptCC#SwiftZig

/* AVL 树结点类 */
class TreeNode {
    public int val;        // 结点值
    public int height;     // 结点高度
    public TreeNode left;  // 左子结点
    public TreeNode right; // 右子结点
    public TreeNode(int x) { val = x; }
}

/* AVL 树结点类 */
struct TreeNode {
    int val{};          // 结点值
    int height = 0;     // 结点高度
    TreeNode *left{};   // 左子结点
    TreeNode *right{};  // 右子结点
    TreeNode() = default;
    explicit TreeNode(int x) : val(x){}
};

""" AVL 树结点类 """
class TreeNode:
    def __init__(self, val: int):
        self.val: int = val                    # 结点值
        self.height: int = 0                   # 结点高度
        self.left: Optional[TreeNode] = None   # 左子结点引用
        self.right: Optional[TreeNode] = None  # 右子结点引用

/* AVL 树结点类 */
type TreeNode struct {
    Val    int       // 结点值
    Height int       // 结点高度
    Left   *TreeNode // 左子结点引用
    Right  *TreeNode // 右子结点引用
}

class TreeNode {
    val; // 结点值
    height; //结点高度
    left; // 左子结点指针
    right; // 右子结点指针
    constructor(val, left, right, height) {
        this.val = val === undefined ? 0 : val;
        this.height = height === undefined ? 0 : height;
        this.left = left === undefined ? null : left;
        this.right = right === undefined ? null : right;
    }
}

class TreeNode {
    val: number;            // 结点值
    height: number;         // 结点高度
    left: TreeNode | null;  // 左子结点指针
    right: TreeNode | null; // 右子结点指针
    constructor(val?: number, height?: number, left?: TreeNode | null, right?: TreeNode | null) {
        this.val = val === undefined ? 0 : val;
        this.height = height === undefined ? 0 : height; 
        this.left = left === undefined ? null : left; 
        this.right = right === undefined ? null : right; 
    }
}

/* AVL 树结点类 */
class TreeNode {
    public int val;          // 结点值
    public int height;       // 结点高度
    public TreeNode? left;   // 左子结点
    public TreeNode? right;  // 右子结点
    public TreeNode(int x) { val = x; }
}

/* AVL 树结点类 */
class TreeNode {
    var val: Int // 结点值
    var height: Int // 结点高度
    var left: TreeNode? // 左子结点
    var right: TreeNode? // 右子结点

    init(x: Int) {
        val = x
        height = 0
    }
}

「结点高度」是最远叶结点到该结点的距离，即走过的「边」的数量。需要特别注意，叶结点的高度为 0 ，空结点的高度为 -1。我们封装两个工具函数，分别用于获取与更新结点的高度。

JavaC++PythonGoJavaScriptTypeScriptCC#SwiftZig

avl_tree.java

/* 获取结点高度 */
int height(TreeNode node) {
    // 空结点高度为 -1 ，叶结点高度为 0
    return node == null ? -1 : node.height;
}

/* 更新结点高度 */
void updateHeight(TreeNode node) {
    // 结点高度等于最高子树高度 + 1
    node.height = Math.max(height(node.left), height(node.right)) + 1;
}

avl_tree.cpp

/* 获取结点高度 */
int height(TreeNode* node) {
    // 空结点高度为 -1 ，叶结点高度为 0
    return node == nullptr ? -1 : node->height;
}

/* 更新结点高度 */
void updateHeight(TreeNode* node) {
    // 结点高度等于最高子树高度 + 1
    node->height = max(height(node->left), height(node->right)) + 1;
}

avl_tree.py

def height(self, node: TreeNode | None) -> int:
    """ 获取结点高度 """
    # 空结点高度为 -1 ，叶结点高度为 0
    if node is not None:
        return node.height
    return -1

def __update_height(self, node: TreeNode | None):
    """ 更新结点高度 """
    # 结点高度等于最高子树高度 + 1
    node.height = max([self.height(node.left), self.height(node.right)]) + 1

avl_tree.go

/* 获取结点高度 */
func (t *aVLTree) height(node *TreeNode) int {
    // 空结点高度为 -1 ，叶结点高度为 0
    if node != nil {
        return node.Height
    }
    return -1
}

/* 更新结点高度 */
func (t *aVLTree) updateHeight(node *TreeNode) {
    lh := t.height(node.Left)
    rh := t.height(node.Right)
    // 结点高度等于最高子树高度 + 1
    if lh > rh {
        node.Height = lh + 1
    } else {
        node.Height = rh + 1
    }
}

avl_tree.js

/* 获取结点高度 */
height(node) {
    // 空结点高度为 -1 ，叶结点高度为 0
    return node === null ? -1 : node.height;
}

/* 更新结点高度 */
#updateHeight(node) {
    // 结点高度等于最高子树高度 + 1
    node.height = Math.max(this.height(node.left), this.height(node.right)) + 1;
}

avl_tree.ts

/* 获取结点高度 */
height(node: TreeNode): number {
    // 空结点高度为 -1 ，叶结点高度为 0
    return node === null ? -1 : node.height;
}

/* 更新结点高度 */
updateHeight(node: TreeNode): void {
    // 结点高度等于最高子树高度 + 1
    node.height = Math.max(this.height(node.left), this.height(node.right)) + 1;
}

avl_tree.c

[class]{aVLTree}-[func]{height}

[class]{aVLTree}-[func]{updateHeight}

avl_tree.cs

/* 获取结点高度 */
int height(TreeNode? node)
{
    // 空结点高度为 -1 ，叶结点高度为 0
    return node == null ? -1 : node.height;
}

/* 更新结点高度 */
void updateHeight(TreeNode node)
{
    // 结点高度等于最高子树高度 + 1
    node.height = Math.Max(height(node.left), height(node.right)) + 1;
}

avl_tree.swift

/* 获取结点高度 */
func height(node: TreeNode?) -> Int {
    // 空结点高度为 -1 ，叶结点高度为 0
    node == nil ? -1 : node!.height
}

/* 更新结点高度 */
func updateHeight(node: TreeNode?) {
    // 结点高度等于最高子树高度 + 1
    node?.height = max(height(node: node?.left), height(node: node?.right)) + 1
}

avl_tree.zig

// 获取结点高度
fn height(self: *Self, node: ?*inc.TreeNode(T)) i32 {
    _ = self;
    // 空结点高度为 -1 ，叶结点高度为 0
    return if (node == null) -1 else node.?.height;
}

// 更新结点高度
fn updateHeight(self: *Self, node: ?*inc.TreeNode(T)) void {
    // 结点高度等于最高子树高度 + 1
    node.?.height = std.math.max(self.height(node.?.left), self.height(node.?.right)) + 1;
}

结点平衡因子¶

结点的「平衡因子 Balance Factor」是 结点的左子树高度减去右子树高度，并定义空结点的平衡因子为 0 。同样地，我们将获取结点平衡因子封装成函数，以便后续使用。

JavaC++PythonGoJavaScriptTypeScriptCC#SwiftZig

avl_tree.java

/* 获取平衡因子 */
int balanceFactor(TreeNode node) {
    // 空结点平衡因子为 0
    if (node == null) return 0;
    // 结点平衡因子 = 左子树高度 - 右子树高度
    return height(node.left) - height(node.right);
}

avl_tree.cpp

/* 获取平衡因子 */
int balanceFactor(TreeNode* node) {
    // 空结点平衡因子为 0
    if (node == nullptr) return 0;
    // 结点平衡因子 = 左子树高度 - 右子树高度
    return height(node->left) - height(node->right);
}

avl_tree.py

def balance_factor(self, node: TreeNode | None) -> int:
    """ 获取平衡因子 """
    # 空结点平衡因子为 0
    if node is None:
        return 0
    # 结点平衡因子 = 左子树高度 - 右子树高度
    return self.height(node.left) - self.height(node.right)

avl_tree.go

/* 获取平衡因子 */
func (t *aVLTree) balanceFactor(node *TreeNode) int {
    // 空结点平衡因子为 0
    if node == nil {
        return 0
    }
    // 结点平衡因子 = 左子树高度 - 右子树高度
    return t.height(node.Left) - t.height(node.Right)
}

avl_tree.js

/* 获取平衡因子 */
balanceFactor(node) {
    // 空结点平衡因子为 0
    if (node === null) return 0;
    // 结点平衡因子 = 左子树高度 - 右子树高度
    return this.height(node.left) - this.height(node.right);
}

avl_tree.ts

/* 获取平衡因子 */
balanceFactor(node: TreeNode): number {
    // 空结点平衡因子为 0
    if (node === null) return 0;
    // 结点平衡因子 = 左子树高度 - 右子树高度
    return this.height(node.left) - this.height(node.right);
}

avl_tree.c

[class]{aVLTree}-[func]{balanceFactor}

avl_tree.cs

/* 获取平衡因子 */
int balanceFactor(TreeNode? node)
{
    // 空结点平衡因子为 0
    if (node == null) return 0;
    // 结点平衡因子 = 左子树高度 - 右子树高度
    return height(node.left) - height(node.right);
}

avl_tree.swift

/* 获取平衡因子 */
func balanceFactor(node: TreeNode?) -> Int {
    // 空结点平衡因子为 0
    guard let node = node else { return 0 }
    // 结点平衡因子 = 左子树高度 - 右子树高度
    return height(node: node.left) - height(node: node.right)
}

avl_tree.zig

// 获取平衡因子
fn balanceFactor(self: *Self, node: ?*inc.TreeNode(T)) i32 {
    // 空结点平衡因子为 0
    if (node == null) return 0;
    // 结点平衡因子 = 左子树高度 - 右子树高度
    return self.height(node.?.left) - self.height(node.?.right);
}

Note

设平衡因子为 \(f\) ，则一棵 AVL 树的任意结点的平衡因子皆满足 \(-1 \le f \le 1\) 。

7.4.2. AVL 树旋转¶

AVL 树的独特之处在于「旋转 Rotation」的操作，其可 在不影响二叉树中序遍历序列的前提下，使失衡结点重新恢复平衡。换言之，旋转操作既可以使树保持为「二叉搜索树」，也可以使树重新恢复为「平衡二叉树」。

我们将平衡因子的绝对值 \(> 1\) 的结点称为「失衡结点」。根据结点的失衡情况，旋转操作分为 右旋、左旋、先右旋后左旋、先左旋后右旋，接下来我们来一起来看看它们是如何操作的。

Case 1 - 右旋¶

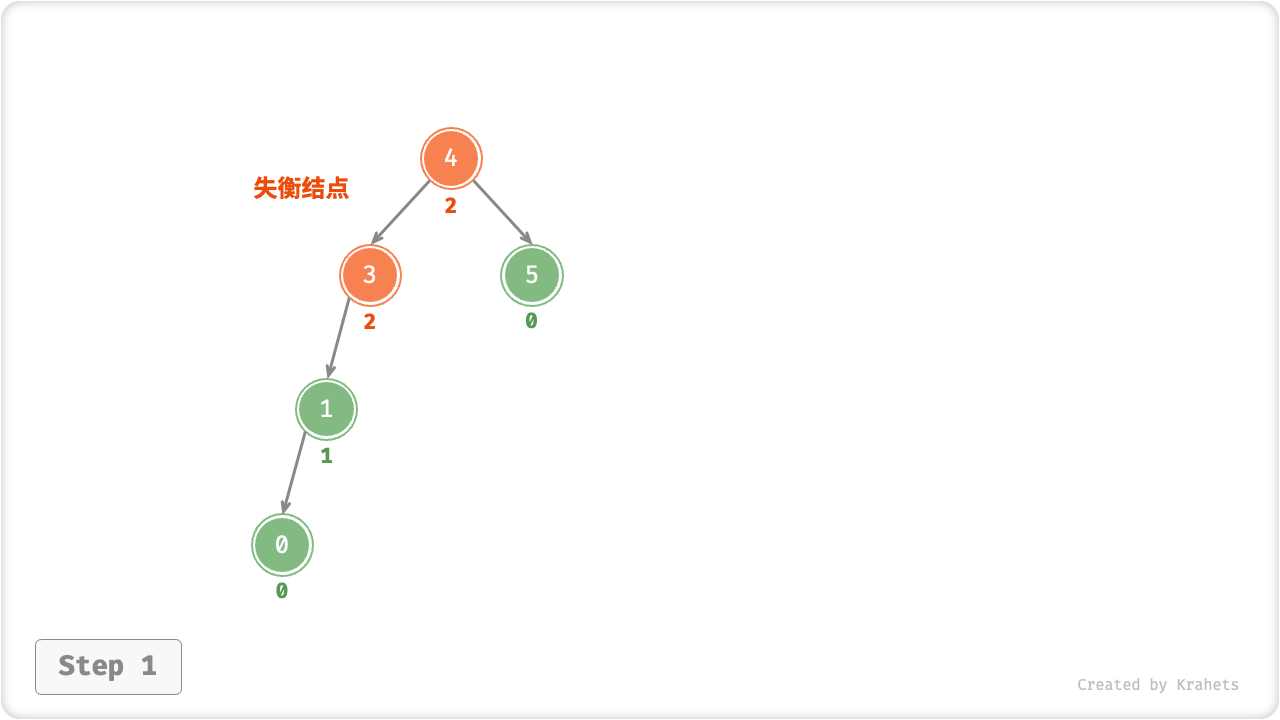
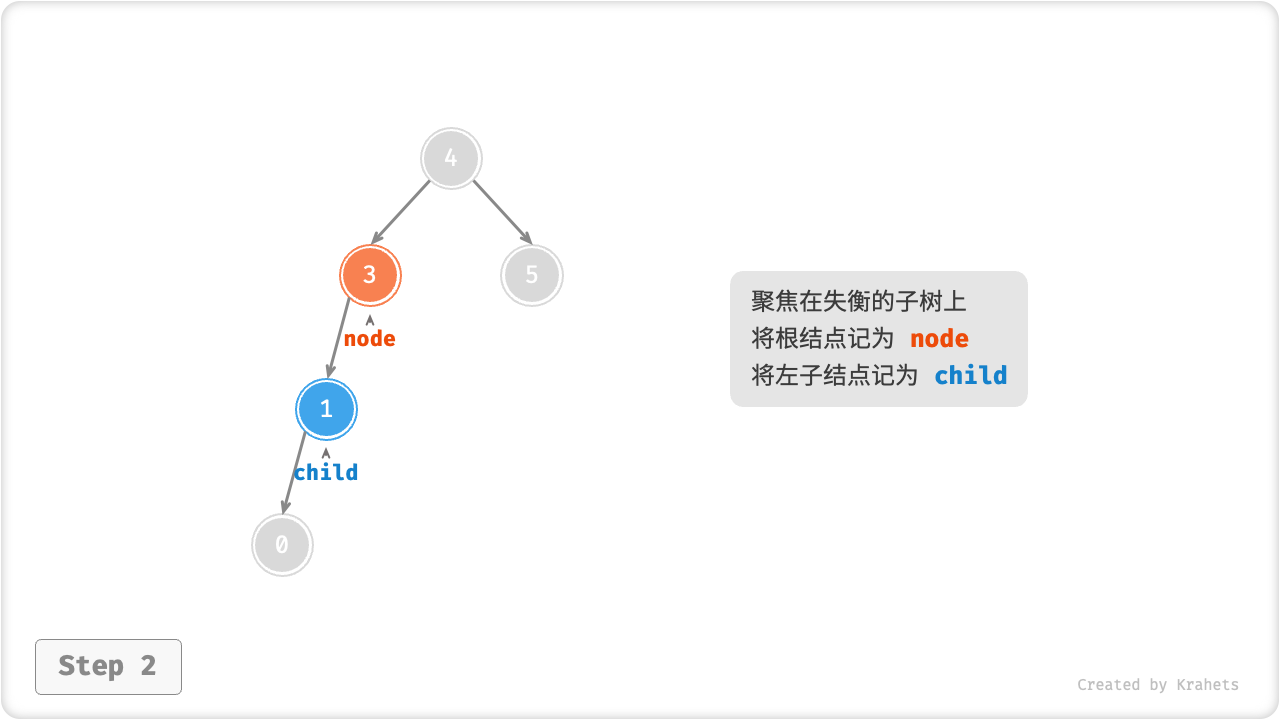
如下图所示（结点下方为「平衡因子」），从底至顶看，二叉树中首个失衡结点是 结点 3。我们聚焦在以该失衡结点为根结点的子树上，将该结点记为 node ，将其左子结点记为 child ，执行「右旋」操作。完成右旋后，该子树已经恢复平衡，并且仍然为二叉搜索树。

<1><2><3><4>

右旋操作步骤

avltree_right_rotate_step2

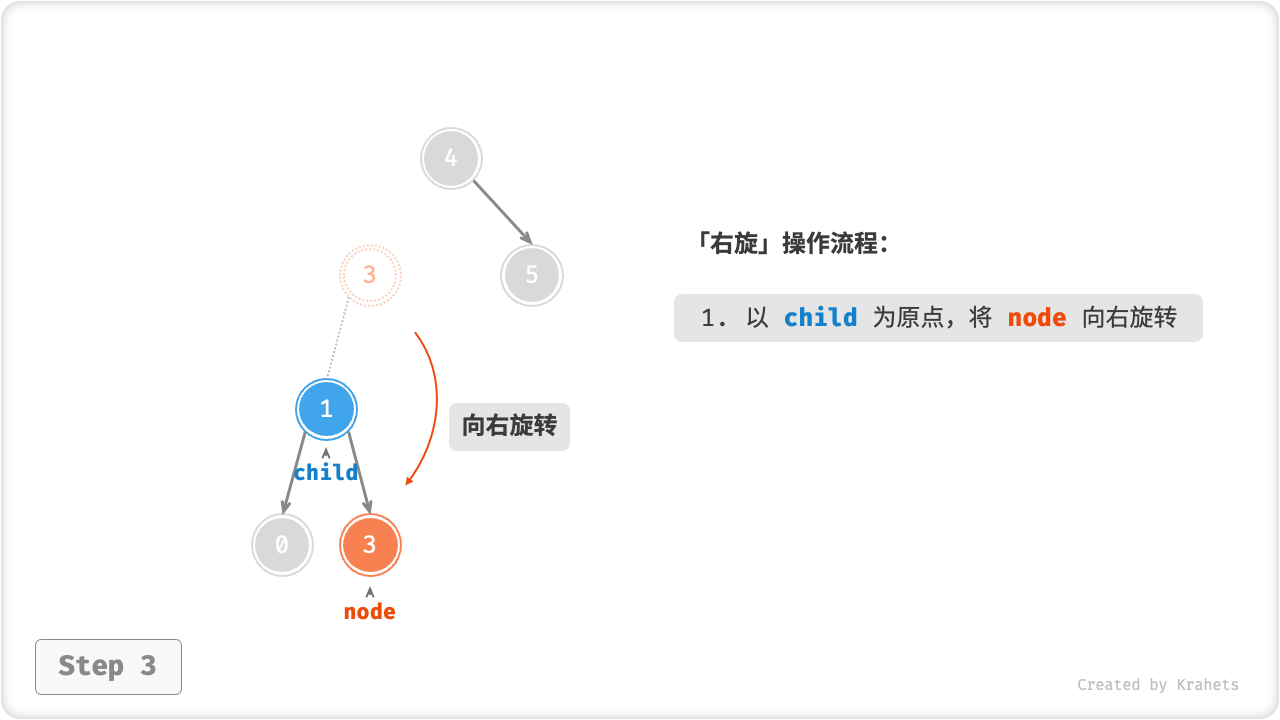
avltree_right_rotate_step3

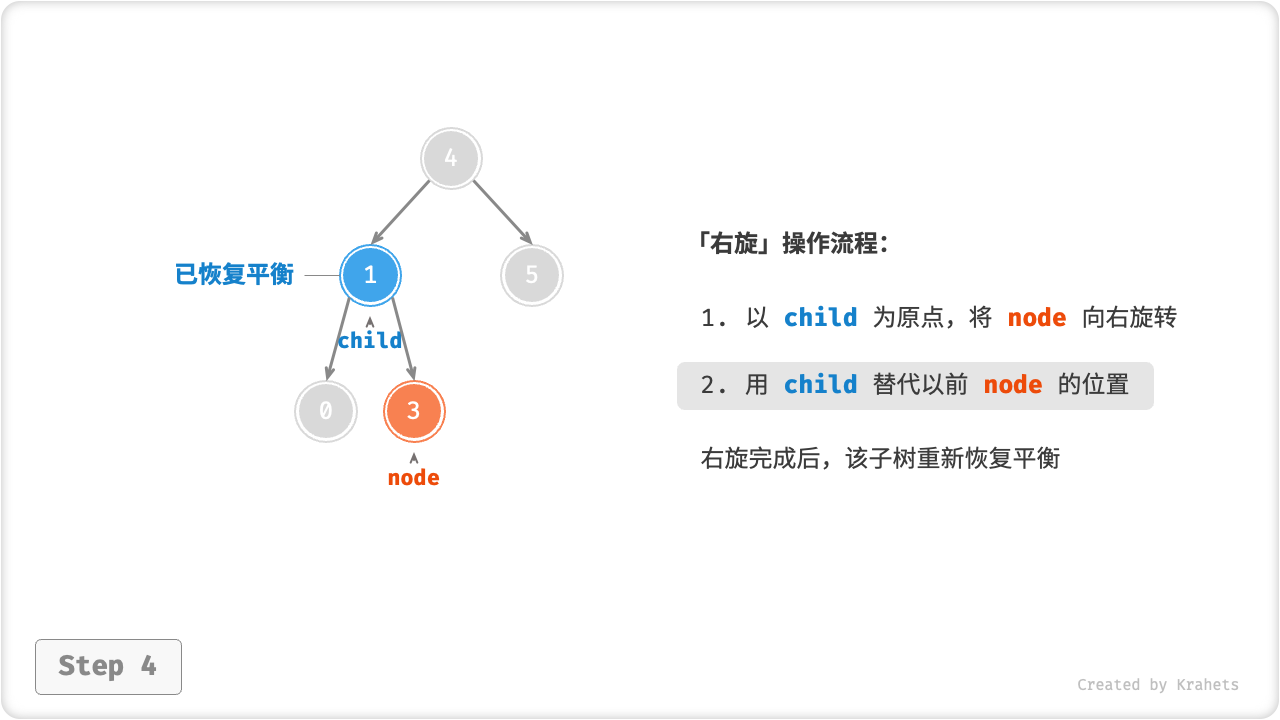
avltree_right_rotate_step4

进而，如果结点 child 本身有右子结点（记为 grandChild ），则需要在「右旋」中添加一步：将 grandChild 作为 node 的左子结点。

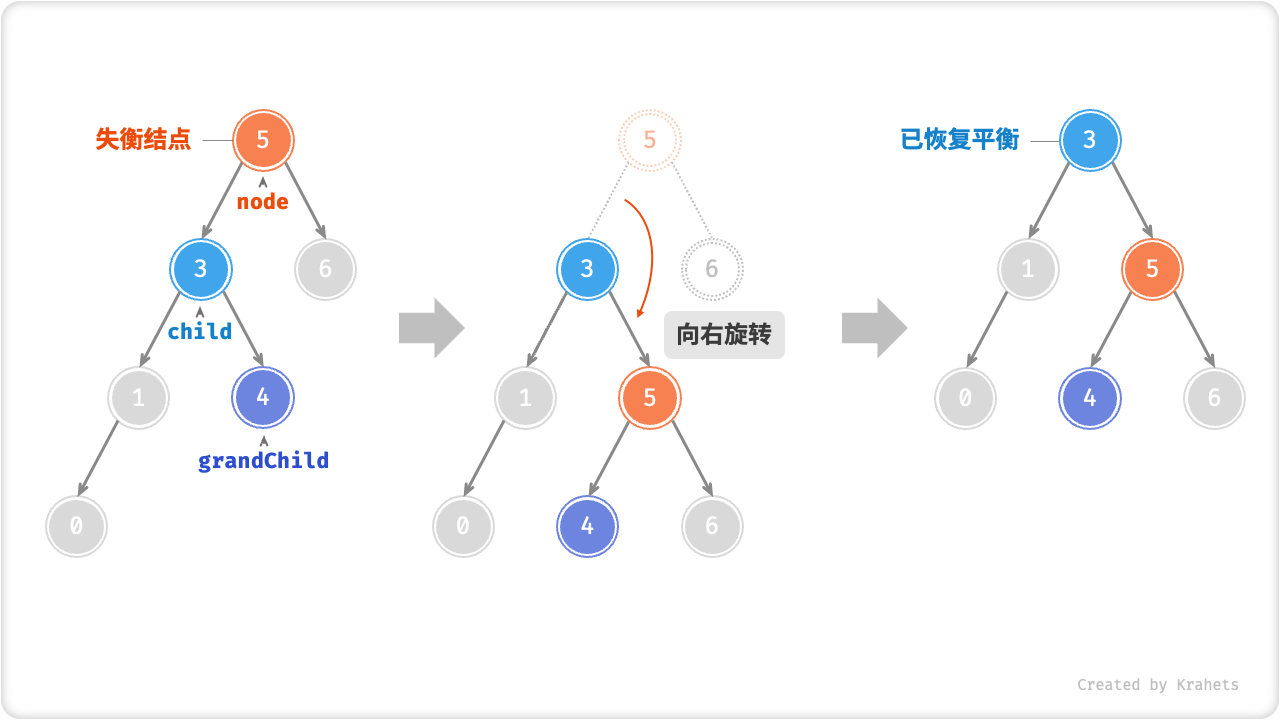
有 grandChild 的右旋操作

Fig. 有 grandChild 的右旋操作

“向右旋转”是一种形象化的说法，实际需要通过修改结点指针实现，代码如下所示。

JavaC++PythonGoJavaScriptTypeScriptCC#SwiftZig

avl_tree.java

/* 右旋操作 */
TreeNode rightRotate(TreeNode node) {
    TreeNode child = node.left;
    TreeNode grandChild = child.right;
    // 以 child 为原点，将 node 向右旋转
    child.right = node;
    node.left = grandChild;
    // 更新结点高度
    updateHeight(node);
    updateHeight(child);
    // 返回旋转后子树的根结点
    return child;
}

avl_tree.cpp

/* 右旋操作 */
TreeNode* rightRotate(TreeNode* node) {
    TreeNode* child = node->left;
    TreeNode* grandChild = child->right;
    // 以 child 为原点，将 node 向右旋转
    child->right = node;
    node->left = grandChild;
    // 更新结点高度
    updateHeight(node);
    updateHeight(child);
    // 返回旋转后子树的根结点
    return child;
}

avl_tree.py

def __right_rotate(self, node: TreeNode | None) -> TreeNode | None:
    """ 右旋操作 """
    child = node.left
    grand_child = child.right
    # 以 child 为原点，将 node 向右旋转
    child.right = node
    node.left = grand_child
    # 更新结点高度
    self.__update_height(node)
    self.__update_height(child)
    # 返回旋转后子树的根结点
    return child

avl_tree.go

/* 右旋操作 */
func (t *aVLTree) rightRotate(node *TreeNode) *TreeNode {
    child := node.Left
    grandChild := child.Right
    // 以 child 为原点，将 node 向右旋转
    child.Right = node
    node.Left = grandChild
    // 更新结点高度
    t.updateHeight(node)
    t.updateHeight(child)
    // 返回旋转后子树的根结点
    return child
}

avl_tree.js

/* 右旋操作 */
#rightRotate(node) {
    const child = node.left;
    const grandChild = child.right;
    // 以 child 为原点，将 node 向右旋转
    child.right = node;
    node.left = grandChild;
    // 更新结点高度
    this.#updateHeight(node);
    this.#updateHeight(child);
    // 返回旋转后子树的根结点
    return child;
}

avl_tree.ts

/* 右旋操作 */
rightRotate(node: TreeNode): TreeNode {
    const child = node.left;
    const grandChild = child.right;
    // 以 child 为原点，将 node 向右旋转
    child.right = node;
    node.left = grandChild;
    // 更新结点高度
    this.updateHeight(node);
    this.updateHeight(child);
    // 返回旋转后子树的根结点
    return child;
}

avl_tree.c

[class]{aVLTree}-[func]{rightRotate}

avl_tree.cs

/* 右旋操作 */
TreeNode? rightRotate(TreeNode? node)
{
    TreeNode? child = node.left;
    TreeNode? grandChild = child?.right;
    // 以 child 为原点，将 node 向右旋转
    child.right = node;
    node.left = grandChild;
    // 更新结点高度
    updateHeight(node);
    updateHeight(child);
    // 返回旋转后子树的根结点
    return child;
}

avl_tree.swift

/* 右旋操作 */
func rightRotate(node: TreeNode?) -> TreeNode? {
    let child = node?.left
    let grandChild = child?.right
    // 以 child 为原点，将 node 向右旋转
    child?.right = node
    node?.left = grandChild
    // 更新结点高度
    updateHeight(node: node)
    updateHeight(node: child)
    // 返回旋转后子树的根结点
    return child
}

avl_tree.zig

// 右旋操作
fn rightRotate(self: *Self, node: ?*inc.TreeNode(T)) ?*inc.TreeNode(T) {
    var child = node.?.left;
    var grandChild = child.?.right;
    // 以 child 为原点，将 node 向右旋转
    child.?.right = node;
    node.?.left = grandChild;
    // 更新结点高度
    self.updateHeight(node);
    self.updateHeight(child);
    // 返回旋转后子树的根结点
    return child;
}

Case 2 - 左旋¶

类似地，如果将取上述失衡二叉树的“镜像”，那么则需要「左旋」操作。

左旋操作

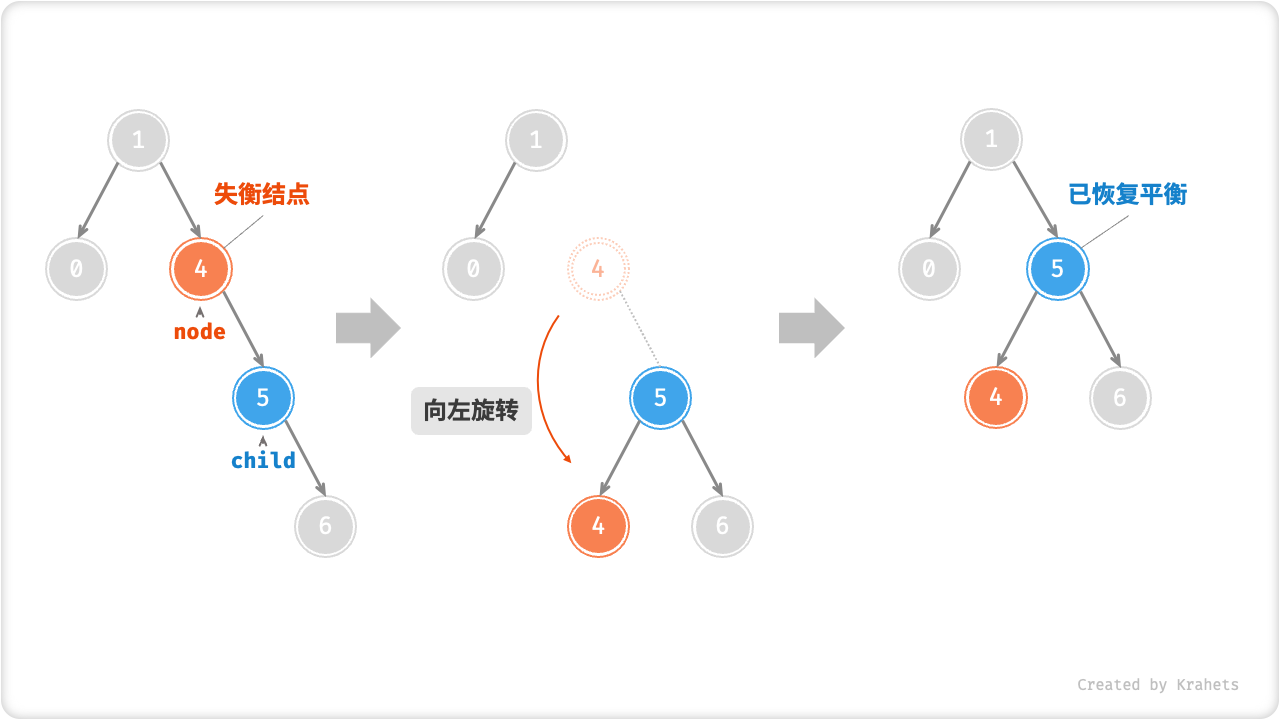
Fig. 左旋操作

同理，若结点 child 本身有左子结点（记为 grandChild ），则需要在「左旋」中添加一步：将 grandChild 作为 node 的右子结点。

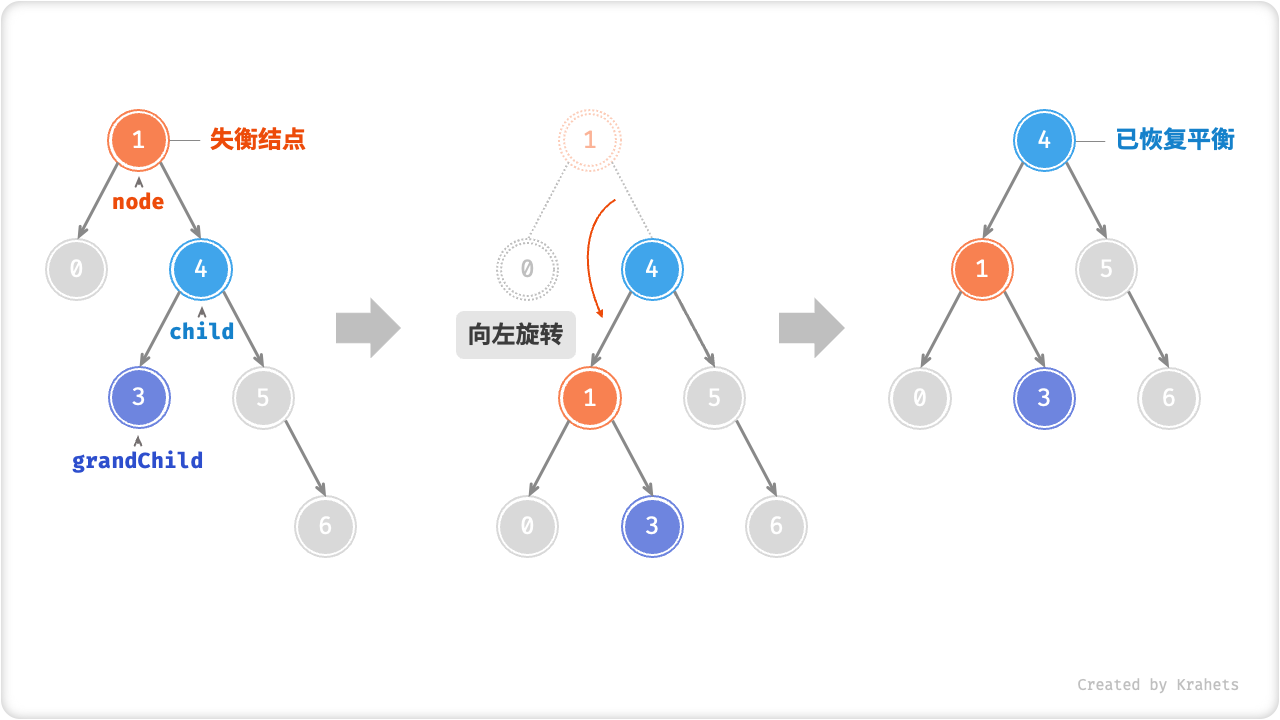
有 grandChild 的左旋操作

Fig. 有 grandChild 的左旋操作

观察发现，「左旋」和「右旋」操作是镜像对称的，两者对应解决的两种失衡情况也是对称的。根据对称性，我们可以很方便地从「右旋」推导出「左旋」。具体地，只需将「右旋」代码中的把所有的 left 替换为 right 、所有的 right 替换为 left ，即可得到「左旋」代码。

JavaC++PythonGoJavaScriptTypeScriptCC#SwiftZig

avl_tree.java

/* 左旋操作 */
TreeNode leftRotate(TreeNode node) {
    TreeNode child = node.right;
    TreeNode grandChild = child.left;
    // 以 child 为原点，将 node 向左旋转
    child.left = node;
    node.right = grandChild;
    // 更新结点高度
    updateHeight(node);
    updateHeight(child);
    // 返回旋转后子树的根结点
    return child;
}

avl_tree.cpp

/* 左旋操作 */
TreeNode* leftRotate(TreeNode* node) {
    TreeNode* child = node->right;
    TreeNode* grandChild = child->left;
    // 以 child 为原点，将 node 向左旋转
    child->left = node;
    node->right = grandChild;
    // 更新结点高度
    updateHeight(node);
    updateHeight(child);
    // 返回旋转后子树的根结点
    return child;
}

avl_tree.py

def __left_rotate(self, node: TreeNode | None) -> TreeNode | None:
    """ 左旋操作 """
    child = node.right
    grand_child = child.left
    # 以 child 为原点，将 node 向左旋转
    child.left = node
    node.right = grand_child
    # 更新结点高度
    self.__update_height(node)
    self.__update_height(child)
    # 返回旋转后子树的根结点
    return child

avl_tree.go

/* 左旋操作 */
func (t *aVLTree) leftRotate(node *TreeNode) *TreeNode {
    child := node.Right
    grandChild := child.Left
    // 以 child 为原点，将 node 向左旋转
    child.Left = node
    node.Right = grandChild
    // 更新结点高度
    t.updateHeight(node)
    t.updateHeight(child)
    // 返回旋转后子树的根结点
    return child
}

avl_tree.js

/* 左旋操作 */
#leftRotate(node) {
    const child = node.right;
    const grandChild = child.left;
    // 以 child 为原点，将 node 向左旋转
    child.left = node;
    node.right = grandChild;
    // 更新结点高度
    this.#updateHeight(node);
    this.#updateHeight(child);
    // 返回旋转后子树的根结点
    return child;
}

avl_tree.ts

/* 左旋操作 */
leftRotate(node: TreeNode): TreeNode {
    const child = node.right;
    const grandChild = child.left;
    // 以 child 为原点，将 node 向左旋转
    child.left = node;
    node.right = grandChild;
    // 更新结点高度
    this.updateHeight(node);
    this.updateHeight(child);
    // 返回旋转后子树的根结点
    return child;
}

avl_tree.c

[class]{aVLTree}-[func]{leftRotate}

avl_tree.cs

/* 左旋操作 */
TreeNode? leftRotate(TreeNode? node)
{
    TreeNode? child = node.right;
    TreeNode? grandChild = child?.left;
    // 以 child 为原点，将 node 向左旋转
    child.left = node;
    node.right = grandChild;
    // 更新结点高度
    updateHeight(node);
    updateHeight(child);
    // 返回旋转后子树的根结点
    return child;
}

avl_tree.swift

/* 左旋操作 */
func leftRotate(node: TreeNode?) -> TreeNode? {
    let child = node?.right
    let grandChild = child?.left
    // 以 child 为原点，将 node 向左旋转
    child?.left = node
    node?.right = grandChild
    // 更新结点高度
    updateHeight(node: node)
    updateHeight(node: child)
    // 返回旋转后子树的根结点
    return child
}

avl_tree.zig

// 左旋操作
fn leftRotate(self: *Self, node: ?*inc.TreeNode(T)) ?*inc.TreeNode(T) {
    var child = node.?.right;
    var grandChild = child.?.left;
    // 以 child 为原点，将 node 向左旋转
    child.?.left = node;
    node.?.right = grandChild;
    // 更新结点高度
    self.updateHeight(node);
    self.updateHeight(child);
    // 返回旋转后子树的根结点
    return child;
}

Case 3 - 先左后右¶

对于下图的失衡结点 3 ，单一使用左旋或右旋都无法使子树恢复平衡，此时需要「先左旋后右旋」，即先对 child 执行「左旋」，再对 node 执行「右旋」。

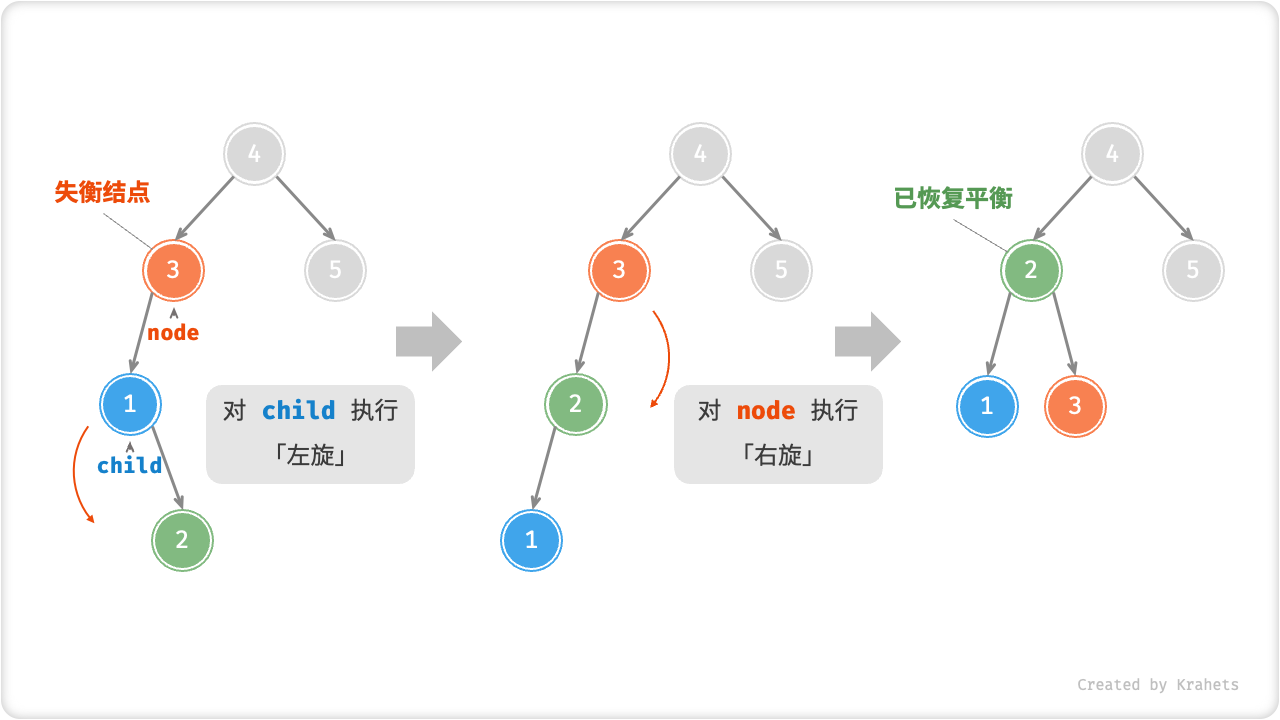
先左旋后右旋

Fig. 先左旋后右旋

Case 4 - 先右后左¶

同理，取以上失衡二叉树的镜像，则需要「先右旋后左旋」，即先对 child 执行「右旋」，然后对 node 执行「左旋」。

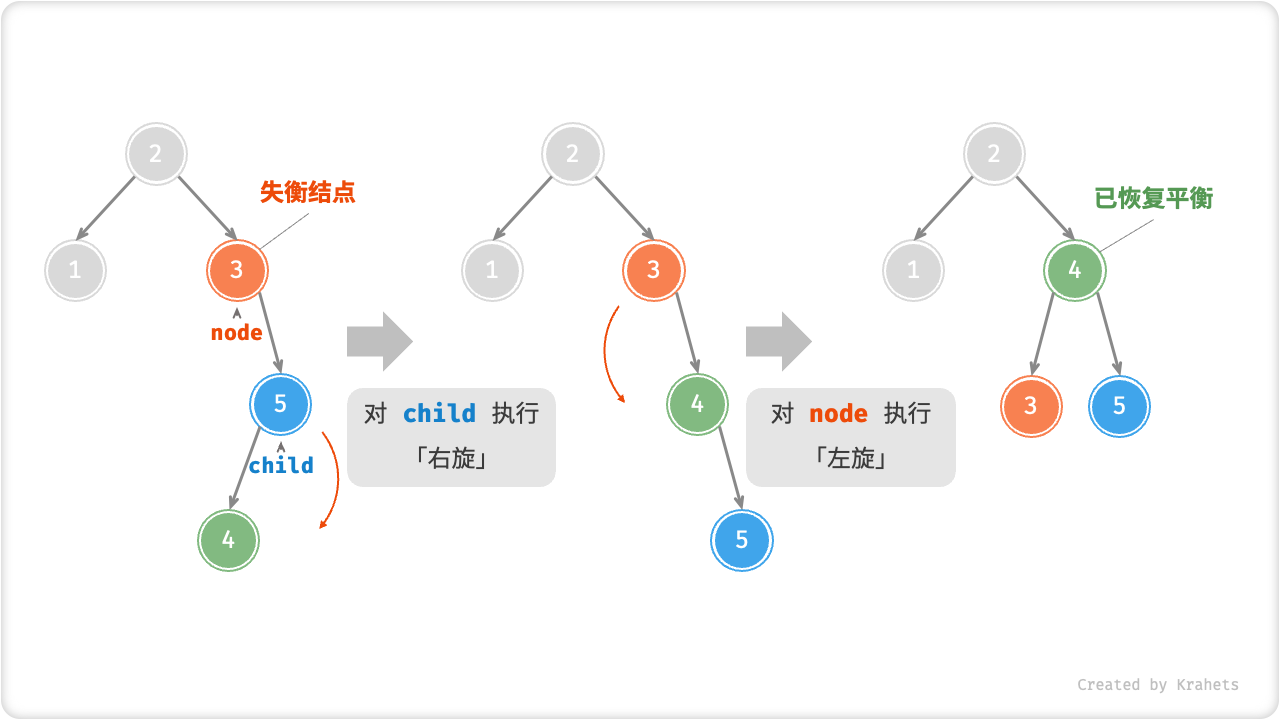
先右旋后左旋

Fig. 先右旋后左旋

旋转的选择¶

下图描述的四种失衡情况与上述 Cases 逐个对应，分别需采用 右旋、左旋、先右后左、先左后右 的旋转操作。

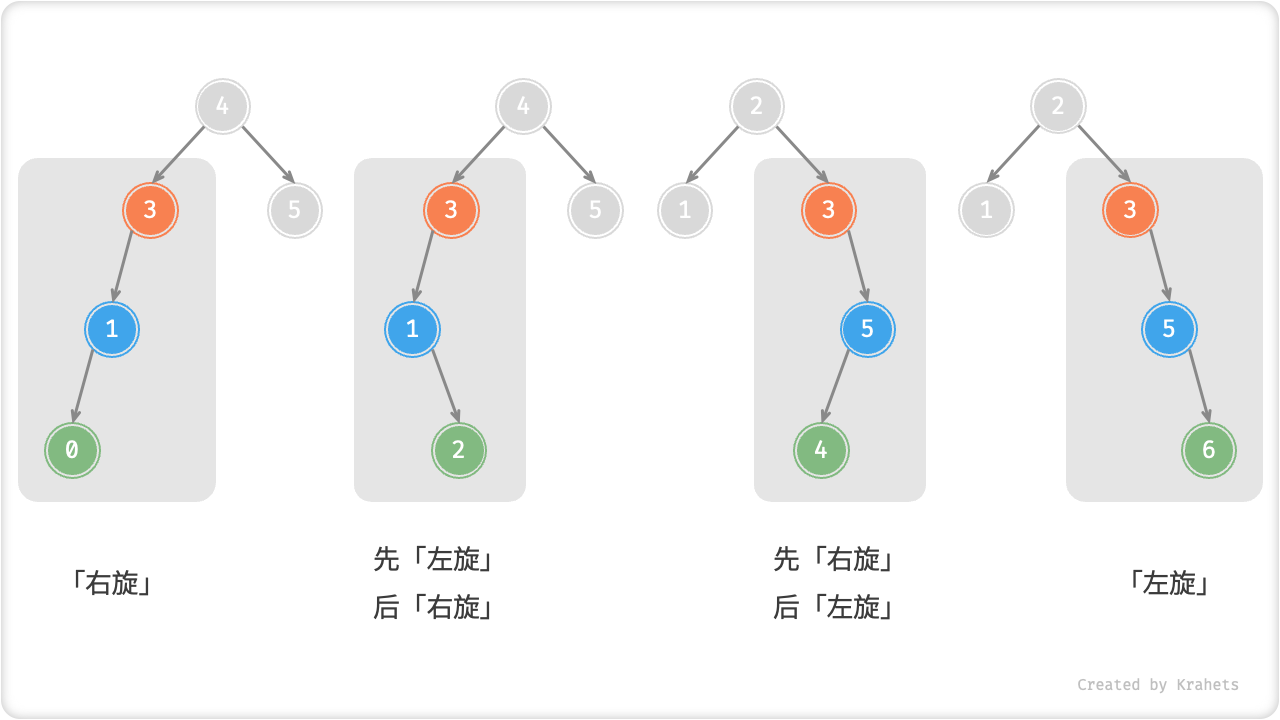
AVL 树的四种旋转情况

Fig. AVL 树的四种旋转情况

具体地，在代码中使用 失衡结点的平衡因子、较高一侧子结点的平衡因子 来确定失衡结点属于上图中的哪种情况。

失衡结点的平衡因子	子结点的平衡因子	应采用的旋转方法
\(>0\) （即左偏树）	\(\geq 0\)	右旋
\(>0\) （即左偏树）	\(<0\)	先左旋后右旋
\(<0\) （即右偏树）	\(\leq 0\)	左旋
\(<0\) （即右偏树）	\(>0\)	先右旋后左旋

为方便使用，我们将旋转操作封装成一个函数。至此，我们可以使用此函数来旋转各种失衡情况，使失衡结点重新恢复平衡。

JavaC++PythonGoJavaScriptTypeScriptCC#SwiftZig

avl_tree.java

/* 执行旋转操作，使该子树重新恢复平衡 */
TreeNode rotate(TreeNode node) {
    // 获取结点 node 的平衡因子
    int balanceFactor = balanceFactor(node);
    // 左偏树
    if (balanceFactor > 1) {
        if (balanceFactor(node.left) >= 0) {
            // 右旋
            return rightRotate(node);
        } else {
            // 先左旋后右旋
            node.left = leftRotate(node.left);
            return rightRotate(node);
        }
    }
    // 右偏树
    if (balanceFactor < -1) {
        if (balanceFactor(node.right) <= 0) {
            // 左旋
            return leftRotate(node);
        } else {
            // 先右旋后左旋
            node.right = rightRotate(node.right);
            return leftRotate(node);
        }
    }
    // 平衡树，无需旋转，直接返回
    return node;
}

avl_tree.cpp

/* 执行旋转操作，使该子树重新恢复平衡 */
TreeNode* rotate(TreeNode* node) {
    // 获取结点 node 的平衡因子
    int _balanceFactor = balanceFactor(node);
    // 左偏树
    if (_balanceFactor > 1) {
        if (balanceFactor(node->left) >= 0) {
            // 右旋
            return rightRotate(node);
        } else {
            // 先左旋后右旋
            node->left = leftRotate(node->left);
            return rightRotate(node);
        }
    }
    // 右偏树
    if (_balanceFactor < -1) {
        if (balanceFactor(node->right) <= 0) {
            // 左旋
            return leftRotate(node);
        } else {
            // 先右旋后左旋
            node->right = rightRotate(node->right);
            return leftRotate(node);
        }
    }
    // 平衡树，无需旋转，直接返回
    return node;
}

avl_tree.py

def __rotate(self, node: TreeNode | None) -> TreeNode | None:
    """ 执行旋转操作，使该子树重新恢复平衡 """
    # 获取结点 node 的平衡因子
    balance_factor = self.balance_factor(node)
    # 左偏树
    if balance_factor > 1:
        if self.balance_factor(node.left) >= 0:
            # 右旋
            return self.__right_rotate(node)
        else:
            # 先左旋后右旋
            node.left = self.__left_rotate(node.left)
            return self.__right_rotate(node)
    # 右偏树
    elif balance_factor < -1:
        if self.balance_factor(node.right) <= 0:
            # 左旋
            return self.__left_rotate(node)
        else:
            # 先右旋后左旋
            node.right = self.__right_rotate(node.right)
            return self.__left_rotate(node)
    # 平衡树，无需旋转，直接返回
    return node

avl_tree.go

/* 执行旋转操作，使该子树重新恢复平衡 */
func (t *aVLTree) rotate(node *TreeNode) *TreeNode {
    // 获取结点 node 的平衡因子
    // Go 推荐短变量，这里 bf 指代 t.balanceFactor
    bf := t.balanceFactor(node)
    // 左偏树
    if bf > 1 {
        if t.balanceFactor(node.Left) >= 0 {
            // 右旋
            return t.rightRotate(node)
        } else {
            // 先左旋后右旋
            node.Left = t.leftRotate(node.Left)
            return t.rightRotate(node)
        }
    }
    // 右偏树
    if bf < -1 {
        if t.balanceFactor(node.Right) <= 0 {
            // 左旋
            return t.leftRotate(node)
        } else {
            // 先右旋后左旋
            node.Right = t.rightRotate(node.Right)
            return t.leftRotate(node)
        }
    }
    // 平衡树，无需旋转，直接返回
    return node
}

avl_tree.js

/* 执行旋转操作，使该子树重新恢复平衡 */
#rotate(node) {
    // 获取结点 node 的平衡因子
    const balanceFactor = this.balanceFactor(node);
    // 左偏树
    if (balanceFactor > 1) {
        if (this.balanceFactor(node.left) >= 0) {
            // 右旋
            return this.#rightRotate(node);
        } else {
            // 先左旋后右旋
            node.left = this.#leftRotate(node.left);
            return this.#rightRotate(node);
        }
    }
    // 右偏树
    if (balanceFactor < -1) {
        if (this.balanceFactor(node.right) <= 0) {
            // 左旋
            return this.#leftRotate(node);
        } else {
            // 先右旋后左旋
            node.right = this.#rightRotate(node.right);
            return this.#leftRotate(node);
        }
    }
    // 平衡树，无需旋转，直接返回
    return node;
}

avl_tree.ts

/* 执行旋转操作，使该子树重新恢复平衡 */
rotate(node: TreeNode): TreeNode {
    // 获取结点 node 的平衡因子
    const balanceFactor = this.balanceFactor(node);
    // 左偏树
    if (balanceFactor > 1) {
        if (this.balanceFactor(node.left) >= 0) {
            // 右旋
            return this.rightRotate(node);
        } else {
            // 先左旋后右旋
            node.left = this.leftRotate(node.left);
            return this.rightRotate(node);
        }
    }
    // 右偏树
    if (balanceFactor < -1) {
        if (this.balanceFactor(node.right) <= 0) {
            // 左旋
            return this.leftRotate(node);
        } else {
            // 先右旋后左旋
            node.right = this.rightRotate(node.right);
            return this.leftRotate(node);
        }
    }
    // 平衡树，无需旋转，直接返回
    return node;
}

avl_tree.c

[class]{aVLTree}-[func]{rotate}

avl_tree.cs

/* 执行旋转操作，使该子树重新恢复平衡 */
TreeNode? rotate(TreeNode? node)
{
    // 获取结点 node 的平衡因子
    int balanceFactorInt = balanceFactor(node);
    // 左偏树
    if (balanceFactorInt > 1)
    {
        if (balanceFactor(node.left) >= 0)
        {
            // 右旋
            return rightRotate(node);
        }
        else
        {
            // 先左旋后右旋
            node.left = leftRotate(node?.left);
            return rightRotate(node);
        }
    }
    // 右偏树
    if (balanceFactorInt < -1)
    {
        if (balanceFactor(node.right) <= 0)
        {
            // 左旋
            return leftRotate(node);
        }
        else
        {
            // 先右旋后左旋
            node.right = rightRotate(node?.right);
            return leftRotate(node);
        }
    }
    // 平衡树，无需旋转，直接返回
    return node;
}

avl_tree.swift

/* 执行旋转操作，使该子树重新恢复平衡 */
func rotate(node: TreeNode?) -> TreeNode? {
    // 获取结点 node 的平衡因子
    let balanceFactor = balanceFactor(node: node)
    // 左偏树
    if balanceFactor > 1 {
        if self.balanceFactor(node: node?.left) >= 0 {
            // 右旋
            return rightRotate(node: node)
        } else {
            // 先左旋后右旋
            node?.left = leftRotate(node: node?.left)
            return rightRotate(node: node)
        }
    }
    // 右偏树
    if balanceFactor < -1 {
        if self.balanceFactor(node: node?.right) <= 0 {
            // 左旋
            return leftRotate(node: node)
        } else {
            // 先右旋后左旋
            node?.right = rightRotate(node: node?.right)
            return leftRotate(node: node)
        }
    }
    // 平衡树，无需旋转，直接返回
    return node
}

avl_tree.zig

// 执行旋转操作，使该子树重新恢复平衡
fn rotate(self: *Self, node: ?*inc.TreeNode(T)) ?*inc.TreeNode(T) {
    // 获取结点 node 的平衡因子
    var balance_factor = self.balanceFactor(node);
    // 左偏树
    if (balance_factor > 1) {
        if (self.balanceFactor(node.?.left) >= 0) {
            // 右旋
            return self.rightRotate(node);
        } else {
            // 先左旋后右旋
            node.?.left = self.leftRotate(node.?.left);
            return self.rightRotate(node);
        }
    }
    // 右偏树
    if (balance_factor < -1) {
        if (self.balanceFactor(node.?.right) <= 0) {
            // 左旋
            return self.leftRotate(node);
        } else {
            // 先右旋后左旋
            node.?.right = self.rightRotate(node.?.right);
            return self.leftRotate(node);
        }
    }
    // 平衡树，无需旋转，直接返回
    return node;
}

7.4.3. AVL 树常用操作¶

插入结点¶

「AVL 树」的结点插入操作与「二叉搜索树」主体类似。不同的是，在插入结点后，从该结点到根结点的路径上会出现一系列「失衡结点」。所以，我们需要从该结点开始，从底至顶地执行旋转操作，使所有失衡结点恢复平衡。

JavaC++PythonGoJavaScriptTypeScriptCC#SwiftZig

avl_tree.java

/* 插入结点 */
TreeNode insert(int val) {
    root = insertHelper(root, val);
    return root;
}

/* 递归插入结点（辅助方法） */
TreeNode insertHelper(TreeNode node, int val) {
    if (node == null) return new TreeNode(val);
    /* 1. 查找插入位置，并插入结点 */
    if (val < node.val)
        node.left = insertHelper(node.left, val);
    else if (val > node.val)
        node.right = insertHelper(node.right, val);
    else
        return node;     // 重复结点不插入，直接返回
    updateHeight(node);  // 更新结点高度
    /* 2. 执行旋转操作，使该子树重新恢复平衡 */
    node = rotate(node);
    // 返回子树的根结点
    return node;
}

avl_tree.cpp

/* 插入结点 */
TreeNode* insert(int val) {
    root = insertHelper(root, val);
    return root;
}

/* 递归插入结点（辅助方法） */
TreeNode* insertHelper(TreeNode* node, int val) {
    if (node == nullptr)
        return new TreeNode(val);
    /* 1. 查找插入位置，并插入结点 */
    if (val < node->val)
        node->left = insertHelper(node->left, val);
    else if (val > node->val)
        node->right = insertHelper(node->right, val);
    else
        return node;     // 重复结点不插入，直接返回
    updateHeight(node);  // 更新结点高度
    /* 2. 执行旋转操作，使该子树重新恢复平衡 */
    node = rotate(node);
    // 返回子树的根结点
    return node;
}

avl_tree.py

def insert(self, val) -> TreeNode:
    """ 插入结点 """
    self.__root = self.__insert_helper(self.__root, val)
    return self.__root

def __insert_helper(self, node: TreeNode | None, val: int) -> TreeNode:
    """ 递归插入结点（辅助方法）"""
    if node is None:
        return TreeNode(val)
    # 1. 查找插入位置，并插入结点
    if val < node.val:
        node.left = self.__insert_helper(node.left, val)
    elif val > node.val:
        node.right = self.__insert_helper(node.right, val)
    else:
        # 重复结点不插入，直接返回
        return node
    # 更新结点高度
    self.__update_height(node)
    # 2. 执行旋转操作，使该子树重新恢复平衡
    return self.__rotate(node)

avl_tree.go

/* 插入结点 */
func (t *aVLTree) insert(val int) *TreeNode {
    t.root = t.insertHelper(t.root, val)
    return t.root
}

/* 递归插入结点（辅助方法） */
func (t *aVLTree) insertHelper(node *TreeNode, val int) *TreeNode {
    if node == nil {
        return NewTreeNode(val)
    }
    /* 1. 查找插入位置，并插入结点 */
    if val < node.Val {
        node.Left = t.insertHelper(node.Left, val)
    } else if val > node.Val {
        node.Right = t.insertHelper(node.Right, val)
    } else {
        // 重复结点不插入，直接返回
        return node
    }
    // 更新结点高度
    t.updateHeight(node)
    /* 2. 执行旋转操作，使该子树重新恢复平衡 */
    node = t.rotate(node)
    // 返回子树的根结点
    return node
}

avl_tree.js

/* 插入结点 */
insert(val) {
    this.root = this.#insertHelper(this.root, val);
    return this.root;
}

/* 递归插入结点（辅助方法） */
#insertHelper(node, val) {
    if (node === null) return new TreeNode(val);
    /* 1. 查找插入位置，并插入结点 */
    if (val < node.val) node.left = this.#insertHelper(node.left, val);
    else if (val > node.val) node.right = this.#insertHelper(node.right, val);
    else return node; // 重复结点不插入，直接返回
    this.#updateHeight(node); // 更新结点高度
    /* 2. 执行旋转操作，使该子树重新恢复平衡 */
    node = this.#rotate(node);
    // 返回子树的根结点
    return node;
}

avl_tree.ts

/* 插入结点 */
insert(val: number): TreeNode {
    this.root = this.insertHelper(this.root, val);
    return this.root;
}

/* 递归插入结点（辅助方法） */
insertHelper(node: TreeNode, val: number): TreeNode {
    if (node === null) return new TreeNode(val);
    /* 1. 查找插入位置，并插入结点 */
    if (val < node.val) {
        node.left = this.insertHelper(node.left, val);
    } else if (val > node.val) {
        node.right = this.insertHelper(node.right, val);
    } else {
        return node; // 重复结点不插入，直接返回
    }
    this.updateHeight(node); // 更新结点高度
    /* 2. 执行旋转操作，使该子树重新恢复平衡 */
    node = this.rotate(node);
    // 返回子树的根结点
    return node;
}

avl_tree.c

[class]{aVLTree}-[func]{insert}

[class]{aVLTree}-[func]{insertHelper}

avl_tree.cs

/* 插入结点 */
TreeNode? insert(int val)
{
    root = insertHelper(root, val);
    return root;
}

/* 递归插入结点（辅助方法） */
TreeNode? insertHelper(TreeNode? node, int val)
{
    if (node == null) return new TreeNode(val);
    /* 1. 查找插入位置，并插入结点 */
    if (val < node.val)
        node.left = insertHelper(node.left, val);
    else if (val > node.val)
        node.right = insertHelper(node.right, val);
    else
        return node;     // 重复结点不插入，直接返回
    updateHeight(node);  // 更新结点高度
    /* 2. 执行旋转操作，使该子树重新恢复平衡 */
    node = rotate(node);
    // 返回子树的根结点
    return node;
}

avl_tree.swift

/* 插入结点 */
@discardableResult
func insert(val: Int) -> TreeNode? {
    root = insertHelper(node: root, val: val)
    return root
}

/* 递归插入结点（辅助方法） */
func insertHelper(node: TreeNode?, val: Int) -> TreeNode? {
    var node = node
    if node == nil {
        return TreeNode(x: val)
    }
    /* 1. 查找插入位置，并插入结点 */
    if val < node!.val {
        node?.left = insertHelper(node: node?.left, val: val)
    } else if val > node!.val {
        node?.right = insertHelper(node: node?.right, val: val)
    } else {
        return node // 重复结点不插入，直接返回
    }
    updateHeight(node: node) // 更新结点高度
    /* 2. 执行旋转操作，使该子树重新恢复平衡 */
    node = rotate(node: node)
    // 返回子树的根结点
    return node
}

avl_tree.zig

// 插入结点
fn insert(self: *Self, val: T) !?*inc.TreeNode(T) {
    self.root = try self.insertHelper(self.root, val);
    return self.root;
}

// 递归插入结点（辅助方法）
fn insertHelper(self: *Self, node_: ?*inc.TreeNode(T), val: T) !?*inc.TreeNode(T) {
    var node = node_;
    if (node == null) {
        var tmp_node = try self.mem_allocator.create(inc.TreeNode(T));
        tmp_node.init(val);
        return tmp_node;
    }
    // 1. 查找插入位置，并插入结点
    if (val < node.?.val) {
        node.?.left = try self.insertHelper(node.?.left, val);
    } else if (val > node.?.val) {
        node.?.right = try self.insertHelper(node.?.right, val);
    } else {
        return node;            // 重复结点不插入，直接返回
    }
    self.updateHeight(node);    // 更新结点高度
    // 2. 执行旋转操作，使该子树重新恢复平衡
    node = self.rotate(node);
    // 返回子树的根结点
    return node;
}

删除结点¶

「AVL 树」删除结点操作与「二叉搜索树」删除结点操作总体相同。类似地，在删除结点后，也需要从底至顶地执行旋转操作，使所有失衡结点恢复平衡。

JavaC++PythonGoJavaScriptTypeScriptCC#SwiftZig

avl_tree.java

/* 删除结点 */
TreeNode remove(int val) {
    root = removeHelper(root, val);
    return root;
}

/* 递归删除结点（辅助方法） */
TreeNode removeHelper(TreeNode node, int val) {
    if (node == null) return null;
    /* 1. 查找结点，并删除之 */
    if (val < node.val)
        node.left = removeHelper(node.left, val);
    else if (val > node.val)
        node.right = removeHelper(node.right, val);
    else {
        if (node.left == null || node.right == null) {
            TreeNode child = node.left != null ? node.left : node.right;
            // 子结点数量 = 0 ，直接删除 node 并返回
            if (child == null)
                return null;
            // 子结点数量 = 1 ，直接删除 node
            else
                node = child;
        } else {
            // 子结点数量 = 2 ，则将中序遍历的下个结点删除，并用该结点替换当前结点
            TreeNode temp = getInOrderNext(node.right);
            node.right = removeHelper(node.right, temp.val);
            node.val = temp.val;
        }
    }
    updateHeight(node);  // 更新结点高度
    /* 2. 执行旋转操作，使该子树重新恢复平衡 */
    node = rotate(node);
    // 返回子树的根结点
    return node;
}

/* 获取中序遍历中的下一个结点（仅适用于 root 有左子结点的情况） */
TreeNode getInOrderNext(TreeNode node) {
    if (node == null) return node;
    // 循环访问左子结点，直到叶结点时为最小结点，跳出
    while (node.left != null) {
        node = node.left;
    }
    return node;
}

avl_tree.cpp

/* 删除结点 */
TreeNode* remove(int val) {
    root = removeHelper(root, val);
    return root;
}

/* 递归删除结点（辅助方法） */
TreeNode* removeHelper(TreeNode* node, int val) {
    if (node == nullptr)
        return nullptr;
    /* 1. 查找结点，并删除之 */
    if (val < node->val)
        node->left = removeHelper(node->left, val);
    else if (val > node->val)
        node->right = removeHelper(node->right, val);
    else {
        if (node->left == nullptr || node->right == nullptr) {
            TreeNode* child = node->left != nullptr ? node->left : node->right;
            // 子结点数量 = 0 ，直接删除 node 并返回
            if (child == nullptr) {
                delete node;
                return nullptr;
            }
            // 子结点数量 = 1 ，直接删除 node
            else {
                delete node;
                node = child;
            }
        } else {
            // 子结点数量 = 2 ，则将中序遍历的下个结点删除，并用该结点替换当前结点
            TreeNode* temp = getInOrderNext(node->right);
            int tempVal = temp->val;
            node->right = removeHelper(node->right, temp->val);
            node->val = tempVal;
        }
    }
    updateHeight(node);  // 更新结点高度
    /* 2. 执行旋转操作，使该子树重新恢复平衡 */
    node = rotate(node);
    // 返回子树的根结点
    return node;
}

/* 获取中序遍历中的下一个结点（仅适用于 root 有左子结点的情况） */
TreeNode* getInOrderNext(TreeNode* node) {
    if (node == nullptr)
        return node;
    // 循环访问左子结点，直到叶结点时为最小结点，跳出
    while (node->left != nullptr) {
        node = node->left;
    }
    return node;
}

avl_tree.py

def remove(self, val: int) -> TreeNode | None:
    """ 删除结点 """
    self.__root = self.__remove_helper(self.__root, val)
    return self.__root 

def __remove_helper(self, node: TreeNode | None, val: int) -> TreeNode | None:
    """ 递归删除结点（辅助方法） """
    if node is None:
        return None
    # 1. 查找结点，并删除之
    if val < node.val:
        node.left = self.__remove_helper(node.left, val)
    elif val > node.val:
        node.right = self.__remove_helper(node.right, val)
    else:
        if node.left is None or node.right is None:
            child = node.left or node.right
            # 子结点数量 = 0 ，直接删除 node 并返回
            if child is None:
                return None
            # 子结点数量 = 1 ，直接删除 node
            else:
                node = child
        else:  # 子结点数量 = 2 ，则将中序遍历的下个结点删除，并用该结点替换当前结点
            temp = self.__get_inorder_next(node.right)
            node.right = self.__remove_helper(node.right, temp.val)
            node.val = temp.val
    # 更新结点高度
    self.__update_height(node)
    # 2. 执行旋转操作，使该子树重新恢复平衡
    return self.__rotate(node)

def __get_inorder_next(self, node: TreeNode | None) -> TreeNode | None:
    """ 获取中序遍历中的下一个结点（仅适用于 root 有左子结点的情况） """
    if node is None:
        return None
    # 循环访问左子结点，直到叶结点时为最小结点，跳出
    while node.left is not None:
        node = node.left
    return node

avl_tree.go

/* 删除结点 */
func (t *aVLTree) remove(val int) *TreeNode {
    root := t.removeHelper(t.root, val)
    return root
}

/* 递归删除结点（辅助方法） */
func (t *aVLTree) removeHelper(node *TreeNode, val int) *TreeNode {
    if node == nil {
        return nil
    }
    /* 1. 查找结点，并删除之 */
    if val < node.Val {
        node.Left = t.removeHelper(node.Left, val)
    } else if val > node.Val {
        node.Right = t.removeHelper(node.Right, val)
    } else {
        if node.Left == nil || node.Right == nil {
            child := node.Left
            if node.Right != nil {
                child = node.Right
            }
            // 子结点数量 = 0 ，直接删除 node 并返回
            if child == nil {
                return nil
            } else {
                // 子结点数量 = 1 ，直接删除 node
                node = child
            }
        } else {
            // 子结点数量 = 2 ，则将中序遍历的下个结点删除，并用该结点替换当前结点
            temp := t.getInOrderNext(node.Right)
            node.Right = t.removeHelper(node.Right, temp.Val)
            node.Val = temp.Val
        }
    }
    // 更新结点高度
    t.updateHeight(node)
    /* 2. 执行旋转操作，使该子树重新恢复平衡 */
    node = t.rotate(node)
    // 返回子树的根结点
    return node
}

/* 获取中序遍历中的下一个结点（仅适用于 root 有左子结点的情况） */
func (t *aVLTree) getInOrderNext(node *TreeNode) *TreeNode {
    if node == nil {
        return node
    }
    // 循环访问左子结点，直到叶结点时为最小结点，跳出
    for node.Left != nil {
        node = node.Left
    }
    return node
}

avl_tree.js

/* 删除结点 */
remove(val) {
    this.root = this.#removeHelper(this.root, val);
    return this.root;
}

/* 递归删除结点（辅助方法） */
#removeHelper(node, val) {
    if (node === null) return null;
    /* 1. 查找结点，并删除之 */
    if (val < node.val) node.left = this.#removeHelper(node.left, val);
    else if (val > node.val) node.right = this.#removeHelper(node.right, val);
    else {
        if (node.left === null || node.right === null) {
            const child = node.left !== null ? node.left : node.right;
            // 子结点数量 = 0 ，直接删除 node 并返回
            if (child === null) return null;
            // 子结点数量 = 1 ，直接删除 node
            else node = child;
        } else {
            // 子结点数量 = 2 ，则将中序遍历的下个结点删除，并用该结点替换当前结点
            const temp = this.#getInOrderNext(node.right);
            node.right = this.#removeHelper(node.right, temp.val);
            node.val = temp.val;
        }
    }
    this.#updateHeight(node); // 更新结点高度
    /* 2. 执行旋转操作，使该子树重新恢复平衡 */
    node = this.#rotate(node);
    // 返回子树的根结点
    return node;
}

/* 获取中序遍历中的下一个结点（仅适用于 root 有左子结点的情况） */
#getInOrderNext(node) {
    if (node === null) return node;
    // 循环访问左子结点，直到叶结点时为最小结点，跳出
    while (node.left !== null) {
        node = node.left;
    }
    return node;
}

avl_tree.ts

/* 删除结点 */
remove(val: number): TreeNode {
    this.root = this.removeHelper(this.root, val);
    return this.root;
}

/* 递归删除结点（辅助方法） */
removeHelper(node: TreeNode, val: number): TreeNode {
    if (node === null) return null;
    /* 1. 查找结点，并删除之 */
    if (val < node.val) {
        node.left = this.removeHelper(node.left, val);
    } else if (val > node.val) {
        node.right = this.removeHelper(node.right, val);
    } else {
        if (node.left === null || node.right === null) {
            const child = node.left !== null ? node.left : node.right;
            // 子结点数量 = 0 ，直接删除 node 并返回
            if (child === null) {
                return null;
            } else {
                // 子结点数量 = 1 ，直接删除 node
                node = child;
            }
        } else {
            // 子结点数量 = 2 ，则将中序遍历的下个结点删除，并用该结点替换当前结点
            const temp = this.getInOrderNext(node.right);
            node.right = this.removeHelper(node.right, temp.val);
            node.val = temp.val;
        }
    }
    this.updateHeight(node); // 更新结点高度
    /* 2. 执行旋转操作，使该子树重新恢复平衡 */
    node = this.rotate(node);
    // 返回子树的根结点
    return node;
}

/* 获取中序遍历中的下一个结点（仅适用于 root 有左子结点的情况） */
getInOrderNext(node: TreeNode): TreeNode {
    if (node === null) return node;
    // 循环访问左子结点，直到叶结点时为最小结点，跳出
    while (node.left !== null) {
        node = node.left;
    }
    return node;
}

avl_tree.c

[class]{aVLTree}-[func]{remove}

[class]{aVLTree}-[func]{removeHelper}

[class]{aVLTree}-[func]{getInOrderNext}

avl_tree.cs

/* 删除结点 */
TreeNode? remove(int val)
{
    root = removeHelper(root, val);
    return root;
}

/* 递归删除结点（辅助方法） */
TreeNode? removeHelper(TreeNode? node, int val)
{
    if (node == null) return null;
    /* 1. 查找结点，并删除之 */
    if (val < node.val)
        node.left = removeHelper(node.left, val);
    else if (val > node.val)
        node.right = removeHelper(node.right, val);
    else
    {
        if (node.left == null || node.right == null)
        {
            TreeNode? child = node.left != null ? node.left : node.right;
            // 子结点数量 = 0 ，直接删除 node 并返回
            if (child == null)
                return null;
            // 子结点数量 = 1 ，直接删除 node
            else
                node = child;
        }
        else
        {
            // 子结点数量 = 2 ，则将中序遍历的下个结点删除，并用该结点替换当前结点
            TreeNode? temp = getInOrderNext(node.right);
            node.right = removeHelper(node.right, temp.val);
            node.val = temp.val;
        }
    }
    updateHeight(node);  // 更新结点高度
    /* 2. 执行旋转操作，使该子树重新恢复平衡 */
    node = rotate(node);
    // 返回子树的根结点
    return node;
}

/* 获取中序遍历中的下一个结点（仅适用于 root 有左子结点的情况） */
TreeNode? getInOrderNext(TreeNode? node)
{
    if (node == null) return node;
    // 循环访问左子结点，直到叶结点时为最小结点，跳出
    while (node.left != null)
    {
        node = node.left;
    }
    return node;
}

avl_tree.swift

/* 删除结点 */
@discardableResult
func remove(val: Int) -> TreeNode? {
    root = removeHelper(node: root, val: val)
    return root
}

/* 递归删除结点（辅助方法） */
func removeHelper(node: TreeNode?, val: Int) -> TreeNode? {
    var node = node
    if node == nil {
        return nil
    }
    /* 1. 查找结点，并删除之 */
    if val < node!.val {
        node?.left = removeHelper(node: node?.left, val: val)
    } else if val > node!.val {
        node?.right = removeHelper(node: node?.right, val: val)
    } else {
        if node?.left == nil || node?.right == nil {
            let child = node?.left != nil ? node?.left : node?.right
            // 子结点数量 = 0 ，直接删除 node 并返回
            if child == nil {
                return nil
            }
            // 子结点数量 = 1 ，直接删除 node
            else {
                node = child
            }
        } else {
            // 子结点数量 = 2 ，则将中序遍历的下个结点删除，并用该结点替换当前结点
            let temp = getInOrderNext(node: node?.right)
            node?.right = removeHelper(node: node?.right, val: temp!.val)
            node?.val = temp!.val
        }
    }
    updateHeight(node: node) // 更新结点高度
    /* 2. 执行旋转操作，使该子树重新恢复平衡 */
    node = rotate(node: node)
    // 返回子树的根结点
    return node
}

/* 获取中序遍历中的下一个结点（仅适用于 root 有左子结点的情况） */
func getInOrderNext(node: TreeNode?) -> TreeNode? {
    var node = node
    if node == nil {
        return node
    }
    // 循环访问左子结点，直到叶结点时为最小结点，跳出
    while node?.left != nil {
        node = node?.left
    }
    return node
}

avl_tree.zig

// 删除结点
fn remove(self: *Self, val: T) ?*inc.TreeNode(T) {
   self.root = self.removeHelper(self.root, val);
    return self.root;
}

// 递归删除结点（辅助方法）
fn removeHelper(self: *Self, node_: ?*inc.TreeNode(T), val: T) ?*inc.TreeNode(T) {
    var node = node_;
    if (node == null) return null;
    // 1. 查找结点，并删除之
    if (val < node.?.val) {
        node.?.left = self.removeHelper(node.?.left, val);
    } else if (val > node.?.val) {
        node.?.right = self.removeHelper(node.?.right, val);
    } else {
        if (node.?.left == null or node.?.right == null) {
            var child = if (node.?.left != null) node.?.left else node.?.right;
            // 子结点数量 = 0 ，直接删除 node 并返回
            if (child == null) {
                return null;
            // 子结点数量 = 1 ，直接删除 node
            } else {
                node = child;
            }
        } else {
            // 子结点数量 = 2 ，则将中序遍历的下个结点删除，并用该结点替换当前结点
            var temp = self.getInOrderNext(node.?.right);
            node.?.right = self.removeHelper(node.?.right, temp.?.val);
            node.?.val = temp.?.val;
        }
    }
    self.updateHeight(node);    // 更新结点高度
    // 2. 执行旋转操作，使该子树重新恢复平衡
    node = self.rotate(node);
    // 返回子树的根结点
    return node;
}

// 获取中序遍历中的下一个结点（仅适用于 root 有左子结点的情况）
fn getInOrderNext(self: *Self, node_: ?*inc.TreeNode(T)) ?*inc.TreeNode(T) {
    _ = self;
    var node = node_;
    if (node == null) return node;
    // 循环访问左子结点，直到叶结点时为最小结点，跳出
    while (node.?.left != null) {
        node = node.?.left;
    }
    return node;
}

查找结点¶

「AVL 树」的结点查找操作与「二叉搜索树」一致，在此不再赘述。

7.4.4. AVL 树典型应用¶

组织存储大型数据，适用于高频查找、低频增删场景；
用于建立数据库中的索引系统；

为什么红黑树比 AVL 树更受欢迎？

红黑树的平衡条件相对宽松，因此在红黑树中插入与删除结点所需的旋转操作相对更少，结点增删操作相比 AVL 树的效率更高。

7.4. AVL 树 *¶

7.4.1. AVL 树常见术语¶

结点高度¶

结点平衡因子¶

7.4.2. AVL 树旋转¶

Case 1 - 右旋¶

Case 2 - 左旋¶

Case 3 - 先左后右¶

Case 4 - 先右后左¶

旋转的选择¶

7.4.3. AVL 树常用操作¶

插入结点¶

删除结点¶

查找结点¶

7.4.4. AVL 树典型应用¶

评论