13.3   子集和問題

13.3.1   無重複元素的情況

Question

給定一個正整數陣列 nums 和一個目標正整數 target ，請找出所有可能的組合，使得組合中的元素和等於 target 。給定陣列無重複元素，每個元素可以被選取多次。請以串列形式返回這些組合，串列中不應包含重複組合。

例如，輸入集合 \(\{3, 4, 5\}\) 和目標整數 \(9\) ，解為 \(\{3, 3, 3\}, \{4, 5\}\) 。需要注意以下兩點。

• 輸入集合中的元素可以被無限次重複選取。
• 子集不區分元素順序，比如 \(\{4, 5\}\) 和 \(\{5, 4\}\) 是同一個子集。

1.   參考全排列解法

類似於全排列問題，我們可以把子集的生成過程想象成一系列選擇的結果，並在選擇過程中實時更新“元素和”，當元素和等於 target 時，就將子集記錄至結果串列。

而與全排列問題不同的是，本題集合中的元素可以被無限次選取，因此無須藉助 selected 布林串列來記錄元素是否已被選擇。我們可以對全排列程式碼進行小幅修改，初步得到解題程式碼：

PythonC++JavaC#GoSwiftJSTSDartRustCKotlinRubyZig

subset_sum_i_naive.py

def backtrack(
    state: list[int],
    target: int,
    total: int,
    choices: list[int],
    res: list[list[int]],
):
    """回溯演算法：子集和 I"""
    # 子集和等於 target 時，記錄解
    if total == target:
        res.append(list(state))
        return
    # 走訪所有選擇
    for i in range(len(choices)):
        # 剪枝：若子集和超過 target ，則跳過該選擇
        if total + choices[i] > target:
            continue
        # 嘗試：做出選擇，更新元素和 total
        state.append(choices[i])
        # 進行下一輪選擇
        backtrack(state, target, total + choices[i], choices, res)
        # 回退：撤銷選擇，恢復到之前的狀態
        state.pop()

def subset_sum_i_naive(nums: list[int], target: int) -> list[list[int]]:
    """求解子集和 I（包含重複子集）"""
    state = []  # 狀態（子集）
    total = 0  # 子集和
    res = []  # 結果串列（子集串列）
    backtrack(state, target, total, nums, res)
    return res

subset_sum_i_naive.cpp

/* 回溯演算法：子集和 I */
void backtrack(vector<int> &state, int target, int total, vector<int> &choices, vector<vector<int>> &res) {
    // 子集和等於 target 時，記錄解
    if (total == target) {
        res.push_back(state);
        return;
    }
    // 走訪所有選擇
    for (size_t i = 0; i < choices.size(); i++) {
        // 剪枝：若子集和超過 target ，則跳過該選擇
        if (total + choices[i] > target) {
            continue;
        }
        // 嘗試：做出選擇，更新元素和 total
        state.push_back(choices[i]);
        // 進行下一輪選擇
        backtrack(state, target, total + choices[i], choices, res);
        // 回退：撤銷選擇，恢復到之前的狀態
        state.pop_back();
    }
}

/* 求解子集和 I（包含重複子集） */
vector<vector<int>> subsetSumINaive(vector<int> &nums, int target) {
    vector<int> state;       // 狀態（子集）
    int total = 0;           // 子集和
    vector<vector<int>> res; // 結果串列（子集串列）
    backtrack(state, target, total, nums, res);
    return res;
}

subset_sum_i_naive.java

/* 回溯演算法：子集和 I */
void backtrack(List<Integer> state, int target, int total, int[] choices, List<List<Integer>> res) {
    // 子集和等於 target 時，記錄解
    if (total == target) {
        res.add(new ArrayList<>(state));
        return;
    }
    // 走訪所有選擇
    for (int i = 0; i < choices.length; i++) {
        // 剪枝：若子集和超過 target ，則跳過該選擇
        if (total + choices[i] > target) {
            continue;
        }
        // 嘗試：做出選擇，更新元素和 total
        state.add(choices[i]);
        // 進行下一輪選擇
        backtrack(state, target, total + choices[i], choices, res);
        // 回退：撤銷選擇，恢復到之前的狀態
        state.remove(state.size() - 1);
    }
}

/* 求解子集和 I（包含重複子集） */
List<List<Integer>> subsetSumINaive(int[] nums, int target) {
    List<Integer> state = new ArrayList<>(); // 狀態（子集）
    int total = 0; // 子集和
    List<List<Integer>> res = new ArrayList<>(); // 結果串列（子集串列）
    backtrack(state, target, total, nums, res);
    return res;
}

subset_sum_i_naive.cs

/* 回溯演算法：子集和 I */
void Backtrack(List<int> state, int target, int total, int[] choices, List<List<int>> res) {
    // 子集和等於 target 時，記錄解
    if (total == target) {
        res.Add(new List<int>(state));
        return;
    }
    // 走訪所有選擇
    for (int i = 0; i < choices.Length; i++) {
        // 剪枝：若子集和超過 target ，則跳過該選擇
        if (total + choices[i] > target) {
            continue;
        }
        // 嘗試：做出選擇，更新元素和 total
        state.Add(choices[i]);
        // 進行下一輪選擇
        Backtrack(state, target, total + choices[i], choices, res);
        // 回退：撤銷選擇，恢復到之前的狀態
        state.RemoveAt(state.Count - 1);
    }
}

/* 求解子集和 I（包含重複子集） */
List<List<int>> SubsetSumINaive(int[] nums, int target) {
    List<int> state = []; // 狀態（子集）
    int total = 0; // 子集和
    List<List<int>> res = []; // 結果串列（子集串列）
    Backtrack(state, target, total, nums, res);
    return res;
}

subset_sum_i_naive.go

/* 回溯演算法：子集和 I */
func backtrackSubsetSumINaive(total, target int, state, choices *[]int, res *[][]int) {
    // 子集和等於 target 時，記錄解
    if target == total {
        newState := append([]int{}, *state...)
        *res = append(*res, newState)
        return
    }
    // 走訪所有選擇
    for i := 0; i < len(*choices); i++ {
        // 剪枝：若子集和超過 target ，則跳過該選擇
        if total+(*choices)[i] > target {
            continue
        }
        // 嘗試：做出選擇，更新元素和 total
        *state = append(*state, (*choices)[i])
        // 進行下一輪選擇
        backtrackSubsetSumINaive(total+(*choices)[i], target, state, choices, res)
        // 回退：撤銷選擇，恢復到之前的狀態
        *state = (*state)[:len(*state)-1]
    }
}

/* 求解子集和 I（包含重複子集） */
func subsetSumINaive(nums []int, target int) [][]int {
    state := make([]int, 0) // 狀態（子集）
    total := 0              // 子集和
    res := make([][]int, 0) // 結果串列（子集串列）
    backtrackSubsetSumINaive(total, target, &state, &nums, &res)
    return res
}

subset_sum_i_naive.swift

/* 回溯演算法：子集和 I */
func backtrack(state: inout [Int], target: Int, total: Int, choices: [Int], res: inout [[Int]]) {
    // 子集和等於 target 時，記錄解
    if total == target {
        res.append(state)
        return
    }
    // 走訪所有選擇
    for i in choices.indices {
        // 剪枝：若子集和超過 target ，則跳過該選擇
        if total + choices[i] > target {
            continue
        }
        // 嘗試：做出選擇，更新元素和 total
        state.append(choices[i])
        // 進行下一輪選擇
        backtrack(state: &state, target: target, total: total + choices[i], choices: choices, res: &res)
        // 回退：撤銷選擇，恢復到之前的狀態
        state.removeLast()
    }
}

/* 求解子集和 I（包含重複子集） */
func subsetSumINaive(nums: [Int], target: Int) -> [[Int]] {
    var state: [Int] = [] // 狀態（子集）
    let total = 0 // 子集和
    var res: [[Int]] = [] // 結果串列（子集串列）
    backtrack(state: &state, target: target, total: total, choices: nums, res: &res)
    return res
}

subset_sum_i_naive.js

/* 回溯演算法：子集和 I */
function backtrack(state, target, total, choices, res) {
    // 子集和等於 target 時，記錄解
    if (total === target) {
        res.push([...state]);
        return;
    }
    // 走訪所有選擇
    for (let i = 0; i < choices.length; i++) {
        // 剪枝：若子集和超過 target ，則跳過該選擇
        if (total + choices[i] > target) {
            continue;
        }
        // 嘗試：做出選擇，更新元素和 total
        state.push(choices[i]);
        // 進行下一輪選擇
        backtrack(state, target, total + choices[i], choices, res);
        // 回退：撤銷選擇，恢復到之前的狀態
        state.pop();
    }
}

/* 求解子集和 I（包含重複子集） */
function subsetSumINaive(nums, target) {
    const state = []; // 狀態（子集）
    const total = 0; // 子集和
    const res = []; // 結果串列（子集串列）
    backtrack(state, target, total, nums, res);
    return res;
}

subset_sum_i_naive.ts

/* 回溯演算法：子集和 I */
function backtrack(
    state: number[],
    target: number,
    total: number,
    choices: number[],
    res: number[][]
): void {
    // 子集和等於 target 時，記錄解
    if (total === target) {
        res.push([...state]);
        return;
    }
    // 走訪所有選擇
    for (let i = 0; i < choices.length; i++) {
        // 剪枝：若子集和超過 target ，則跳過該選擇
        if (total + choices[i] > target) {
            continue;
        }
        // 嘗試：做出選擇，更新元素和 total
        state.push(choices[i]);
        // 進行下一輪選擇
        backtrack(state, target, total + choices[i], choices, res);
        // 回退：撤銷選擇，恢復到之前的狀態
        state.pop();
    }
}

/* 求解子集和 I（包含重複子集） */
function subsetSumINaive(nums: number[], target: number): number[][] {
    const state = []; // 狀態（子集）
    const total = 0; // 子集和
    const res = []; // 結果串列（子集串列）
    backtrack(state, target, total, nums, res);
    return res;
}

subset_sum_i_naive.dart

/* 回溯演算法：子集和 I */
void backtrack(
  List<int> state,
  int target,
  int total,
  List<int> choices,
  List<List<int>> res,
) {
  // 子集和等於 target 時，記錄解
  if (total == target) {
    res.add(List.from(state));
    return;
  }
  // 走訪所有選擇
  for (int i = 0; i < choices.length; i++) {
    // 剪枝：若子集和超過 target ，則跳過該選擇
    if (total + choices[i] > target) {
      continue;
    }
    // 嘗試：做出選擇，更新元素和 total
    state.add(choices[i]);
    // 進行下一輪選擇
    backtrack(state, target, total + choices[i], choices, res);
    // 回退：撤銷選擇，恢復到之前的狀態
    state.removeLast();
  }
}

/* 求解子集和 I（包含重複子集） */
List<List<int>> subsetSumINaive(List<int> nums, int target) {
  List<int> state = []; // 狀態（子集）
  int total = 0; // 元素和
  List<List<int>> res = []; // 結果串列（子集串列）
  backtrack(state, target, total, nums, res);
  return res;
}

subset_sum_i_naive.rs

/* 回溯演算法：子集和 I */
fn backtrack(
    mut state: Vec<i32>,
    target: i32,
    total: i32,
    choices: &[i32],
    res: &mut Vec<Vec<i32>>,
) {
    // 子集和等於 target 時，記錄解
    if total == target {
        res.push(state);
        return;
    }
    // 走訪所有選擇
    for i in 0..choices.len() {
        // 剪枝：若子集和超過 target ，則跳過該選擇
        if total + choices[i] > target {
            continue;
        }
        // 嘗試：做出選擇，更新元素和 total
        state.push(choices[i]);
        // 進行下一輪選擇
        backtrack(state.clone(), target, total + choices[i], choices, res);
        // 回退：撤銷選擇，恢復到之前的狀態
        state.pop();
    }
}

/* 求解子集和 I（包含重複子集） */
fn subset_sum_i_naive(nums: &[i32], target: i32) -> Vec<Vec<i32>> {
    let state = Vec::new(); // 狀態（子集）
    let total = 0; // 子集和
    let mut res = Vec::new(); // 結果串列（子集串列）
    backtrack(state, target, total, nums, &mut res);
    res
}

subset_sum_i_naive.c

/* 回溯演算法：子集和 I */
void backtrack(int target, int total, int *choices, int choicesSize) {
    // 子集和等於 target 時，記錄解
    if (total == target) {
        for (int i = 0; i < stateSize; i++) {
            res[resSize][i] = state[i];
        }
        resColSizes[resSize++] = stateSize;
        return;
    }
    // 走訪所有選擇
    for (int i = 0; i < choicesSize; i++) {
        // 剪枝：若子集和超過 target ，則跳過該選擇
        if (total + choices[i] > target) {
            continue;
        }
        // 嘗試：做出選擇，更新元素和 total
        state[stateSize++] = choices[i];
        // 進行下一輪選擇
        backtrack(target, total + choices[i], choices, choicesSize);
        // 回退：撤銷選擇，恢復到之前的狀態
        stateSize--;
    }
}

/* 求解子集和 I（包含重複子集） */
void subsetSumINaive(int *nums, int numsSize, int target) {
    resSize = 0; // 初始化解的數量為0
    backtrack(target, 0, nums, numsSize);
}

subset_sum_i_naive.kt

/* 回溯演算法：子集和 I */
fun backtrack(
    state: MutableList<Int>,
    target: Int,
    total: Int,
    choices: IntArray,
    res: MutableList<MutableList<Int>?>
) {
    // 子集和等於 target 時，記錄解
    if (total == target) {
        res.add(state.toMutableList())
        return
    }
    // 走訪所有選擇
    for (i in choices.indices) {
        // 剪枝：若子集和超過 target ，則跳過該選擇
        if (total + choices[i] > target) {
            continue
        }
        // 嘗試：做出選擇，更新元素和 total
        state.add(choices[i])
        // 進行下一輪選擇
        backtrack(state, target, total + choices[i], choices, res)
        // 回退：撤銷選擇，恢復到之前的狀態
        state.removeAt(state.size - 1)
    }
}

/* 求解子集和 I（包含重複子集） */
fun subsetSumINaive(nums: IntArray, target: Int): MutableList<MutableList<Int>?> {
    val state = mutableListOf<Int>() // 狀態（子集）
    val total = 0 // 子集和
    val res = mutableListOf<MutableList<Int>?>() // 結果串列（子集串列）
    backtrack(state, target, total, nums, res)
    return res
}

subset_sum_i_naive.rb

[class]{}-[func]{backtrack}

[class]{}-[func]{subset_sum_i_naive}

subset_sum_i_naive.zig

[class]{}-[func]{backtrack}

[class]{}-[func]{subsetSumINaive}

視覺化執行

全螢幕觀看 >

向以上程式碼輸入陣列 \([3, 4, 5]\) 和目標元素 \(9\) ，輸出結果為 \([3, 3, 3], [4, 5], [5, 4]\) 。雖然成功找出了所有和為 \(9\) 的子集，但其中存在重複的子集 \([4, 5]\) 和 \([5, 4]\) 。

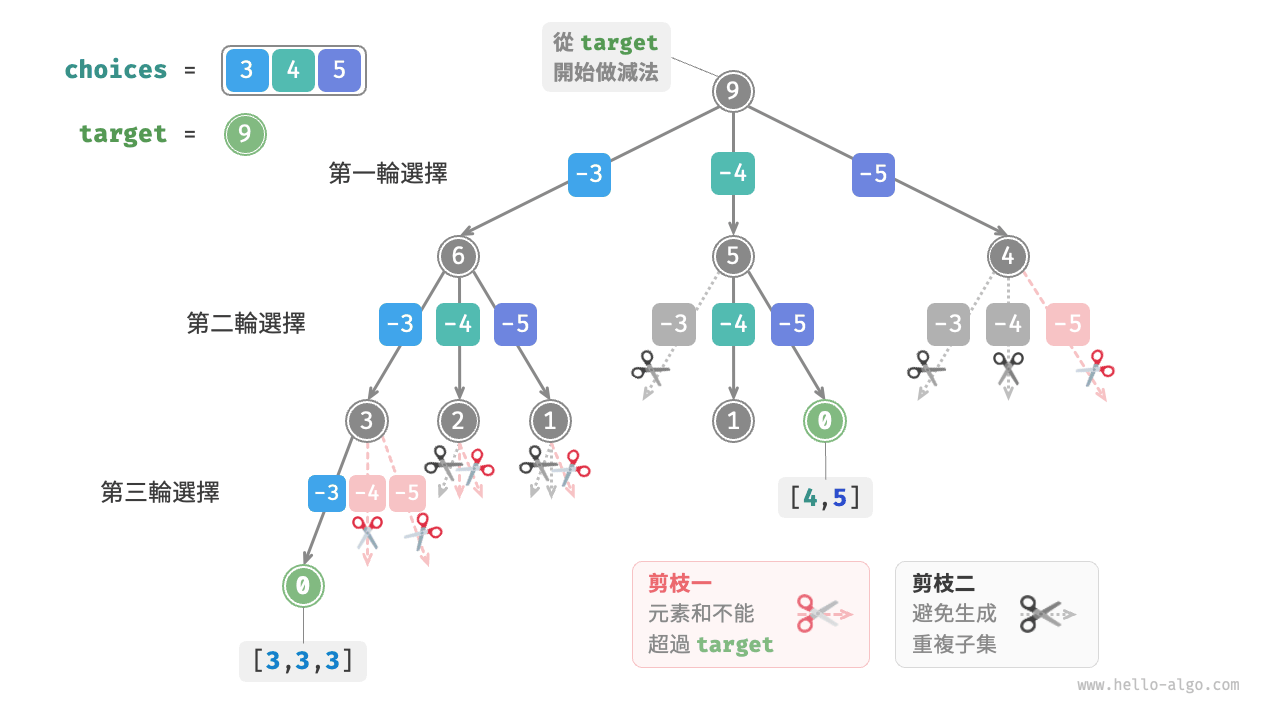
這是因為搜尋過程是區分選擇順序的，然而子集不區分選擇順序。如圖 13-10 所示，先選 \(4\) 後選 \(5\) 與先選 \(5\) 後選 \(4\) 是不同的分支，但對應同一個子集。

圖 13-10   子集搜尋與越界剪枝

為了去除重複子集，一種直接的思路是對結果串列進行去重。但這個方法效率很低，有兩方面原因。

• 當陣列元素較多，尤其是當 target 較大時，搜尋過程會產生大量的重複子集。
• 比較子集（陣列）的異同非常耗時，需要先排序陣列，再比較陣列中每個元素的異同。

2.   重複子集剪枝

我們考慮在搜尋過程中透過剪枝進行去重。觀察圖 13-11 ，重複子集是在以不同順序選擇陣列元素時產生的，例如以下情況。

1. 當第一輪和第二輪分別選擇 \(3\) 和 \(4\) 時，會生成包含這兩個元素的所有子集，記為 \([3, 4, \dots]\) 。
2. 之後，當第一輪選擇 \(4\) 時，則第二輪應該跳過 \(3\) ，因為該選擇產生的子集 \([4, 3, \dots]\) 和第 1. 步中生成的子集完全重複。

在搜尋過程中，每一層的選擇都是從左到右被逐個嘗試的，因此越靠右的分支被剪掉的越多。

1. 前兩輪選擇 \(3\) 和 \(5\) ，生成子集 \([3, 5, \dots]\) 。
2. 前兩輪選擇 \(4\) 和 \(5\) ，生成子集 \([4, 5, \dots]\) 。
3. 若第一輪選擇 \(5\) ，則第二輪應該跳過 \(3\) 和 \(4\) ，因為子集 \([5, 3, \dots]\) 和 \([5, 4, \dots]\) 與第 1. 步和第 2. 步中描述的子集完全重複。

圖 13-11   不同選擇順序導致的重複子集

總結來看，給定輸入陣列 \([x_1, x_2, \dots, x_n]\) ，設搜尋過程中的選擇序列為 \([x_{i_1}, x_{i_2}, \dots, x_{i_m}]\) ，則該選擇序列需要滿足 \(i_1 \leq i_2 \leq \dots \leq i_m\) ，不滿足該條件的選擇序列都會造成重複，應當剪枝。

3.   程式碼實現

為實現該剪枝，我們初始化變數 start ，用於指示走訪起始點。當做出選擇 \(x_{i}\) 後，設定下一輪從索引 \(i\) 開始走訪。這樣做就可以讓選擇序列滿足 \(i_1 \leq i_2 \leq \dots \leq i_m\) ，從而保證子集唯一。

除此之外，我們還對程式碼進行了以下兩項最佳化。

• 在開啟搜尋前，先將陣列 nums 排序。在走訪所有選擇時，當子集和超過 target 時直接結束迴圈，因為後邊的元素更大，其子集和一定超過 target 。
• 省去元素和變數 total ，透過在 target 上執行減法來統計元素和，當 target 等於 \(0\) 時記錄解。

PythonC++JavaC#GoSwiftJSTSDartRustCKotlinRubyZig

subset_sum_i.py

def backtrack(
    state: list[int], target: int, choices: list[int], start: int, res: list[list[int]]
):
    """回溯演算法：子集和 I"""
    # 子集和等於 target 時，記錄解
    if target == 0:
        res.append(list(state))
        return
    # 走訪所有選擇
    # 剪枝二：從 start 開始走訪，避免生成重複子集
    for i in range(start, len(choices)):
        # 剪枝一：若子集和超過 target ，則直接結束迴圈
        # 這是因為陣列已排序，後邊元素更大，子集和一定超過 target
        if target - choices[i] < 0:
            break
        # 嘗試：做出選擇，更新 target, start
        state.append(choices[i])
        # 進行下一輪選擇
        backtrack(state, target - choices[i], choices, i, res)
        # 回退：撤銷選擇，恢復到之前的狀態
        state.pop()

def subset_sum_i(nums: list[int], target: int) -> list[list[int]]:
    """求解子集和 I"""
    state = []  # 狀態（子集）
    nums.sort()  # 對 nums 進行排序
    start = 0  # 走訪起始點
    res = []  # 結果串列（子集串列）
    backtrack(state, target, nums, start, res)
    return res

subset_sum_i.cpp

/* 回溯演算法：子集和 I */
void backtrack(vector<int> &state, int target, vector<int> &choices, int start, vector<vector<int>> &res) {
    // 子集和等於 target 時，記錄解
    if (target == 0) {
        res.push_back(state);
        return;
    }
    // 走訪所有選擇
    // 剪枝二：從 start 開始走訪，避免生成重複子集
    for (int i = start; i < choices.size(); i++) {
        // 剪枝一：若子集和超過 target ，則直接結束迴圈
        // 這是因為陣列已排序，後邊元素更大，子集和一定超過 target
        if (target - choices[i] < 0) {
            break;
        }
        // 嘗試：做出選擇，更新 target, start
        state.push_back(choices[i]);
        // 進行下一輪選擇
        backtrack(state, target - choices[i], choices, i, res);
        // 回退：撤銷選擇，恢復到之前的狀態
        state.pop_back();
    }
}

/* 求解子集和 I */
vector<vector<int>> subsetSumI(vector<int> &nums, int target) {
    vector<int> state;              // 狀態（子集）
    sort(nums.begin(), nums.end()); // 對 nums 進行排序
    int start = 0;                  // 走訪起始點
    vector<vector<int>> res;        // 結果串列（子集串列）
    backtrack(state, target, nums, start, res);
    return res;
}

subset_sum_i.java

/* 回溯演算法：子集和 I */
void backtrack(List<Integer> state, int target, int[] choices, int start, List<List<Integer>> res) {
    // 子集和等於 target 時，記錄解
    if (target == 0) {
        res.add(new ArrayList<>(state));
        return;
    }
    // 走訪所有選擇
    // 剪枝二：從 start 開始走訪，避免生成重複子集
    for (int i = start; i < choices.length; i++) {
        // 剪枝一：若子集和超過 target ，則直接結束迴圈
        // 這是因為陣列已排序，後邊元素更大，子集和一定超過 target
        if (target - choices[i] < 0) {
            break;
        }
        // 嘗試：做出選擇，更新 target, start
        state.add(choices[i]);
        // 進行下一輪選擇
        backtrack(state, target - choices[i], choices, i, res);
        // 回退：撤銷選擇，恢復到之前的狀態
        state.remove(state.size() - 1);
    }
}

/* 求解子集和 I */
List<List<Integer>> subsetSumI(int[] nums, int target) {
    List<Integer> state = new ArrayList<>(); // 狀態（子集）
    Arrays.sort(nums); // 對 nums 進行排序
    int start = 0; // 走訪起始點
    List<List<Integer>> res = new ArrayList<>(); // 結果串列（子集串列）
    backtrack(state, target, nums, start, res);
    return res;
}

subset_sum_i.cs

/* 回溯演算法：子集和 I */
void Backtrack(List<int> state, int target, int[] choices, int start, List<List<int>> res) {
    // 子集和等於 target 時，記錄解
    if (target == 0) {
        res.Add(new List<int>(state));
        return;
    }
    // 走訪所有選擇
    // 剪枝二：從 start 開始走訪，避免生成重複子集
    for (int i = start; i < choices.Length; i++) {
        // 剪枝一：若子集和超過 target ，則直接結束迴圈
        // 這是因為陣列已排序，後邊元素更大，子集和一定超過 target
        if (target - choices[i] < 0) {
            break;
        }
        // 嘗試：做出選擇，更新 target, start
        state.Add(choices[i]);
        // 進行下一輪選擇
        Backtrack(state, target - choices[i], choices, i, res);
        // 回退：撤銷選擇，恢復到之前的狀態
        state.RemoveAt(state.Count - 1);
    }
}

/* 求解子集和 I */
List<List<int>> SubsetSumI(int[] nums, int target) {
    List<int> state = []; // 狀態（子集）
    Array.Sort(nums); // 對 nums 進行排序
    int start = 0; // 走訪起始點
    List<List<int>> res = []; // 結果串列（子集串列）
    Backtrack(state, target, nums, start, res);
    return res;
}

subset_sum_i.go

/* 回溯演算法：子集和 I */
func backtrackSubsetSumI(start, target int, state, choices *[]int, res *[][]int) {
    // 子集和等於 target 時，記錄解
    if target == 0 {
        newState := append([]int{}, *state...)
        *res = append(*res, newState)
        return
    }
    // 走訪所有選擇
    // 剪枝二：從 start 開始走訪，避免生成重複子集
    for i := start; i < len(*choices); i++ {
        // 剪枝一：若子集和超過 target ，則直接結束迴圈
        // 這是因為陣列已排序，後邊元素更大，子集和一定超過 target
        if target-(*choices)[i] < 0 {
            break
        }
        // 嘗試：做出選擇，更新 target, start
        *state = append(*state, (*choices)[i])
        // 進行下一輪選擇
        backtrackSubsetSumI(i, target-(*choices)[i], state, choices, res)
        // 回退：撤銷選擇，恢復到之前的狀態
        *state = (*state)[:len(*state)-1]
    }
}

/* 求解子集和 I */
func subsetSumI(nums []int, target int) [][]int {
    state := make([]int, 0) // 狀態（子集）
    sort.Ints(nums)         // 對 nums 進行排序
    start := 0              // 走訪起始點
    res := make([][]int, 0) // 結果串列（子集串列）
    backtrackSubsetSumI(start, target, &state, &nums, &res)
    return res
}

subset_sum_i.swift

/* 回溯演算法：子集和 I */
func backtrack(state: inout [Int], target: Int, choices: [Int], start: Int, res: inout [[Int]]) {
    // 子集和等於 target 時，記錄解
    if target == 0 {
        res.append(state)
        return
    }
    // 走訪所有選擇
    // 剪枝二：從 start 開始走訪，避免生成重複子集
    for i in choices.indices.dropFirst(start) {
        // 剪枝一：若子集和超過 target ，則直接結束迴圈
        // 這是因為陣列已排序，後邊元素更大，子集和一定超過 target
        if target - choices[i] < 0 {
            break
        }
        // 嘗試：做出選擇，更新 target, start
        state.append(choices[i])
        // 進行下一輪選擇
        backtrack(state: &state, target: target - choices[i], choices: choices, start: i, res: &res)
        // 回退：撤銷選擇，恢復到之前的狀態
        state.removeLast()
    }
}

/* 求解子集和 I */
func subsetSumI(nums: [Int], target: Int) -> [[Int]] {
    var state: [Int] = [] // 狀態（子集）
    let nums = nums.sorted() // 對 nums 進行排序
    let start = 0 // 走訪起始點
    var res: [[Int]] = [] // 結果串列（子集串列）
    backtrack(state: &state, target: target, choices: nums, start: start, res: &res)
    return res
}

subset_sum_i.js

/* 回溯演算法：子集和 I */
function backtrack(state, target, choices, start, res) {
    // 子集和等於 target 時，記錄解
    if (target === 0) {
        res.push([...state]);
        return;
    }
    // 走訪所有選擇
    // 剪枝二：從 start 開始走訪，避免生成重複子集
    for (let i = start; i < choices.length; i++) {
        // 剪枝一：若子集和超過 target ，則直接結束迴圈
        // 這是因為陣列已排序，後邊元素更大，子集和一定超過 target
        if (target - choices[i] < 0) {
            break;
        }
        // 嘗試：做出選擇，更新 target, start
        state.push(choices[i]);
        // 進行下一輪選擇
        backtrack(state, target - choices[i], choices, i, res);
        // 回退：撤銷選擇，恢復到之前的狀態
        state.pop();
    }
}

/* 求解子集和 I */
function subsetSumI(nums, target) {
    const state = []; // 狀態（子集）
    nums.sort((a, b) => a - b); // 對 nums 進行排序
    const start = 0; // 走訪起始點
    const res = []; // 結果串列（子集串列）
    backtrack(state, target, nums, start, res);
    return res;
}

subset_sum_i.ts

/* 回溯演算法：子集和 I */
function backtrack(
    state: number[],
    target: number,
    choices: number[],
    start: number,
    res: number[][]
): void {
    // 子集和等於 target 時，記錄解
    if (target === 0) {
        res.push([...state]);
        return;
    }
    // 走訪所有選擇
    // 剪枝二：從 start 開始走訪，避免生成重複子集
    for (let i = start; i < choices.length; i++) {
        // 剪枝一：若子集和超過 target ，則直接結束迴圈
        // 這是因為陣列已排序，後邊元素更大，子集和一定超過 target
        if (target - choices[i] < 0) {
            break;
        }
        // 嘗試：做出選擇，更新 target, start
        state.push(choices[i]);
        // 進行下一輪選擇
        backtrack(state, target - choices[i], choices, i, res);
        // 回退：撤銷選擇，恢復到之前的狀態
        state.pop();
    }
}

/* 求解子集和 I */
function subsetSumI(nums: number[], target: number): number[][] {
    const state = []; // 狀態（子集）
    nums.sort((a, b) => a - b); // 對 nums 進行排序
    const start = 0; // 走訪起始點
    const res = []; // 結果串列（子集串列）
    backtrack(state, target, nums, start, res);
    return res;
}

subset_sum_i.dart

/* 回溯演算法：子集和 I */
void backtrack(
  List<int> state,
  int target,
  List<int> choices,
  int start,
  List<List<int>> res,
) {
  // 子集和等於 target 時，記錄解
  if (target == 0) {
    res.add(List.from(state));
    return;
  }
  // 走訪所有選擇
  // 剪枝二：從 start 開始走訪，避免生成重複子集
  for (int i = start; i < choices.length; i++) {
    // 剪枝一：若子集和超過 target ，則直接結束迴圈
    // 這是因為陣列已排序，後邊元素更大，子集和一定超過 target
    if (target - choices[i] < 0) {
      break;
    }
    // 嘗試：做出選擇，更新 target, start
    state.add(choices[i]);
    // 進行下一輪選擇
    backtrack(state, target - choices[i], choices, i, res);
    // 回退：撤銷選擇，恢復到之前的狀態
    state.removeLast();
  }
}

/* 求解子集和 I */
List<List<int>> subsetSumI(List<int> nums, int target) {
  List<int> state = []; // 狀態（子集）
  nums.sort(); // 對 nums 進行排序
  int start = 0; // 走訪起始點
  List<List<int>> res = []; // 結果串列（子集串列）
  backtrack(state, target, nums, start, res);
  return res;
}

subset_sum_i.rs

/* 回溯演算法：子集和 I */
fn backtrack(
    mut state: Vec<i32>,
    target: i32,
    choices: &[i32],
    start: usize,
    res: &mut Vec<Vec<i32>>,
) {
    // 子集和等於 target 時，記錄解
    if target == 0 {
        res.push(state);
        return;
    }
    // 走訪所有選擇
    // 剪枝二：從 start 開始走訪，避免生成重複子集
    for i in start..choices.len() {
        // 剪枝一：若子集和超過 target ，則直接結束迴圈
        // 這是因為陣列已排序，後邊元素更大，子集和一定超過 target
        if target - choices[i] < 0 {
            break;
        }
        // 嘗試：做出選擇，更新 target, start
        state.push(choices[i]);
        // 進行下一輪選擇
        backtrack(state.clone(), target - choices[i], choices, i, res);
        // 回退：撤銷選擇，恢復到之前的狀態
        state.pop();
    }
}

/* 求解子集和 I */
fn subset_sum_i(nums: &mut [i32], target: i32) -> Vec<Vec<i32>> {
    let state = Vec::new(); // 狀態（子集）
    nums.sort(); // 對 nums 進行排序
    let start = 0; // 走訪起始點
    let mut res = Vec::new(); // 結果串列（子集串列）
    backtrack(state, target, nums, start, &mut res);
    res
}

subset_sum_i.c

/* 回溯演算法：子集和 I */
void backtrack(int target, int *choices, int choicesSize, int start) {
    // 子集和等於 target 時，記錄解
    if (target == 0) {
        for (int i = 0; i < stateSize; ++i) {
            res[resSize][i] = state[i];
        }
        resColSizes[resSize++] = stateSize;
        return;
    }
    // 走訪所有選擇
    // 剪枝二：從 start 開始走訪，避免生成重複子集
    for (int i = start; i < choicesSize; i++) {
        // 剪枝一：若子集和超過 target ，則直接結束迴圈
        // 這是因為陣列已排序，後邊元素更大，子集和一定超過 target
        if (target - choices[i] < 0) {
            break;
        }
        // 嘗試：做出選擇，更新 target, start
        state[stateSize] = choices[i];
        stateSize++;
        // 進行下一輪選擇
        backtrack(target - choices[i], choices, choicesSize, i);
        // 回退：撤銷選擇，恢復到之前的狀態
        stateSize--;
    }
}

/* 求解子集和 I */
void subsetSumI(int *nums, int numsSize, int target) {
    qsort(nums, numsSize, sizeof(int), cmp); // 對 nums 進行排序
    int start = 0;                           // 走訪起始點
    backtrack(target, nums, numsSize, start);
}

subset_sum_i.kt

/* 回溯演算法：子集和 I */
fun backtrack(
    state: MutableList<Int>,
    target: Int,
    choices: IntArray,
    start: Int,
    res: MutableList<MutableList<Int>?>
) {
    // 子集和等於 target 時，記錄解
    if (target == 0) {
        res.add(state.toMutableList())
        return
    }
    // 走訪所有選擇
    // 剪枝二：從 start 開始走訪，避免生成重複子集
    for (i in start..<choices.size) {
        // 剪枝一：若子集和超過 target ，則直接結束迴圈
        // 這是因為陣列已排序，後邊元素更大，子集和一定超過 target
        if (target - choices[i] < 0) {
            break
        }
        // 嘗試：做出選擇，更新 target, start
        state.add(choices[i])
        // 進行下一輪選擇
        backtrack(state, target - choices[i], choices, i, res)
        // 回退：撤銷選擇，恢復到之前的狀態
        state.removeAt(state.size - 1)
    }
}

/* 求解子集和 I */
fun subsetSumI(nums: IntArray, target: Int): MutableList<MutableList<Int>?> {
    val state = mutableListOf<Int>() // 狀態（子集）
    nums.sort() // 對 nums 進行排序
    val start = 0 // 走訪起始點
    val res = mutableListOf<MutableList<Int>?>() // 結果串列（子集串列）
    backtrack(state, target, nums, start, res)
    return res
}

subset_sum_i.rb

[class]{}-[func]{backtrack}

[class]{}-[func]{subset_sum_i}

subset_sum_i.zig

[class]{}-[func]{backtrack}

[class]{}-[func]{subsetSumI}

視覺化執行

全螢幕觀看 >

圖 13-12 所示為將陣列 \([3, 4, 5]\) 和目標元素 \(9\) 輸入以上程式碼後的整體回溯過程。

圖 13-12   子集和 I 回溯過程

13.3.2   考慮重複元素的情況

Question

給定一個正整數陣列 nums 和一個目標正整數 target ，請找出所有可能的組合，使得組合中的元素和等於 target 。給定陣列可能包含重複元素，每個元素只可被選擇一次。請以串列形式返回這些組合，串列中不應包含重複組合。

相比於上題，本題的輸入陣列可能包含重複元素，這引入了新的問題。例如，給定陣列 \([4, \hat{4}, 5]\) 和目標元素 \(9\) ，則現有程式碼的輸出結果為 \([4, 5], [\hat{4}, 5]\) ，出現了重複子集。

造成這種重複的原因是相等元素在某輪中被多次選擇。在圖 13-13 中，第一輪共有三個選擇，其中兩個都為 \(4\) ，會產生兩個重複的搜尋分支，從而輸出重複子集；同理，第二輪的兩個 \(4\) 也會產生重複子集。

圖 13-13   相等元素導致的重複子集

1.   相等元素剪枝

為解決此問題，我們需要限制相等元素在每一輪中只能被選擇一次。實現方式比較巧妙：由於陣列是已排序的，因此相等元素都是相鄰的。這意味著在某輪選擇中，若當前元素與其左邊元素相等，則說明它已經被選擇過，因此直接跳過當前元素。

與此同時，本題規定每個陣列元素只能被選擇一次。幸運的是，我們也可以利用變數 start 來滿足該約束：當做出選擇 \(x_{i}\) 後，設定下一輪從索引 \(i + 1\) 開始向後走訪。這樣既能去除重複子集，也能避免重複選擇元素。

2.   程式碼實現

PythonC++JavaC#GoSwiftJSTSDartRustCKotlinRubyZig

subset_sum_ii.py

def backtrack(
    state: list[int], target: int, choices: list[int], start: int, res: list[list[int]]
):
    """回溯演算法：子集和 II"""
    # 子集和等於 target 時，記錄解
    if target == 0:
        res.append(list(state))
        return
    # 走訪所有選擇
    # 剪枝二：從 start 開始走訪，避免生成重複子集
    # 剪枝三：從 start 開始走訪，避免重複選擇同一元素
    for i in range(start, len(choices)):
        # 剪枝一：若子集和超過 target ，則直接結束迴圈
        # 這是因為陣列已排序，後邊元素更大，子集和一定超過 target
        if target - choices[i] < 0:
            break
        # 剪枝四：如果該元素與左邊元素相等，說明該搜尋分支重複，直接跳過
        if i > start and choices[i] == choices[i - 1]:
            continue
        # 嘗試：做出選擇，更新 target, start
        state.append(choices[i])
        # 進行下一輪選擇
        backtrack(state, target - choices[i], choices, i + 1, res)
        # 回退：撤銷選擇，恢復到之前的狀態
        state.pop()

def subset_sum_ii(nums: list[int], target: int) -> list[list[int]]:
    """求解子集和 II"""
    state = []  # 狀態（子集）
    nums.sort()  # 對 nums 進行排序
    start = 0  # 走訪起始點
    res = []  # 結果串列（子集串列）
    backtrack(state, target, nums, start, res)
    return res

subset_sum_ii.cpp

/* 回溯演算法：子集和 II */
void backtrack(vector<int> &state, int target, vector<int> &choices, int start, vector<vector<int>> &res) {
    // 子集和等於 target 時，記錄解
    if (target == 0) {
        res.push_back(state);
        return;
    }
    // 走訪所有選擇
    // 剪枝二：從 start 開始走訪，避免生成重複子集
    // 剪枝三：從 start 開始走訪，避免重複選擇同一元素
    for (int i = start; i < choices.size(); i++) {
        // 剪枝一：若子集和超過 target ，則直接結束迴圈
        // 這是因為陣列已排序，後邊元素更大，子集和一定超過 target
        if (target - choices[i] < 0) {
            break;
        }
        // 剪枝四：如果該元素與左邊元素相等，說明該搜尋分支重複，直接跳過
        if (i > start && choices[i] == choices[i - 1]) {
            continue;
        }
        // 嘗試：做出選擇，更新 target, start
        state.push_back(choices[i]);
        // 進行下一輪選擇
        backtrack(state, target - choices[i], choices, i + 1, res);
        // 回退：撤銷選擇，恢復到之前的狀態
        state.pop_back();
    }
}

/* 求解子集和 II */
vector<vector<int>> subsetSumII(vector<int> &nums, int target) {
    vector<int> state;              // 狀態（子集）
    sort(nums.begin(), nums.end()); // 對 nums 進行排序
    int start = 0;                  // 走訪起始點
    vector<vector<int>> res;        // 結果串列（子集串列）
    backtrack(state, target, nums, start, res);
    return res;
}

subset_sum_ii.java

/* 回溯演算法：子集和 II */
void backtrack(List<Integer> state, int target, int[] choices, int start, List<List<Integer>> res) {
    // 子集和等於 target 時，記錄解
    if (target == 0) {
        res.add(new ArrayList<>(state));
        return;
    }
    // 走訪所有選擇
    // 剪枝二：從 start 開始走訪，避免生成重複子集
    // 剪枝三：從 start 開始走訪，避免重複選擇同一元素
    for (int i = start; i < choices.length; i++) {
        // 剪枝一：若子集和超過 target ，則直接結束迴圈
        // 這是因為陣列已排序，後邊元素更大，子集和一定超過 target
        if (target - choices[i] < 0) {
            break;
        }
        // 剪枝四：如果該元素與左邊元素相等，說明該搜尋分支重複，直接跳過
        if (i > start && choices[i] == choices[i - 1]) {
            continue;
        }
        // 嘗試：做出選擇，更新 target, start
        state.add(choices[i]);
        // 進行下一輪選擇
        backtrack(state, target - choices[i], choices, i + 1, res);
        // 回退：撤銷選擇，恢復到之前的狀態
        state.remove(state.size() - 1);
    }
}

/* 求解子集和 II */
List<List<Integer>> subsetSumII(int[] nums, int target) {
    List<Integer> state = new ArrayList<>(); // 狀態（子集）
    Arrays.sort(nums); // 對 nums 進行排序
    int start = 0; // 走訪起始點
    List<List<Integer>> res = new ArrayList<>(); // 結果串列（子集串列）
    backtrack(state, target, nums, start, res);
    return res;
}

subset_sum_ii.cs

/* 回溯演算法：子集和 II */
void Backtrack(List<int> state, int target, int[] choices, int start, List<List<int>> res) {
    // 子集和等於 target 時，記錄解
    if (target == 0) {
        res.Add(new List<int>(state));
        return;
    }
    // 走訪所有選擇
    // 剪枝二：從 start 開始走訪，避免生成重複子集
    // 剪枝三：從 start 開始走訪，避免重複選擇同一元素
    for (int i = start; i < choices.Length; i++) {
        // 剪枝一：若子集和超過 target ，則直接結束迴圈
        // 這是因為陣列已排序，後邊元素更大，子集和一定超過 target
        if (target - choices[i] < 0) {
            break;
        }
        // 剪枝四：如果該元素與左邊元素相等，說明該搜尋分支重複，直接跳過
        if (i > start && choices[i] == choices[i - 1]) {
            continue;
        }
        // 嘗試：做出選擇，更新 target, start
        state.Add(choices[i]);
        // 進行下一輪選擇
        Backtrack(state, target - choices[i], choices, i + 1, res);
        // 回退：撤銷選擇，恢復到之前的狀態
        state.RemoveAt(state.Count - 1);
    }
}

/* 求解子集和 II */
List<List<int>> SubsetSumII(int[] nums, int target) {
    List<int> state = []; // 狀態（子集）
    Array.Sort(nums); // 對 nums 進行排序
    int start = 0; // 走訪起始點
    List<List<int>> res = []; // 結果串列（子集串列）
    Backtrack(state, target, nums, start, res);
    return res;
}

subset_sum_ii.go

/* 回溯演算法：子集和 II */
func backtrackSubsetSumII(start, target int, state, choices *[]int, res *[][]int) {
    // 子集和等於 target 時，記錄解
    if target == 0 {
        newState := append([]int{}, *state...)
        *res = append(*res, newState)
        return
    }
    // 走訪所有選擇
    // 剪枝二：從 start 開始走訪，避免生成重複子集
    // 剪枝三：從 start 開始走訪，避免重複選擇同一元素
    for i := start; i < len(*choices); i++ {
        // 剪枝一：若子集和超過 target ，則直接結束迴圈
        // 這是因為陣列已排序，後邊元素更大，子集和一定超過 target
        if target-(*choices)[i] < 0 {
            break
        }
        // 剪枝四：如果該元素與左邊元素相等，說明該搜尋分支重複，直接跳過
        if i > start && (*choices)[i] == (*choices)[i-1] {
            continue
        }
        // 嘗試：做出選擇，更新 target, start
        *state = append(*state, (*choices)[i])
        // 進行下一輪選擇
        backtrackSubsetSumII(i+1, target-(*choices)[i], state, choices, res)
        // 回退：撤銷選擇，恢復到之前的狀態
        *state = (*state)[:len(*state)-1]
    }
}

/* 求解子集和 II */
func subsetSumII(nums []int, target int) [][]int {
    state := make([]int, 0) // 狀態（子集）
    sort.Ints(nums)         // 對 nums 進行排序
    start := 0              // 走訪起始點
    res := make([][]int, 0) // 結果串列（子集串列）
    backtrackSubsetSumII(start, target, &state, &nums, &res)
    return res
}

subset_sum_ii.swift

/* 回溯演算法：子集和 II */
func backtrack(state: inout [Int], target: Int, choices: [Int], start: Int, res: inout [[Int]]) {
    // 子集和等於 target 時，記錄解
    if target == 0 {
        res.append(state)
        return
    }
    // 走訪所有選擇
    // 剪枝二：從 start 開始走訪，避免生成重複子集
    // 剪枝三：從 start 開始走訪，避免重複選擇同一元素
    for i in choices.indices.dropFirst(start) {
        // 剪枝一：若子集和超過 target ，則直接結束迴圈
        // 這是因為陣列已排序，後邊元素更大，子集和一定超過 target
        if target - choices[i] < 0 {
            break
        }
        // 剪枝四：如果該元素與左邊元素相等，說明該搜尋分支重複，直接跳過
        if i > start, choices[i] == choices[i - 1] {
            continue
        }
        // 嘗試：做出選擇，更新 target, start
        state.append(choices[i])
        // 進行下一輪選擇
        backtrack(state: &state, target: target - choices[i], choices: choices, start: i + 1, res: &res)
        // 回退：撤銷選擇，恢復到之前的狀態
        state.removeLast()
    }
}

/* 求解子集和 II */
func subsetSumII(nums: [Int], target: Int) -> [[Int]] {
    var state: [Int] = [] // 狀態（子集）
    let nums = nums.sorted() // 對 nums 進行排序
    let start = 0 // 走訪起始點
    var res: [[Int]] = [] // 結果串列（子集串列）
    backtrack(state: &state, target: target, choices: nums, start: start, res: &res)
    return res
}

subset_sum_ii.js

/* 回溯演算法：子集和 II */
function backtrack(state, target, choices, start, res) {
    // 子集和等於 target 時，記錄解
    if (target === 0) {
        res.push([...state]);
        return;
    }
    // 走訪所有選擇
    // 剪枝二：從 start 開始走訪，避免生成重複子集
    // 剪枝三：從 start 開始走訪，避免重複選擇同一元素
    for (let i = start; i < choices.length; i++) {
        // 剪枝一：若子集和超過 target ，則直接結束迴圈
        // 這是因為陣列已排序，後邊元素更大，子集和一定超過 target
        if (target - choices[i] < 0) {
            break;
        }
        // 剪枝四：如果該元素與左邊元素相等，說明該搜尋分支重複，直接跳過
        if (i > start && choices[i] === choices[i - 1]) {
            continue;
        }
        // 嘗試：做出選擇，更新 target, start
        state.push(choices[i]);
        // 進行下一輪選擇
        backtrack(state, target - choices[i], choices, i + 1, res);
        // 回退：撤銷選擇，恢復到之前的狀態
        state.pop();
    }
}

/* 求解子集和 II */
function subsetSumII(nums, target) {
    const state = []; // 狀態（子集）
    nums.sort((a, b) => a - b); // 對 nums 進行排序
    const start = 0; // 走訪起始點
    const res = []; // 結果串列（子集串列）
    backtrack(state, target, nums, start, res);
    return res;
}

subset_sum_ii.ts

/* 回溯演算法：子集和 II */
function backtrack(
    state: number[],
    target: number,
    choices: number[],
    start: number,
    res: number[][]
): void {
    // 子集和等於 target 時，記錄解
    if (target === 0) {
        res.push([...state]);
        return;
    }
    // 走訪所有選擇
    // 剪枝二：從 start 開始走訪，避免生成重複子集
    // 剪枝三：從 start 開始走訪，避免重複選擇同一元素
    for (let i = start; i < choices.length; i++) {
        // 剪枝一：若子集和超過 target ，則直接結束迴圈
        // 這是因為陣列已排序，後邊元素更大，子集和一定超過 target
        if (target - choices[i] < 0) {
            break;
        }
        // 剪枝四：如果該元素與左邊元素相等，說明該搜尋分支重複，直接跳過
        if (i > start && choices[i] === choices[i - 1]) {
            continue;
        }
        // 嘗試：做出選擇，更新 target, start
        state.push(choices[i]);
        // 進行下一輪選擇
        backtrack(state, target - choices[i], choices, i + 1, res);
        // 回退：撤銷選擇，恢復到之前的狀態
        state.pop();
    }
}

/* 求解子集和 II */
function subsetSumII(nums: number[], target: number): number[][] {
    const state = []; // 狀態（子集）
    nums.sort((a, b) => a - b); // 對 nums 進行排序
    const start = 0; // 走訪起始點
    const res = []; // 結果串列（子集串列）
    backtrack(state, target, nums, start, res);
    return res;
}

subset_sum_ii.dart

/* 回溯演算法：子集和 II */
void backtrack(
  List<int> state,
  int target,
  List<int> choices,
  int start,
  List<List<int>> res,
) {
  // 子集和等於 target 時，記錄解
  if (target == 0) {
    res.add(List.from(state));
    return;
  }
  // 走訪所有選擇
  // 剪枝二：從 start 開始走訪，避免生成重複子集
  // 剪枝三：從 start 開始走訪，避免重複選擇同一元素
  for (int i = start; i < choices.length; i++) {
    // 剪枝一：若子集和超過 target ，則直接結束迴圈
    // 這是因為陣列已排序，後邊元素更大，子集和一定超過 target
    if (target - choices[i] < 0) {
      break;
    }
    // 剪枝四：如果該元素與左邊元素相等，說明該搜尋分支重複，直接跳過
    if (i > start && choices[i] == choices[i - 1]) {
      continue;
    }
    // 嘗試：做出選擇，更新 target, start
    state.add(choices[i]);
    // 進行下一輪選擇
    backtrack(state, target - choices[i], choices, i + 1, res);
    // 回退：撤銷選擇，恢復到之前的狀態
    state.removeLast();
  }
}

/* 求解子集和 II */
List<List<int>> subsetSumII(List<int> nums, int target) {
  List<int> state = []; // 狀態（子集）
  nums.sort(); // 對 nums 進行排序
  int start = 0; // 走訪起始點
  List<List<int>> res = []; // 結果串列（子集串列）
  backtrack(state, target, nums, start, res);
  return res;
}

subset_sum_ii.rs

/* 回溯演算法：子集和 II */
fn backtrack(
    mut state: Vec<i32>,
    target: i32,
    choices: &[i32],
    start: usize,
    res: &mut Vec<Vec<i32>>,
) {
    // 子集和等於 target 時，記錄解
    if target == 0 {
        res.push(state);
        return;
    }
    // 走訪所有選擇
    // 剪枝二：從 start 開始走訪，避免生成重複子集
    // 剪枝三：從 start 開始走訪，避免重複選擇同一元素
    for i in start..choices.len() {
        // 剪枝一：若子集和超過 target ，則直接結束迴圈
        // 這是因為陣列已排序，後邊元素更大，子集和一定超過 target
        if target - choices[i] < 0 {
            break;
        }
        // 剪枝四：如果該元素與左邊元素相等，說明該搜尋分支重複，直接跳過
        if i > start && choices[i] == choices[i - 1] {
            continue;
        }
        // 嘗試：做出選擇，更新 target, start
        state.push(choices[i]);
        // 進行下一輪選擇
        backtrack(state.clone(), target - choices[i], choices, i, res);
        // 回退：撤銷選擇，恢復到之前的狀態
        state.pop();
    }
}

/* 求解子集和 II */
fn subset_sum_ii(nums: &mut [i32], target: i32) -> Vec<Vec<i32>> {
    let state = Vec::new(); // 狀態（子集）
    nums.sort(); // 對 nums 進行排序
    let start = 0; // 走訪起始點
    let mut res = Vec::new(); // 結果串列（子集串列）
    backtrack(state, target, nums, start, &mut res);
    res
}

subset_sum_ii.c

/* 回溯演算法：子集和 II */
void backtrack(int target, int *choices, int choicesSize, int start) {
    // 子集和等於 target 時，記錄解
    if (target == 0) {
        for (int i = 0; i < stateSize; i++) {
            res[resSize][i] = state[i];
        }
        resColSizes[resSize++] = stateSize;
        return;
    }
    // 走訪所有選擇
    // 剪枝二：從 start 開始走訪，避免生成重複子集
    // 剪枝三：從 start 開始走訪，避免重複選擇同一元素
    for (int i = start; i < choicesSize; i++) {
        // 剪枝一：若子集和超過 target ，則直接跳過
        if (target - choices[i] < 0) {
            continue;
        }
        // 剪枝四：如果該元素與左邊元素相等，說明該搜尋分支重複，直接跳過
        if (i > start && choices[i] == choices[i - 1]) {
            continue;
        }
        // 嘗試：做出選擇，更新 target, start
        state[stateSize] = choices[i];
        stateSize++;
        // 進行下一輪選擇
        backtrack(target - choices[i], choices, choicesSize, i + 1);
        // 回退：撤銷選擇，恢復到之前的狀態
        stateSize--;
    }
}

/* 求解子集和 II */
void subsetSumII(int *nums, int numsSize, int target) {
    // 對 nums 進行排序
    qsort(nums, numsSize, sizeof(int), cmp);
    // 開始回溯
    backtrack(target, nums, numsSize, 0);
}

subset_sum_ii.kt

/* 回溯演算法：子集和 II */
fun backtrack(
    state: MutableList<Int>,
    target: Int,
    choices: IntArray,
    start: Int,
    res: MutableList<MutableList<Int>?>
) {
    // 子集和等於 target 時，記錄解
    if (target == 0) {
        res.add(state.toMutableList())
        return
    }
    // 走訪所有選擇
    // 剪枝二：從 start 開始走訪，避免生成重複子集
    // 剪枝三：從 start 開始走訪，避免重複選擇同一元素
    for (i in start..<choices.size) {
        // 剪枝一：若子集和超過 target ，則直接結束迴圈
        // 這是因為陣列已排序，後邊元素更大，子集和一定超過 target
        if (target - choices[i] < 0) {
            break
        }
        // 剪枝四：如果該元素與左邊元素相等，說明該搜尋分支重複，直接跳過
        if (i > start && choices[i] == choices[i - 1]) {
            continue
        }
        // 嘗試：做出選擇，更新 target, start
        state.add(choices[i])
        // 進行下一輪選擇
        backtrack(state, target - choices[i], choices, i + 1, res)
        // 回退：撤銷選擇，恢復到之前的狀態
        state.removeAt(state.size - 1)
    }
}

/* 求解子集和 II */
fun subsetSumII(nums: IntArray, target: Int): MutableList<MutableList<Int>?> {
    val state = mutableListOf<Int>() // 狀態（子集）
    nums.sort() // 對 nums 進行排序
    val start = 0 // 走訪起始點
    val res = mutableListOf<MutableList<Int>?>() // 結果串列（子集串列）
    backtrack(state, target, nums, start, res)
    return res
}

subset_sum_ii.rb

[class]{}-[func]{backtrack}

[class]{}-[func]{subset_sum_ii}

subset_sum_ii.zig

[class]{}-[func]{backtrack}

[class]{}-[func]{subsetSumII}

視覺化執行

全螢幕觀看 >

圖 13-14 展示了陣列 \([4, 4, 5]\) 和目標元素 \(9\) 的回溯過程，共包含四種剪枝操作。請你將圖示與程式碼註釋相結合，理解整個搜尋過程，以及每種剪枝操作是如何工作的。

圖 13-14   子集和 II 回溯過程