15.2 Fractional knapsack problem¶
Question
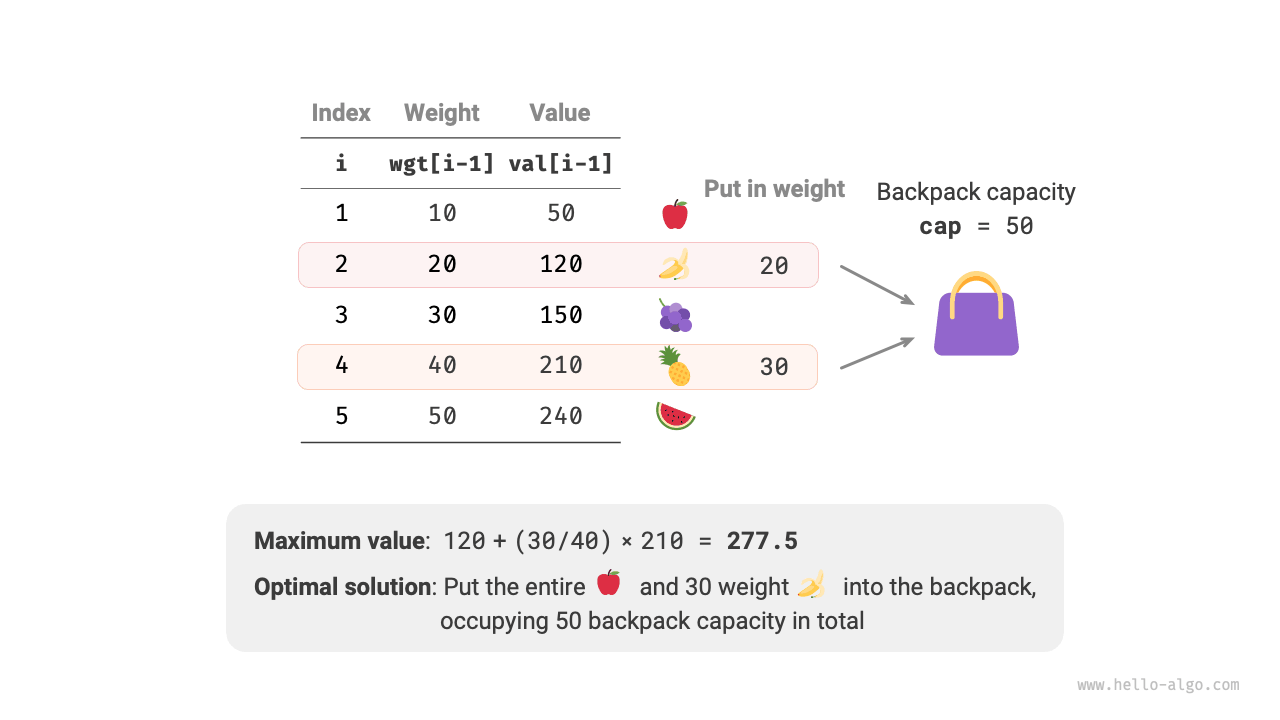
Given \(n\) items, the weight of the \(i\)-th item is \(wgt[i-1]\) and its value is \(val[i-1]\), and a knapsack with a capacity of \(cap\). Each item can be chosen only once, but a part of the item can be selected, with its value calculated based on the proportion of the weight chosen, what is the maximum value of the items in the knapsack under the limited capacity? An example is shown in Figure 15-3.
Figure 15-3 Example data of the fractional knapsack problem
The fractional knapsack problem is very similar overall to the 0-1 knapsack problem, involving the current item \(i\) and capacity \(c\), aiming to maximize the value within the limited capacity of the knapsack.
The difference is that, in this problem, only a part of an item can be chosen. As shown in Figure 15-4, we can arbitrarily split the items and calculate the corresponding value based on the weight proportion.
- For item \(i\), its value per unit weight is \(val[i-1] / wgt[i-1]\), referred to as the unit value.
- Suppose we put a part of item \(i\) with weight \(w\) into the knapsack, then the value added to the knapsack is \(w \times val[i-1] / wgt[i-1]\).
Figure 15-4 Value per unit weight of the item
1. Greedy strategy determination¶
Maximizing the total value of the items in the knapsack essentially means maximizing the value per unit weight. From this, the greedy strategy shown in Figure 15-5 can be deduced.
- Sort the items by their unit value from high to low.
- Iterate over all items, greedily choosing the item with the highest unit value in each round.
- If the remaining capacity of the knapsack is insufficient, use part of the current item to fill the knapsack.
Figure 15-5 Greedy strategy of the fractional knapsack problem
2. Code implementation¶
We have created an Item class in order to sort the items by their unit value. We loop and make greedy choices until the knapsack is full, then exit and return the solution:
class Item:
"""Item"""
def __init__(self, w: int, v: int):
self.w = w # Item weight
self.v = v # Item value
def fractional_knapsack(wgt: list[int], val: list[int], cap: int) -> int:
"""Fractional knapsack: Greedy"""
# Create an item list, containing two properties: weight, value
items = [Item(w, v) for w, v in zip(wgt, val)]
# Sort by unit value item.v / item.w from high to low
items.sort(key=lambda item: item.v / item.w, reverse=True)
# Loop for greedy selection
res = 0
for item in items:
if item.w <= cap:
# If the remaining capacity is sufficient, put the entire item into the knapsack
res += item.v
cap -= item.w
else:
# If the remaining capacity is insufficient, put part of the item into the knapsack
res += (item.v / item.w) * cap
# No remaining capacity left, thus break the loop
break
return res
/* Item */
class Item {
int w; // Item weight
int v; // Item value
public Item(int w, int v) {
this.w = w;
this.v = v;
}
}
/* Fractional knapsack: Greedy */
double fractionalKnapsack(int[] wgt, int[] val, int cap) {
// Create an item list, containing two properties: weight, value
Item[] items = new Item[wgt.length];
for (int i = 0; i < wgt.length; i++) {
items[i] = new Item(wgt[i], val[i]);
}
// Sort by unit value item.v / item.w from high to low
Arrays.sort(items, Comparator.comparingDouble(item -> -((double) item.v / item.w)));
// Loop for greedy selection
double res = 0;
for (Item item : items) {
if (item.w <= cap) {
// If the remaining capacity is sufficient, put the entire item into the knapsack
res += item.v;
cap -= item.w;
} else {
// If the remaining capacity is insufficient, put part of the item into the knapsack
res += (double) item.v / item.w * cap;
// No remaining capacity left, thus break the loop
break;
}
}
return res;
}
Apart from sorting, in the worst case, the entire list of items needs to be traversed, hence the time complexity is \(O(n)\), where \(n\) is the number of items.
Since an Item object list is initialized, the space complexity is \(O(n)\).
3. Correctness proof¶
Using proof by contradiction. Suppose item \(x\) has the highest unit value, and some algorithm yields a maximum value res, but the solution does not include item \(x\).
Now remove a unit weight of any item from the knapsack and replace it with a unit weight of item \(x\). Since the unit value of item \(x\) is the highest, the total value after replacement will definitely be greater than res. This contradicts the assumption that res is the optimal solution, proving that the optimal solution must include item \(x\).
For other items in this solution, we can also construct the above contradiction. Overall, items with greater unit value are always better choices, proving that the greedy strategy is effective.
As shown in Figure 15-6, if the item weight and unit value are viewed as the horizontal and vertical axes of a two-dimensional chart respectively, the fractional knapsack problem can be transformed into "seeking the largest area enclosed within a limited horizontal axis range". This analogy can help us understand the effectiveness of the greedy strategy from a geometric perspective.
Figure 15-6 Geometric representation of the fractional knapsack problem